聚类、距离衡量方法
聚类分析
一、相似性度量方法
| 欧氏距离 | 马氏距离 |
|---|---|
| 标准化欧式距离 | 海明距离 |
| 哈曼顿距离 | 杰卡德距离 |
| 切比雪夫距离 | 相关距离 |
| 闵可夫斯基距离 | 信息熵 |
| 余弦距离 | 基于核函数的度量 |
1. 欧氏距离(欧几里得距离)
两个向量 α ( x 11 , x 12 , … , x 1 n ) \alpha\left(x_{11}, x_{12}, \ldots, x_{1 n}\right) α(x11,x12,…,x1n)和 β ( x 21 , x 22 , … , x 2 n ) \beta\left(x_{21}, x_{22}, \ldots, x_{2 n}\right) β(x21,x22,…,x2n)之间的欧氏距离为:
d 12 = ∑ k = 1 n ( x 1 k − x 2 k ) 2 d_{12}=\sqrt{\sum_{k=1}^{n}\left(x_{1 k}-x_{2 k}\right)^{2}} d12=k=1∑n(x1k−x2k)2
欧式距离就是我们平时用的两点间的距离
2. 标准化欧氏距离
根据数据各维分量的分布不同将各个分量都标准化到均值、方差相等。
两个向量 α ( x 11 , x 12 , … , x 1 n ) \alpha\left(x_{11}, x_{12}, \ldots, x_{1 n}\right) α(x11,x12,…,x1n)和 β ( x 21 , x 22 , … , x 2 n ) \beta\left(x_{21}, x_{22}, \ldots, x_{2 n}\right) β(x21,x22,…,x2n)之间的欧氏距离为:
d 12 = ∑ k = 1 n ( x 1 k − x 2 k s k ) 2 d_{12}=\sqrt{\sum_{k=1}^{n}\left(\frac{x_{1 k}-x_{2 k}}{s_k}\right)^{2}} d12=k=1∑n(skx1k−x2k)2
这个 s k s_k sk是个方差,在标准化欧式距离中,方差的倒数我们可以视为一种权重,因此标准化的欧式距离也可以视为一种加权的欧式距离。
3. 曼哈顿距离
曼哈顿距离也称为L1-距离或城市距离,对于两个 n n n维向量 α , β \alpha, \beta α,β来说他们的曼哈顿距离,指的是每一个分量的差值的绝对值,然后再次求和。
两个向量 α ( x 11 , x 12 , … , x 1 n ) \alpha\left(x_{11}, x_{12}, \ldots, x_{1 n}\right) α(x11,x12,…,x1n)和 β ( x 21 , x 22 , … , x 2 n ) \beta\left(x_{21}, x_{22}, \ldots, x_{2 n}\right) β(x21,x22,…,x2n)之间的曼哈顿距离为:
d 12 = ∑ k = 1 n ∣ x 1 k − x 2 k ∣ d_{12}=\sum_{k=1}^{n}{\left | x_{1k}-x_{2k} \right | } d12=k=1∑n∣x1k−x2k∣
4. 切比雪夫距离
两个向量 α ( x 11 , x 12 , … , x 1 n ) \alpha\left(x_{11}, x_{12}, \ldots, x_{1 n}\right) α(x11,x12,…,x1n)和 β ( x 21 , x 22 , … , x 2 n ) \beta\left(x_{21}, x_{22}, \ldots, x_{2 n}\right) β(x21,x22,…,x2n)之间的切比雪夫距离为:
d 12 = max i ( ∣ x 1 i − x 2 i ∣ ) d_{12}=\max _{i}\left(\left|x_{1 i}-x_{2 i}\right|\right) d12=imax(∣x1i−x2i∣)
即,在 α , β \alpha,\beta α,β他们对应的分量的差值的绝对值当中最大的那个,就是切比雪夫距离
该公式等价于:
d 12 = lim k → ∞ ( ∑ i = 1 n ∣ x 1 i − x 2 i ∣ k ) 1 / k d_{12}=\lim _{k \rightarrow \infty}\left(\sum_{i=1}^{n}\left|x_{1 i}-x_{2 i}\right|^{k}\right)^{1 / k} d12=k→∞lim(i=1∑n∣x1i−x2i∣k)1/k
5.闵可夫斯基距离
两个向量 α ( x 11 , x 12 , … , x 1 n ) \alpha\left(x_{11}, x_{12}, \ldots, x_{1 n}\right) α(x11,x12,…,x1n)和 β ( x 21 , x 22 , … , x 2 n ) \beta\left(x_{21}, x_{22}, \ldots, x_{2 n}\right) β(x21,x22,…,x2n)之间的闵可夫斯基距离为:
d 12 = ∑ k = 1 n ( x 1 k − x 2 k ) p p d_{12}=\sqrt[p]{\sum_{k=1}^{n}\left(x_{1 k}-x_{2 k}\right)^{p}} d12=pk=1∑n(x1k−x2k)p
- p=1时,它是曼哈顿距离
- p=2时,它是欧氏距离
- p= ∞ \infin ∞时,它是切比雪夫距离
| 闵可夫斯基类的距离缺陷 |
|---|
| 举例:在a和b之间他们的身高差10公分。在a和c之间,他们的体重差10公斤。发现,实际上,两个10,他们单位是不同的,即量纲不同,不能在一起衡量。 缺陷: - 将各个分量的量纲,当做相同看待 - 没有考虑各个分量的分布(如期望、方差等)可能不同 |
6. 余弦距离
余弦距离的几何意义不仅能包含长度也包含方向。
余弦距离是度量两个向量方向差异的一种方法。
两个向量 α ( x 11 , x 12 , … , x 1 n ) \alpha\left(x_{11}, x_{12}, \ldots, x_{1 n}\right) α(x11,x12,…,x1n)和 β ( x 21 , x 22 , … , x 2 n ) \beta\left(x_{21}, x_{22}, \ldots, x_{2 n}\right) β(x21,x22,…,x2n)之间的夹角余弦度量为:
cos ( θ ) = α ⋅ β ∣ α ∣ ∣ β ∣ \cos (\theta)=\frac{\alpha \cdot \beta}{|\alpha||\beta|} cos(θ)=∣α∣∣β∣α⋅β
7. 马氏距离
马氏距离是基于样本分布的一种距离。刚才讲到的距离都是指的是两个不同的向量 α , β \alpha, \beta α,β之间一个距离的度量。
在马氏距离中,它是基于样本分布的这样一种度量方法。
它是规范化主成分空间当中的欧式距离。
| 什么是规范化主成分空间? |
|---|
| 规范化的主成分空间就是利用主成分分析对一些数据进行主成分分解,再对所有主成分分解轴做归一化,形成新的坐标轴,由这些坐标轴组成的空间就是规范化的主成分空间。 |
| 视频:用最直观的方式告诉你:什么是主成分分析PCA_哔哩哔哩_bilibili |
向量 X i , X j X_{i},X_{j} Xi,Xj之间的马氏距离为:
D ( X i , X j ) = ( X i − X j ) T S − 1 ( X i − X j ) D\left(X_{i}, X_{j}\right)=\sqrt{\left(X_{i}-X_{j}\right)^{\mathrm{T}} S^{-1}\left(X_{i}-X_{j}\right)} D(Xi,Xj)=(Xi−Xj)TS−1(Xi−Xj)
其中 S S S是协方差矩阵。
当 S S S是对角矩阵时,马氏距离就变成了标准化的欧式距离。
总结一下马氏距离的特点:
- 量纲无关
- 马氏距离的计算是建立在总体样本的基础上
- 计算马氏距离过程中,要求总体样本数大于样本的维数。
8. 海明距离
两个等长二进制字符串将其中一个变为另一个所需要的最小变换次数。
例如:字符串1111与1001之间的海明距离为2
9.杰卡德距离
杰卡德相似系数:两个集合A和B的交集元素在A、B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号 J ( A , B ) J(A, B) J(A,B)表示:
J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∪ B ∣ J(A, B)=\frac{|A \cap B|}{|A \cup B|} J(A,B)=∣A∪B∣∣A∩B∣
杰卡德距离:与杰卡德相似系数相反,用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度:
J δ ( A , B ) = 1 − J ( A , B ) = ∣ A ∪ B ∣ − ∣ A ∩ B ∣ ∣ A ∪ B ∣ J_{\delta}(A, B)=1-J(A, B)=\frac{|A \cup B|-|A \cap B|}{|A \cup B|} Jδ(A,B)=1−J(A,B)=∣A∪B∣∣A∪B∣−∣A∩B∣
10. 相关距离
相关系数:衡量随机变量 X X X与 Y Y Y相关程度的一种方法,相关系数的取值范围是 [ − 1 , 1 ] [-1, 1] [−1,1]。
ρ X Y = Cov ( X , Y ) D ( X ) D ( Y ) = E ( ( E − E X ) ( Y − E Y ) ) D ( X ) D ( Y ) \rho_{X Y}=\frac{\operatorname{Cov}(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}=\frac{E((E-E X)(Y-E Y))}{\sqrt{D(X)} \sqrt{D(Y)}} ρXY=D(X)D(Y)Cov(X,Y)=D(X)D(Y)E((E−EX)(Y−EY))
相关系数的绝对值越大,则表明 X X X与 Y Y Y相关度越高。当 X X X与 Y Y Y线性相关时,相关系数取值为1(正线性相关)或-1(负线性相关)
相关距离:
D X Y = 1 − ρ X Y D_{X Y}=1-\rho_{X Y} DXY=1−ρXY
11. 信息熵
以上的距离度量方法度量皆为两个样本(向量)之间的距离
12. 基于核函数的度量
把原始样本空间中线性不可分的数据点采用核函数映射到高维空间中使其线性可分的一种度量方法。
二、经典的聚类方法
聚类方法往往学术界对聚类算法并没有一个公共的分类方法
- 划分方法
- 经典方法:
K-means及其变种、K-中心点、CLARA、CLARANS
- 经典方法:
- 层次方法
- 基于密度方法
- 基于网络方法
- 基于模型方法
1. K-means
K-means算法流程:
- 从数据集D中随机选择K个对象作为初始簇中心
- 将每个对象分配到与其最近的簇中心的簇中
- 重新计算簇的均值,使用新的均值作为当前簇的中心
- 重复步骤2、3,直到所有簇中的对象不再变化。
K-means算法的局限性:
- 算法可能终止于局部最优解
- 算法只有当簇均值可求或可定义时才能使用
- 簇数目必须事先给定,而在一些实际应用中K是很难事先知道的
- 不适合发现非凸形状的簇,或者大小差别很大的簇
- K-means算法,对噪声和离群点的数据敏感
原因在于度量方法基于的是欧拉距离,因此,对噪声和离群点是比较敏感的。
2. K中心点算法(K-Medoide)
K-中心点算法也是一种常用的聚类算法,K-中心点聚类的基本思想和K-Means的思想相同,实质上是对K-means算法的优化和改进。在K-means中,异常数据对其的算法过程会有较大的影响。在K-means算法执行过程中,可以通过随机的方式选择初始质心,也只有初始时通过随机方式产生的质心才是实际需要聚簇集合的中心点,而后面通过不断迭代产生的新的质心很可能并不是在聚簇中的点。如果某些异常点距离质心相对较大时,很可能导致重新计算得到的质心偏离了聚簇的真实中心。
K-Medoide算法流程:
- 从数据集D中随机选择K个对象作为初始簇中心
- 计算其余所有点到K个中心点的距离,并把每个点到K个中心点最短的聚簇作为自己所属的聚簇
- 在每个聚簇中按照顺序依次选取点,计算该点到当前聚簇中所有点距离之和,最终距离之和最小的点,则视为新的中心点。
- 重复2,3步骤,直到各个聚簇的中心点不再改变。
3. 核K-means
就是将数据点都投影到了一个高维的特征空间中(为了凸显不同样本中的差异),然后再在这个高维的特征空间中,进行传统的k-means聚类。
4. EM聚类
我们知道,K-means方法是硬分聚类方法的一种。 什么是硬分聚类方法呢?就是指一个点只能属于一个簇。 EM算法,是一种软分聚类方法,这种方法,指的是每一个点, 都有属于某个簇的概率,这是硬分聚类与软分聚类不同的地方。 EM聚类是典型的软分聚类方法。
5. 谱聚类
谱聚类(spectral clustering)及其实现详解_yycc-CSDN博客_谱聚类实现
6.DBSCAN聚类
先看一些定义:
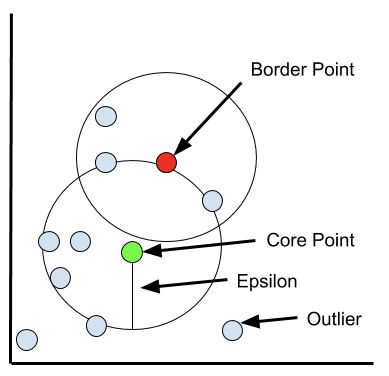
- ε \varepsilon ε邻域:以给定对象点为圆心,画一个半径为 ε \varepsilon ε的圈,圆内就是这个对象的 ε \varepsilon ε邻域。
- 核心对象:该对象的圈里,包含足够多的其他点,足够多是指至少Minpts个
- 直接密度可达:有两个点p和q,q是核心对象,p在q的圈里。那么,则称p从q出发是直接密度可达的。
- 密度可达:有个对象链,包含一堆点 p 1 , p 2 , … , p n p_1,p_2,\dots,p_n p1,p2,…,pn。
- p 2 p_2 p2直接密度可达 p 1 p_1 p1
- p 3 p_3 p3直接密度可达 p 2 p_2 p2
- p 4 p_4 p4直接密度可达 p 3 p_3 p3
- p 5 p_5 p5直接密度可达 p 4 p_4 p4
- …
- p n p_n pn直接密度可达 p n − 1 p_n-1 pn−1
- 其实这就是一个直接密度可达组成的链,我们称 p 1 p_1 p1从 p n p_n pn出发是密度可达的。
- 密度相连:核心点p的圈内存在两个点m和n,m和n就是密度相连的
DBSCAN最终的聚类状态是,所有密度可达的和密度相连的被划分到一个簇。
这有个网站,自己玩一下Visualizing DBSCAN Clustering (naftaliharris.com)