R实现几种简单的聚类分析
有句话说得好:物以类聚,人以群分;而聚类分析就是要把这样的“类”和“群”找出来。聚类分析指将物理或抽象对象的集合分组为由类似的对象组成的多个类的分析过程。比如两个人都喜欢红色的衣服、甜食、舞蹈、文学,如果从这几方面来考虑的话,我们完全有理由认为这两个人是一类人。那么当我们知道有一个人喜欢唱歌的话,根据他们是一类人的分类,同样我们有理由认为另外一个人也喜欢唱歌。
下面介绍在R中三种简单聚类分析的实现:
一、K近邻聚类
K近邻算法也称为KNN算法,像所有的机器学习算法一样,KNN算法同时需要一份训练集和一份测试集。训练集中的观测值已经用类别变量标出了类别,而测试集中的观测值则不需要标出类别变量,所以KNN算法度量测试集样本与训练集样本距离用的是非类别变量,根据距离测试样本最近的K个训练样本的类别来判断测试样本的类别。
这里用的是class包中的knn.cv()函数实现KNN聚类方法。
>library(class)
#在1~150随机取出100个互不相同的数
>sam<-sample(c(1:150),100)
#由于iris数据集有150行,前、中、后50行恰好是不同的三类,将其分别标记为0、1、2类
>iris[6]<-c(rep(0,50),rep(1,50),rep(2,50))
#iris.sam、iris.test分别表示训练集和测试集
>iris.sam<-iris[sam,]
>iris.test<-iris[-sam,]
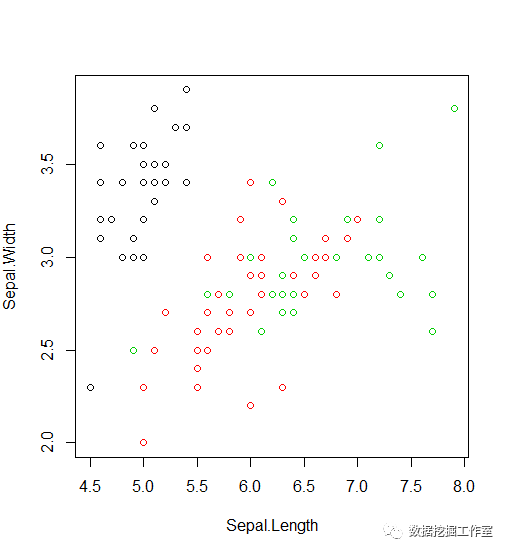
>plot(iris.sam[,1:2],col=iris.sam$Species)
用plot()函数查看训练集iris.sam样本的真实类别,第一个参数指定为对1、2列Sepal.Length、Sepal.Width作图,第二个参数指定以Species为类别变量标出散点颜色。可以看出左上角黑色部分明显在一起,但下面红色和绿色部分却混在一起,在面用KNN算法进行分类,直接给出类别号。
>kn<-knn.cv(iris.sam[,1:2],cl=iris.sam[,5],k=10)
>table(iris.sam$Species,kn)
kn
setosa versicolor virginica
setosa 28 0 0
versicolor 0 30 9
virginica 0 15 18
>plot(iris.sam[,1:2],col=kn)
为了便于查看,第一行代码将KNN模型结果赋给了kn,并使用第二行查看了iris.sam中Species变量与kn的列联表。可以看出属于setosa的28个样本未被分错,但属于versicolor的39个样本有9个被分到virginica类别中,属于virginica的33个样本有15个样本被分到versicolor类别中。准确率为1-(9+15)/100=0.76。最后一行使用查看了KNN算法的最终结果,好像比真实类别更集中,哈哈。
二、系统聚类
系统聚类又称为层次聚类法,不像KNN聚类训练样本类别给出,但系统聚类不分训练集和测试集,主要根据样本信息归纳出类别来,在模型创建完毕之前,样本类型未知。一般开始每个样本作为一类,每次将相似类合并,最终就聚为一个大类。主要有最小、最大、类平均、离差平方法度量类之间距离,类平均、离差平方法考虑了类别中的全体信息,通常效果最佳,这里用离差平方法。
下面用函数hclust()构建聚类模型。仍用上面的100条iris.sam作为原始数据。
#使用dist()函数为iris.sam的前四列创建了一个距离矩阵,第二个参数'euclidean'表示用欧氏距离度量样本间距离。
>disma<-dist(iris.sam[1:4],method = 'euclidean')
#用hclust()构建系统聚类模型,第二个参数表示使用离差平方法度量类与类之间的距离。
>clur<-hclust(d=disma,method = 'ward.D')
#画图,用iris.sam的第六列作为树状图的标签
>plot(clur,labels = iris.sam[,6])
从图中可以明显看出将这些数据分为三、四类是合理的,最好分为四类。并且labels = iris.sam[,6]使得树状图底部标注为0、1、2占的位置小尚且看不清楚,如果用Species就会完全看不清。
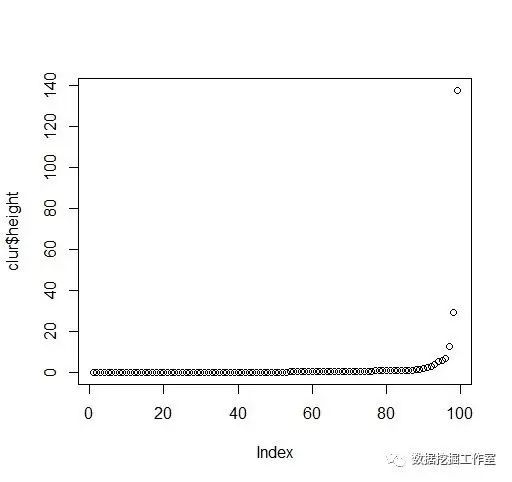
> plot(clur$height)
从碎石图可以看出有3、4个异常点,可见将iris.sam分为3、4类是合理的。
三、快速聚类
快速聚类在KNN聚类思想的基础上进一步深入得到的模型,快速聚类假设测试样本类型未知,增加了样本训练的过程。它需要手动指定样本的类别个数,首先给每个样本随机指定一个类别,然后计算自己与其它类别中心距离是否小于自己到自己类别中心距离,然后修改,不断迭代、最终一般会收敛。快速聚类的类别与初始聚类中心的选取有关,显然这样的结果一般不一样,最佳方法是多做几次快速聚类。并且当数据维数超过三维时,就不好凭画图目测大概确定出类别个数了。
R中的基础包提供了kmeans()函数用于实现快速聚类。
>kc<-kmeans(iris.sam[1:2],3)
使用iris.sam的前两列数据,指定聚类数为三类,聚类结果存放在kc中,查看kc:
K-means clustering with 3 clusters of sizes 38, 33, 29
Cluster means:
Sepal.Length Sepal.Width
1 5.768421 2.689474
2 4.969697 3.354545
3 6.806897 3.134483
Clustering vector:
80 133 100 87 138 6 84 9 122 88
1 3 1 3 3 2 1 2 1 1
38 74 41 33 85 19 53 35 25 61
2 1 2 2 1 2 3 2 2 1
7 149 68 57 123 43 78 72 90 102
2 3 1 3 3 2 3 1 1 1
139 127 115 142 86 120 113 71 8 37
1 1 1 3 1 1 3 1 2 2
3 42 140 105 109 26 125 56 132 64
2 2 3 3 3 2 3 1 3 1
60 17 50 95 144 31 28 135 134 114
1 2 2 1 3 2 2 1 1 1
146 10 143 40 14 101 15 79 45 130
3 2 1 2 2 3 2 1 2 3
30 77 121 128 99 118 52 58 13 69
2 3 3 1 1 3 3 1 2 1
81 91 108 2 27 150 97 11 93 59
1 1 3 2 2 1 1 2 1 3
70 107 82 48 116 44 145 110 66 20
1 2 1 2 3 2 3 3 3 2
Within cluster sum of squares by cluster:
[1] 7.357895 9.351515 7.384138
(between_SS / total_SS = 71.5 %)
Available components:
[1] "cluster" "centers"
[3] "totss" "withinss"
[5] "tot.withinss" "betweenss"
[7] "size" "iter"
[9] "ifault"
kc返回了每一类分别有38、33、29个样本,还返回了每一类的聚类中心,每一个样本具体属于的类,“Within cluster sum of squares by cluster:”分别显示了所有变量的离差平方差之和、每个类别所有聚类变量的离差平方差之和、每个类别所有聚类变量的离差平方差之和的和。
使用”快速聚类模型名+$+指标名称“的格式可调用快速聚类模型中的指标。
>table(iris.sam$Species,kc$cluster)
1 2 3
setosa 0 32 0
versicolor 26 0 8
virginica 12 1 2
可以看出setosa类全部分入了第二类,versicolor类型有8个分入了第三类,virginica有一个分入了第二类两个分入了第三类,快速聚类结果一般不怎么好,这里却不错哦!
>plot(iris.sam[1:2],col=kc$cluster)
这一句代码指定画图对象为iris.sam的前两列变量,第二个变量指定用kc中的cluster变量做参考为散点着色。
点击【阅读原文】,更多精彩!