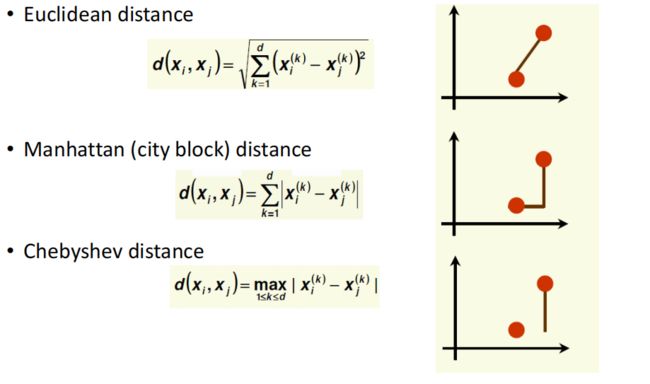
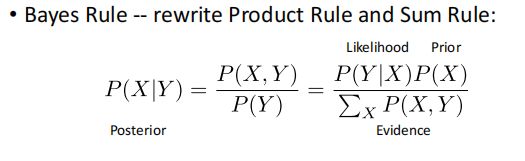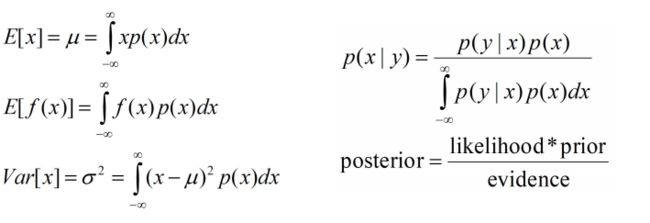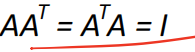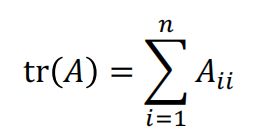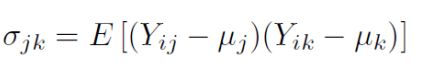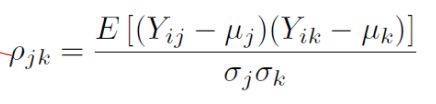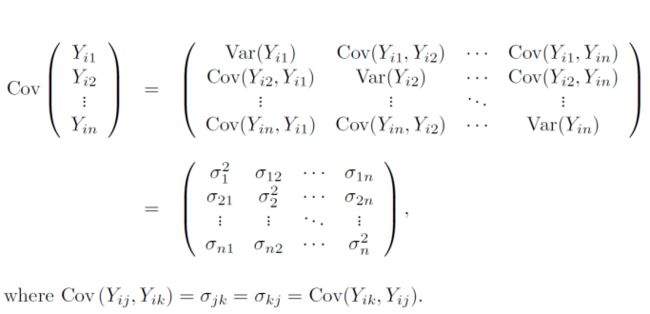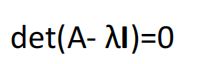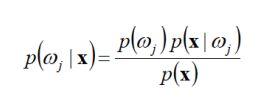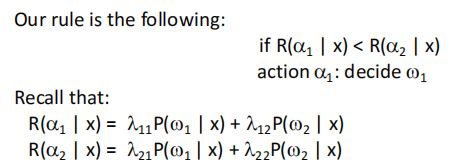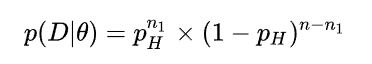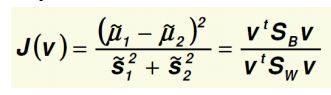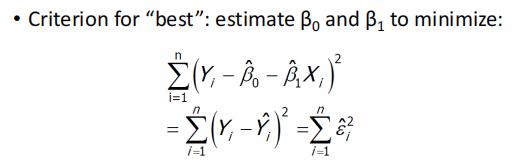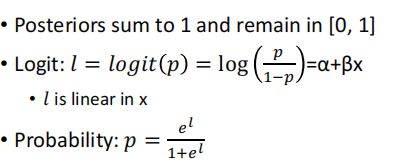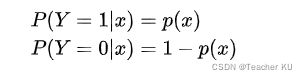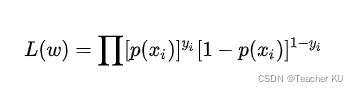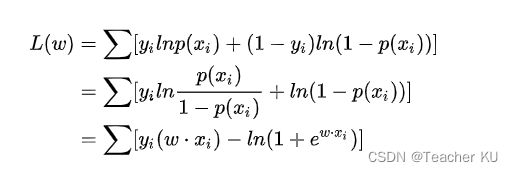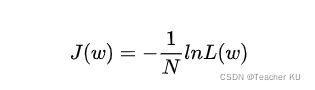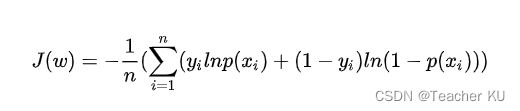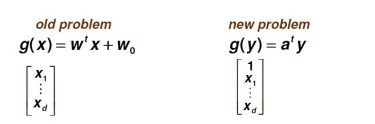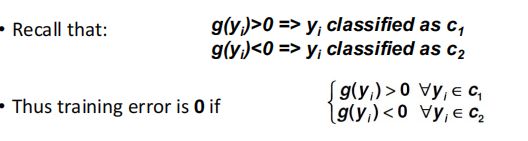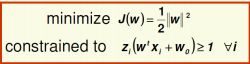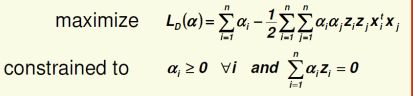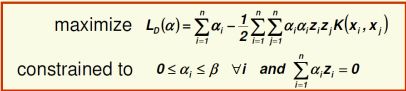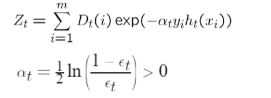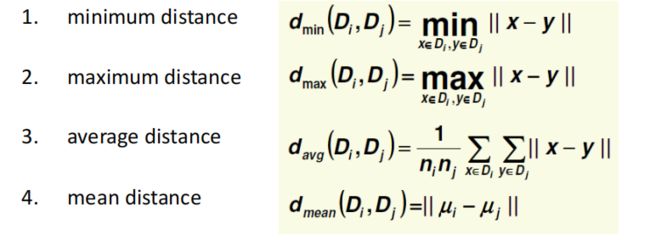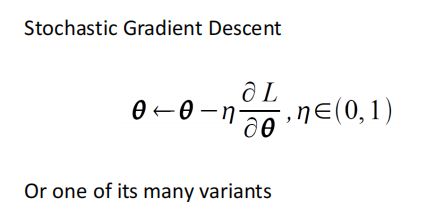EE4408: Machine Learning:
#########更新完成 ################################
更正1:MLE classifier 中是利用似然函数算出来的likehood进行判断的,MAP中才使用后验概率进行判断(Lecture 4)
更正2:LDF 打成了 LDA(Lecture 6)
更正3:LDF Criterion Function
html版本(看起来好看一点)已更新!
链接:https://pan.baidu.com/s/1borCn8R8ig04_KzHWlVE3A
提取码:pocz
希望大家考试顺利!!!!!!!!!!!!!
目录
#########更新完成 #####
EE4408: Machine Learning:
Lecture1
Types of machine learning
Probability Review
Lecture 2
Graphical Model:
Belief Networks (Bayesian Networks)
Intro to Linear Algebra:
Eigenvalue and Eigenvector
Lecture 3
Bayesian Decision Theory
MLE maximum Likelihood Estimation 极大似然估计
Lecture 4
MLE Classifier Example
Cross Validation (交叉验证)
Maximum a posteriori (MAP) Estimation
Non-parametric Classification
Dimensionality Reduction(降维)
Lecture 5
Data Scaling
Dimensionality Reduction
PCA
Eigenfaces
Lecture 6
Fisher's Linear Discriminant Analysis
LDA:Linear Discriminant Functions
Lecture 7
Linear Regression
Logistic Regression
Linear Discriminant Functions(线性判别方程)
LDF Criterion Function
Perceptron(感知机)
Non-separable Example && Convergence of Perceptron Rules
Lecture 8
Minimum Squared-Error Procedures
Support Vector Machines
SVM: Non-Separable Case
Nonlinear Mapping
Kernels(SVM的核函数)
Nonlinear SVM Step-by-Step
Multi-class SVMs
Lecture 9
Ensemble Classifiers (集成分类器)
Bagging:
Decision Tree(决策树)
Random Forest:(随机森林)
Boosting
Random Forests vs. Boosting
Lecture 10
Unsupervised Learning(Clustering)
K-means Clustering
Hierarchical Clustering(层次聚类)
Clustering Summary
Expectation Maximization
(据说不考)Lecture 11
神经网络基础知识
Perceptrons感知机
工作流程(概念)
神经网络实现流程
Some question
EE4408: Machine Learning:
Lecture1
Types of machine learning
Supervised Learning:
-
example:Regression,*Classification
-
difference: need labels,需要标签来学习
Unsupervised Learning:
-
example:Clustering
-
difference:not need labels,不需要标签进行学习
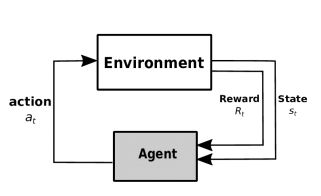
Reinforcement Learning:强化学习
-
组成部分:环境,用户
用户根据environment所处的state产生action,作用于Environment,产生reward,返回Agent,更新action产生网络,使得下一次的action会更好。
Probability Review
Discrete Random Variable:
Bayes Rule:
Continuous Random Variable:
Lecture 2
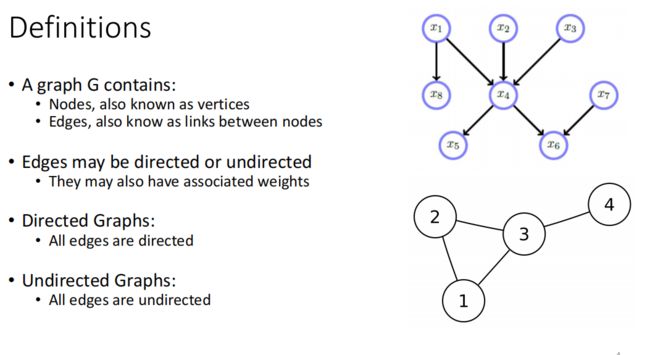
Graphical Model:
DAG:有向图,没有cycle(没有一条路径重新访问一个节点)
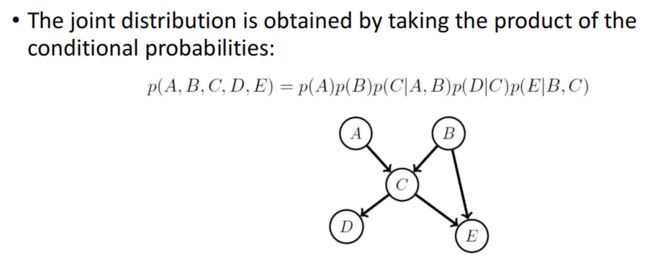
Belief Networks (Bayesian Networks)
利用给定图关系.求joint probablities
Intro to Linear Algebra:
-
Vectors:向量
-
scalars:标量
-
Subspace:子空间
-
Basis of Vector Space:基向量,在图片中,基向量为:
-
Orthogonal matrices正交矩阵,满足
-
Trace:矩阵对角线之和
-
Determinant:行列式
-
Covariance:协方差,
-
Correlation coefficient:相关系数:
-
Covariance matrix:
协方差:COV(X,Y)=E[(X-E(X))(Y-E(Y))]
-
Normal Density:正态分布
Eigenvalue and Eigenvector
用
可以求出
![]()
为Eigenvalue(特征值),
将lambda 带入
求出的x为eigenvector(特征向量)
Lecture 3
Bayesian Decision Theory
prior:先验概率 posterior:后验概率
Decision using Posteriors:
-
判断规则:
后验概率哪个大,判断成哪个
-
Error:

Error:给定x集合,后验概率是确定的,所以error就是概率小的那个
-
Loss Function
Conditional Risk:
后验概率决策的升级版,在进行决策前,设置一个参数
R()函数相当于将 每一类的错误率相加
MLE maximum Likelihood Estimation 极大似然估计
question
答案:a 因为对于每一个似然函数,都有一个确定的参数,比如高斯分布中的均值和方差,线性分类中的w和,所以他的判别函数的形状是统一的.
main idea
-
用最大似然函数渠道最大值作为估计值,就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值(模型已知,参数未知)。
-
先再写出似然函数:
-
简述方法:
Lecture 4
MLE Classifier Example
-
利用train_data 进行最大似然估计(example中估计的是var和mean)
-
利用最大似然估计的概率进行判断(更正)
-
利用测试集的标签来计算error
Cross Validation (交叉验证)
基础概念:
-
训练集(train set) —— 用于模型拟合的数据样本。
-
验证集(validation set)—— 是模型训练过程中单独留出的样本集,它可以用于调整模型的超参数和用于对模型的能力进行初步评估。 通常用来在模型迭代训练时,用以验证当前模型泛化能力(准确率,召回率等),以决定是否停止继续训练。
-
测试集 —— 用来评估模最终模型的泛化能力。但不能作为调参、选择特征等算法相关的选择的依据。
一个形象的比喻:
训练集-----------学生的课本;学生 根据课本里的内容来掌握知识。 验证集------------作业,通过作业可以知道 不同学生学习情况、进步的速度快慢。 测试集-----------考试,考的题是平常都没有见过,考察学生举一反三的能力。
K-fold cross validation
-
随机将训练数据等分成k份,S1, S2, …, Sk。
-
对于每一个模型Mi,算法执行k次,每次选择一个Sj作为验证集,而其它作为训练集来训练模型Mi,把训练得到的模型在Sj上进行测试,这样一来,每次都会得到一个误差E,最后对k次得到的误差求平均,就可以得到模型Mi的泛化误差。
-
算法选择具有最小泛化误差的模型作为最终模型,并且在整个训练集上再次训练该模型,从而得到最终的模型。
overfitting 过拟合
模型对于训练集来说太精确了,失去泛化性
Maximum a posteriori (MAP) Estimation
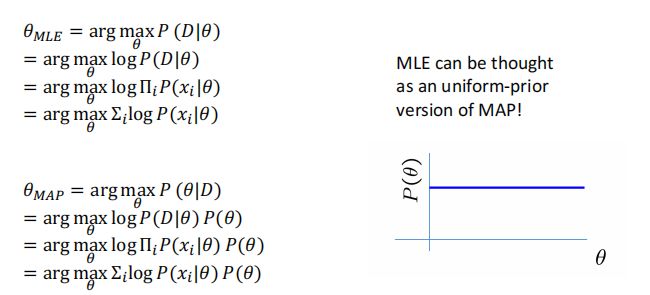
最大化后验概率,首先后验概率 = 先验概率 * likehood
-
在MLE中,核心思想是最大化likehood,是不需要先验知识的,只需要输入观测数据.缺点:在给定样本不多的情况下,似然估计的参数不一定对
-
所以在MAP中,用最大后验概率,其实是综合了给定的样本和先验知识
可能会考当把先验知识 prior =1(均匀先验知识),则MLE和MAP等价
Non-parametric Classification
优点:可以用在任意分布,且不需要知道概率密度函数的形式
Density Estimation
其实就是用样本算直方图
Dimensionality Reduction(降维)
Lecture 5
Data Scaling
对数据进行预处理,归一化,防止部分features数值过大,不利于后续操作
Dimensionality Reduction
Greedy Forward Feature Selection:从空的features集合中不断加最好的特征
Greedy Backward Feature Selection:从所有的features集合中不断删除最坏的特征
PCA
一种数据降维的方法,
question
maxmize the variance from the new data
minimize reconstruction error
main idea
基于特征值分解协方差矩阵实现PCA算法
-
计算出协方差矩阵
-
利用特征分解方法求协方差矩阵的特征值与特征向量
-
取出特征值最大的k个特征向量组成新的空间
基于SVD分解协方差矩阵实现PCA算法
-
去平均值,即每一位特征减去各自的平均值。
-
计算协方差矩阵。
-
通过SVD计算协方差矩阵的特征值与特征向量。
-
对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
-
将数据转换到k个特征向量构建的新空间中。
Eigenfaces
Lecture 6
Fisher's Linear Discriminant Analysis
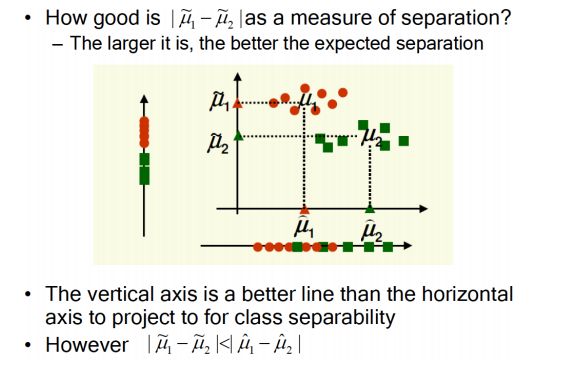
把分类集合投影到一条线上进行分类
question:
explain why maximizing the distance between the projected class means is not sufficient for separating?
不能简单的用一个维度的均值去分类
maybe have many overlapping parts,such like:
main idea
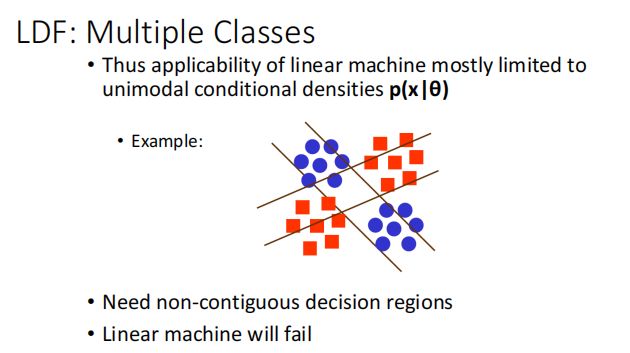
LDF:Linear Discriminant Functions
与Fisher 不同,Fisher 是投影到一条线上进行分类,LDF是根据在线的哪一边进行分类.
可能会考!
LDF 对于 不连续的决策区域无法正常工作
Lecture 7
Linear Regression
步骤:
-
Assume a linear model: Y = β0 + β1 X
-
Find the line which “best” fits the data, i.e. estimate parameters β0 and β1(训练:用最小误差进行拟合)
-
Check assumptions of model(验证)
-
Draw inferences and make predictions(测试)
Five Assumptions of Linear Regression
-
Existence: for each fixed value of X, Y is a random variable with finite mean and variance (对于每一个给定的X,Y都是随机的但是有一个有限的均值和方差)
-
Independence: the set of Yi are independent random variables given Xi(对于给定Xi,Yi是独立的随机变量,和X没有关系)
-
Linearity: the mean value of Y is a linear function of X(Y的均值对于x是一个线性的函数)
-
Homoscedasticity: the variance of Y is the same for any X(对于任意X,Y是同方差的)
-
Normality: For each fixed value of X, Y has a normal distribution (by assumption 4, σ2 does not depend on X)(对于任意X,Y是一个正态分布)
Estimating β0 and β1
实际上就是拟合 预测值和标签值的差 的平方和 最小。(MSE最小均方误差法----Lec8)
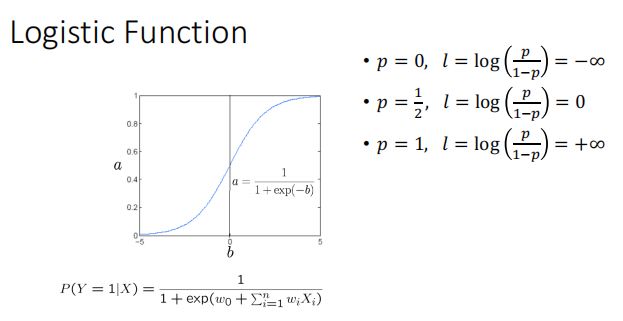
Logistic Regression
Aim: to learn Learn P(Y|X) directly by using the way like Linear Regression
实质:利用 l = a+bx 做线性回归,然后讲 l 带入 logistic function表示概率p
损失计算:
利用极大似然函数法,拟合逻辑回归中的参数(a,b)
逻辑回归模型的数学形式确定后,剩下就是如何去求解模型中的参数。在统计学中,常常使用极大似然估计法来求解,即找到一组参数,使得在这组参数下,我们的数据的似然度(概率)最大。
设:
似然函数:
为了更方便求解,我们对等式两边同取对数,写成对数似然函数:
在机器学习中我们有损失函数的概念,其衡量的是模型预测错误的程度。如果取整个数据集上的平均对数似然损失,我们可以得到:
即在逻辑回归模型中,我们最大化似然函数和最小化损失函数实际上是等价的。
逻辑回归的损失函数是:(计算方法可以用后面讲到的梯度下降)
Linear Discriminant Functions(线性判别方程)
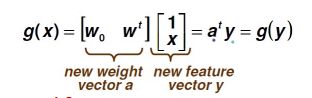
Augmented Feature Vector:
相当于多添加了一维的数据
判别形式:
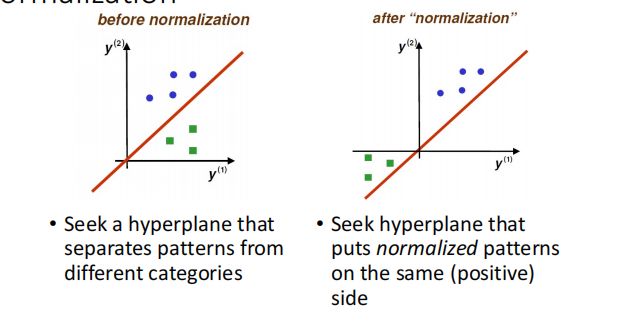
Normalization:
将第二类的输入变成原输入的反数,这样做是为了,简化方法,只要满足
就是分类正确的.
Solution Region
两种求解方法
Optimization:
将目标函数进行求导,算导数等于0的时候,缺点:解方程复杂,且对于现在的一些问题(深度学习),不太可能写出求导方程。
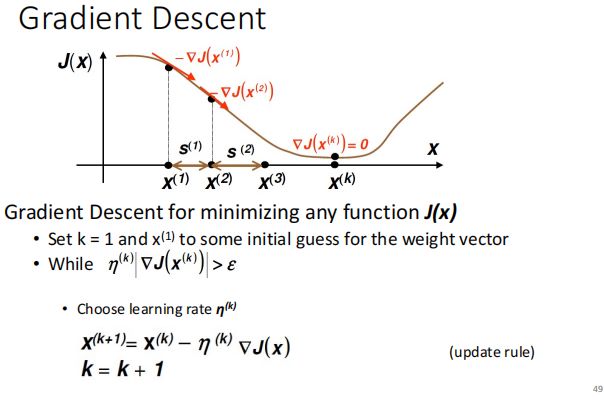
Gradient Descent(梯度下降)
更新weight vector方法:利用前一次的算出来的目标函数的导数,与目前的weight vector进行想减。
理解:梯度可以表示为目标函数下降的方向,我们只需要不断控制weight vector往这个方向前进,如下图。
优点:现在用的非常广泛,并且适合任意的目标函数
LDF Criterion Function
LDF最初设立的目标函数为错误样本的数量和,但是这是一个常数没有办法进行梯度下降,也没有办法进行求导为0,因此提出了后面的perceptron方法和MSE方法(与LDF最初设定方法主要不同就在于目标函数的设定)
注意:LDF 包含 Perceptron 和 MSE
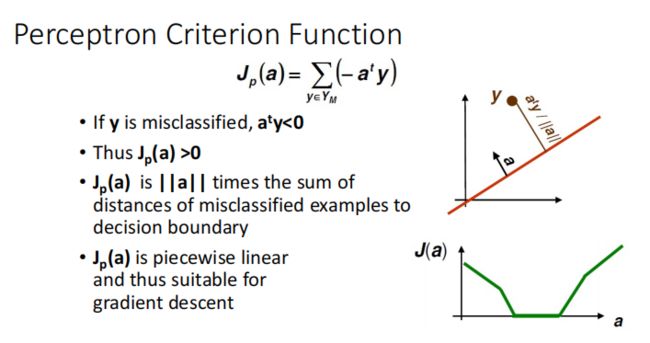
Perceptron(感知机)
感知器得目标函数为所有分错样本的距离和,目的就是最小化这个目标函数。
利用梯度更新方法:
因为目标函数对于y求导之后只剩下y了,所以梯度与a没有关系
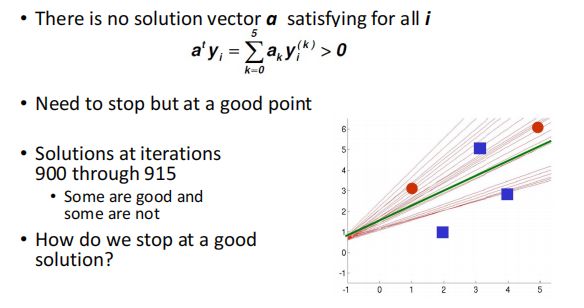
Non-separable Example && Convergence of Perceptron Rules
对于以上这种没有办法找到一个合适的分类线的情况,对于基础感知器或者线性判别分类器,它会一直继续分类,没有办法收敛。
此时我们可以设置合适的学习率
,相当于更新次数越多,梯度会越来越不想更新。
Lecture 8
Minimum Squared-Error Procedures
MSE 只是一种设立目标函数(损失)的一个方程而已。
MSE:求解方法:
-
利用求导为0(Optimization)
-
梯度下降Gradient Descent
Support Vector Machines
Support Vector Machines
LDF出现的问题:我们只是很好的拟合了训练集,当出现一个新的样本(十分接近我们的决策平面),我们就很容易将它分错。
因此就需要SVM(• Idea: maximize distance to the closest example)使最接近决策平面的两个点之间的距离最大。
公式:
(不考数学推理:)
求解||w||,需要利用拉格朗日函数,将原来的形式转变成:
如果利用核函数:
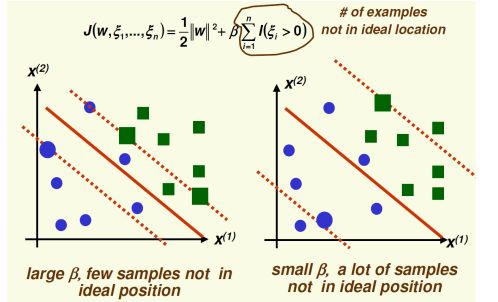
SVM: Non-Separable Case
通过设置 b 的大小来松弛间隔(允许多少点可以在这个间隔内)
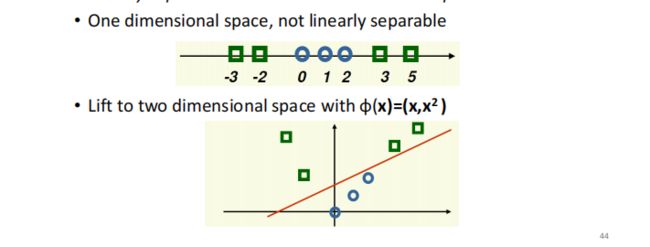
Nonlinear Mapping
利用转换方程实现非线性映射:
Kernels(SVM的核函数)
因为许多样本并不是线性可分的(用一条线就能够分出来),因此需要用到核函数(改变决策平面的形状)
核函数一定是半正定的
核函数类型(了解):
Nonlinear SVM Step-by-Step
与之前步骤是一样的,只是改变了核函数(感兴趣可以看数学推导里面)
Multi-class SVMs
有两种考虑角度:One-against-all:一次性分出多类 Pairwise:多次两两分类
(1)One-Against-All
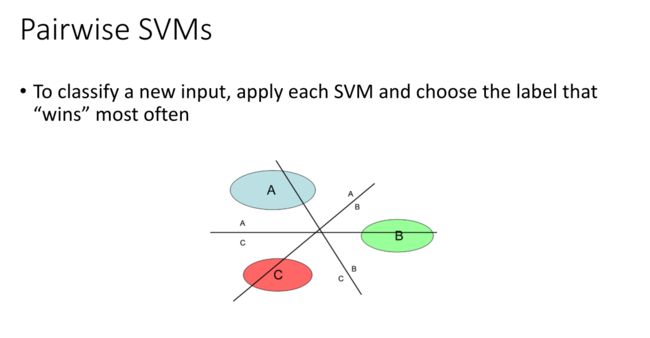
(2)Pairwise SVMs
实质:经过多次的两两分类 训练出 n*(n-1)/2 个支持向量机
SVM实现多分类的三种方案 - ZH奶酪 - 博客园 参考阅读~ thank 徐文熙 诸葛杨阳 for sharing
Lecture 9
Ensemble Classifiers (集成分类器)
利用多个分类器集成来提高分类效果
主要分为 Bagging 和 boosting,其中random forest 属于 bagging(感觉会考)
Bagging:
类似于投票机制:随机选取样本,利用每一次随机选取的训练集训练一个分类器,最后通过所有分类器进行投票来获得最后的分类效果。
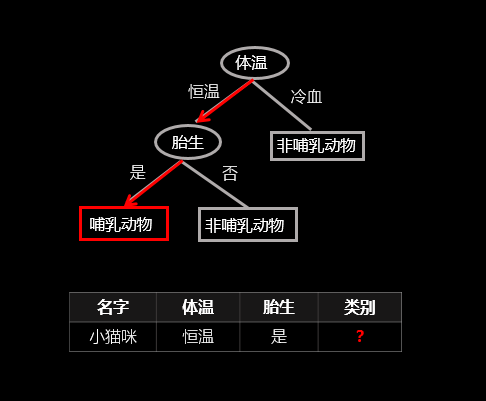
Decision Tree(决策树)
是一个树状的分类器,每一个节点的选择是根据信息增益熵选择的
感兴趣可以看:(考试应该不考)
决策树(decision tree)(一)——构造决策树方法_天泽28的专栏-CSDN博客_决策树
Random Forest:(随机森林)
就是把决策树当成弱分类器,然后利用Bagging方法,投票决定最后的分类。
Advantages of Random Forests
-
Very high accuracy – not easily surpassed by other algorithms
-
Efficient on large datasets
-
Can handle thousands of input variables without variable deletion
-
Effective method for estimating missing data, also maintains accuracy when a large proportion of the data are missing
-
Robust to label noise
-
Can be used in clustering, locating outliers and semi-supervised learning
Boosting
与bagging不同点在于,不是随机的选择每一次的训练样本(有规则的)
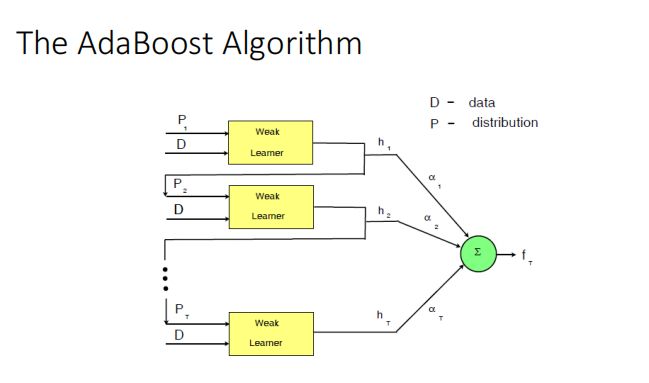
以AdaBoost为例:
-
第一次均匀的选取样本
-
之后会根据上一次选取的样本的错误率来更新,错误率越大就增加选取概率(为的是能够更好地训练分不对的点)
-
最后地分类由每一个分类器以及该分类器地错误率联合决定(sign是一个激活函数)
Random Forests vs. Boosting
Lecture 10
Unsupervised Learning(Clustering)
为什么要用非监督学习:
Distance Measures:
考虑问题:
-
Fix the number of clusters to k(分成几类)
-
Find the best clustering according to the criterion function (number of clusters may vary)(怎么分)
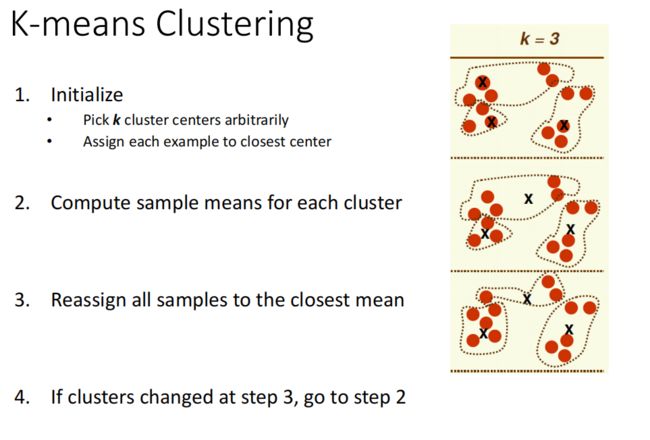
K-means Clustering
一种迭代地算法 Iterative optimization algorithms
-
人为选取要分地类数,上图k=3,并且随机初始化三个中心点,自动分类,距离哪个中心点近就是哪一类
-
计算每一个聚类地mean(均值)
-
重新将所有的点依据第二步的均值分类。
-
重复2 3 步骤 直到所有点不变
第二步的均值经常用距离(Distance Measures)来计算
Hierarchical Clustering(层次聚类)
由来:K-means 聚类举要实现确定K值和初始聚类中心点的选择,对于一部分数据不是很实用,因此提出了层次聚类。
主要分为以下两种算法:
1.Agglomerative (bottom up) procedures:(凝聚法)
1.将样本集中的所有的样本点都当做一个独立的类簇;
repeat:
-----------------------------------------------------------------------
2.计算两两类簇之间的距离(后边会做介绍),找到距离最小的两个类簇c1和c2;
3.合并类簇c1和c2为一个类簇;
-----------------------------------------------------------------------
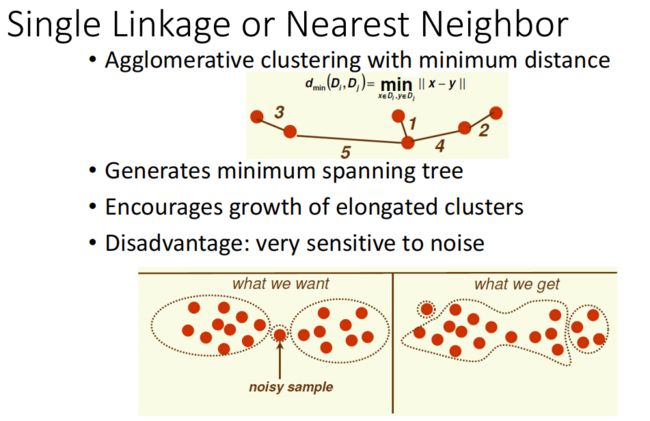
直到: 达到聚类的数目或者达到设定的条件1.1.Agglomerative clustering with minimum distance(用最小距离作为簇间的距离)
有利于细长数据的分类,对噪声很敏感
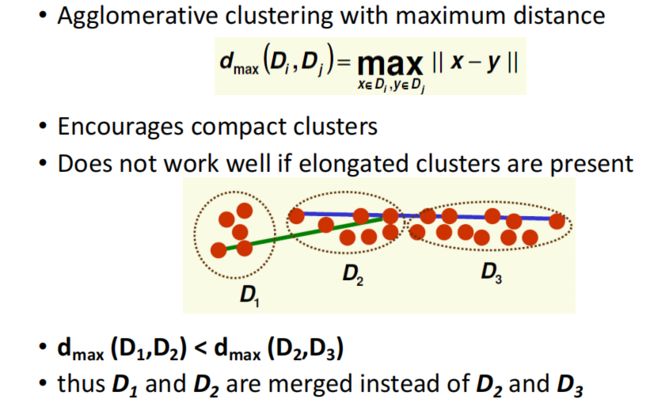
1.2.Agglomerative clustering with maximum distance(用最大的距离作为簇间距离)
对于紧凑形的数据能够很好的作用,对于细长的数据不能很好的工作
1.3Average and Mean Agglomerative Clustering:
mean聚类比avg更加节省,应该值得是在程序中可以用矩阵运算吧,不用遍历每个点(猜的)
2.Divisive (top down) procedures:(分裂法)
分裂法指的是初始时将所有的样本归为一个类簇,然后依据某种准则进行逐渐的分裂,直到达到某种条件或者达到设定的分类数目。用算法描述: 输入:样本集合D,聚类数目或者某个条件(一般是样本距离的阈值,这样就可不设置聚类数目) 输出:聚类结果 1.将样本集中的所有的样本归为一个类簇;
分裂法指的是初始时将所有的样本归为一个类簇,然后依据某种准则进行逐渐的分裂,
直到达到某种条件或者达到设定的分类数目。用算法描述:
输入:样本集合D,聚类数目或者某个条件(一般是样本距离的阈值,这样就可不设置聚类数目)
输出:聚类结果
1.将样本集中的所有的样本归为一个类簇;
repeat:
--------------------------------------------------------------------------------
2.在同一个类簇(计为c)中计算两两样本之间的距离,找出距离最远的两个样本a,b;
3.将样本a,b分配到不同的类簇c1和c2中;
4.计算原类簇(c)中剩余的其他样本点和a,b的距离,若是dis(a)两个簇之间的距离计算:
凝聚法和分裂法比较
(1)凝聚法通常更快
(2)分裂法不会因为局部数据而误判(因为分裂法是自上到下的,是从全局出发的,所以不会被局部数据误判)
Clustering Summary
-
能够发现数据的结构特性
-
能够应用在不同的领域
-
聚类对于人类来说比较简单,对于电脑来说比较复杂(人眼一下就能看出来,电脑需要迭代聚类)
-
应用聚类算法很简单,但是如何去评估它的表现很难
-
没有通用的聚类算法,都需要根据数据去调整聚类算法
Expectation Maximization
参考:如何通俗理解EM算法_结构之法 算法之道-CSDN博客_em算法
引子:
-
我们已经学习过对于非监督学习(不给标签),我们有Nonparametric approach(clustering)方法
-
对于模型参数估计我们有parametric approach(MLE)方法
其中Nonparametric approach(clustering)中不需要计算参数(概率分布)
而parametric approach(MLE)我们需要知道分类情况
但是在真正的Unsupervised Learning情况下,我们是不知道分类标签,但如果需要去计算它的概率分布就不太容易进行.
举个例子:
例子1. 假定我们需要统计七月在线10万学员中男生女生的身高分布,怎么统计呢?考虑到10万的数量巨大,所以不可能一个一个的去统计。对的,随机抽样,从10万学员中随机抽取100个男生,100个女生,然后依次统计他们各自的身高。
例子1我们可以用MLE来分别拟合男女生的正太分布模型
例子2: 比如这100个男生和100个女生混在一起了。我们拥有200个人的身高数据,却不知道这200个人每一个是男生还是女生,此时的男女性别就像一个隐变量。
对于例子2来说就要用到接下来的 Expectation Maximization
看这个问题其实有点像 chicken-and-egg problem,先有鸡还是先有蛋
我们想获得男女的正太分布模型,就得知道男女分类情况,想知道男女分类情况就得知道男女的条件概率 P(性别|身高),这两者不能同时实现
EM算法:(官方定义)
最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。 最大期望算法经过两个步骤交替进行计算, 第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值; 第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
通俗理解
我们拿例子2为例:隐藏变量为性别 1.我们先初始化男女正态分布的参数(乱设都可以) 2.利用第一步的正态分布,获得男女的条件概率,对已知的数据进行男女分类 3.利用第二步得到的男女分类,重新计算正太分布的参数值(MLE) 重复2 3 步直到收敛
其中 官方定义中:
第一步计算期望值得是根据模型参数来计算出隐形变量的后验概率(其实就是隐形变量的期望)
第二部最大化,指的就是利用第一步得到的隐形变量来计算下一步的模型参数
EM Summary
-
如果选定的概率模型不对,结果不会好
-
如果隐变量的个数选的有问题,结果也会不好
(据说不考)Lecture 11
神经网络基础知识
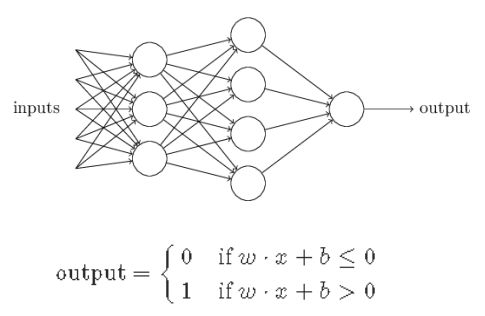
Perceptrons感知机
可以把他看成神经网络的组成基础,想人脑的细胞一样
output =激活函数(w*x+b)
其中w是神经元自有的参数矩阵,是可以通过反向传播学习的,b为偏执
激活函数包括
-
max()函数
-
Sigmoid()将概率拟合在[0,1]
-
Relu:作用 映射是局部线性的
为什么要用激活函数(可能会考)
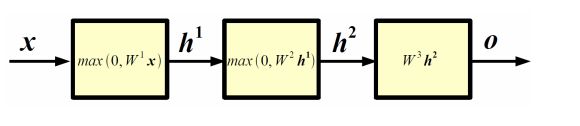
激活函数使得网络从线性变成非线性,如果没有激活函数,多层网络就没有意义,多层网络会变成一层网络.
以这个例子,没有激活函数max相当于一层网络 输出x*nwe(W)
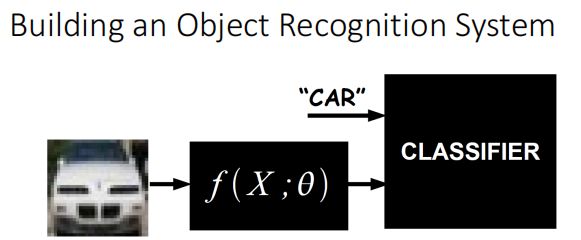
工作流程(概念)
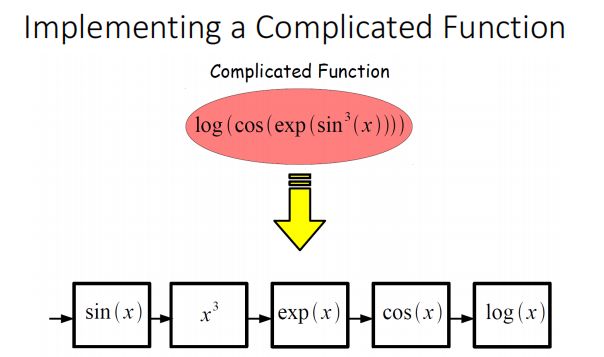
以汽车识别为例子,我们需要一个复杂的函数来判断是否为汽车
可以用多层网络来实现
神经网络实现流程
-
利用训练集输入网络
-
设计我们的目标函数,目标函数:在图像分类中就是要最小化分类错误
-
通过目标函数,计算loss
-
通过反向传播(链式法则Chain rule)
-
利用optimization算法更新网络参数(每个感知机中的参数):
Some question
最后一个问题解释:为什么需要很多层?
因为每一层的都可以重复使用,我们知道神经网络的每一层是用来提取特征的.对于不同的类别,有些特征是相同的,比如摩托和汽车都有轮胎,所以提取摩托特征的网络层是可以重复使用的.
-----------------------------------------------------------------------------------------感谢贾神、陈工友,无私奉献