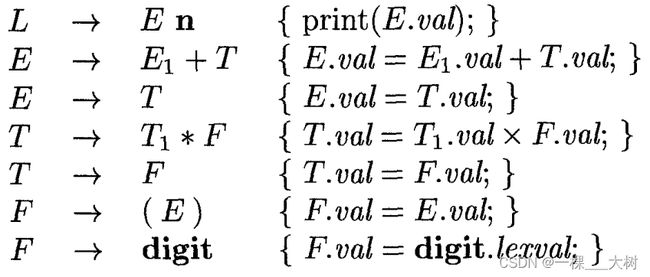【编译原理】6—语法制导翻译Syntax-Directed Translation(SDD、SDT详细介绍)
6 语法制导翻译Syntax-Directed Translation
⭐⭐⭐⭐⭐⭐
Github主页https://github.com/A-BigTree
项目链接https://github.com/A-BigTree/college_assignment
⭐⭐⭐⭐⭐⭐
文章目录
- 6 语法制导翻译Syntax-Directed Translation
-
- 6.1 语法制导定义SDD
-
- 6.1.1 属性分类
- 6.1.2 在语法分析树的结点上对SSD求值⭐
- 6.2 SDD的求值顺序
-
- 6.2.1 依赖图
- 6.2.2 属性求值的顺序
- 6.2.3 S属性的定义⭐
- 6.2.4 L属性的定义⭐
- 6.2.5 具有受控副作用的语义规则
- 6.3 语法制导的应用
-
- 6.3.1 抽象语法树的构造
- 6.3.2 类型结构
- 6.4 语法制导的翻译方案
-
- 6.4.1 后缀翻译方案
- 6.4.2 产生式内部带有语义动作的SDT
- 6.4.3 从SDT中消除左递归
- 6.4.4 L属性定义的SDT
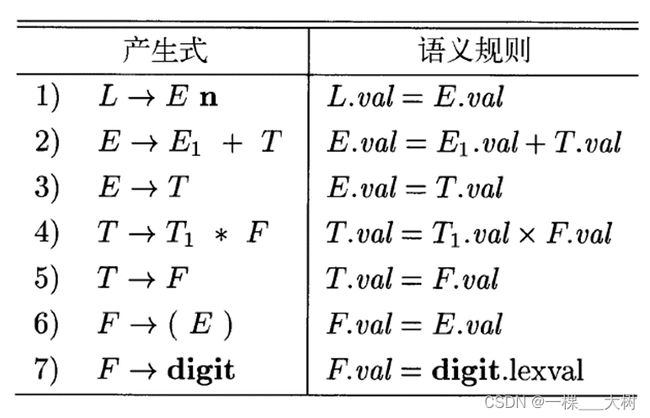
6.1 语法制导定义SDD
语法制导定义(Syntax-Directed Definition,SDD)是一个上文文无关文法和 属性及规则 的结合。
属性和文法符号相关联,而规则和产生式相关联。如果X是一个符号而a是X的一个属性,那么我们用X.a来表示a在某个标号为X的分析树结点上的值。属性可以有很多种类型,比如数字、类型、表格引用或串。
6.1.1 属性分类
- 综合属性(synthesized attribute):自下而上传递信息。在分析树节点N上的非终结符号A的综合属性是由N上的产生式所关联的语义规则来定义。
- 继承属性(inherited attribute):自上而下传递消息。在分析树节点N上的非终结符号B的继承属性是由N的父节点上的产生式所关联的语义规则来定义。
终结符只有综合属性,它由语法分析器提供。非终结符既可以有综合属性也可以有继承属性,但文法开始符号的继承属性作为属性计算前的初始值。
- 一个只 包含综合属性 的SDD称为S属性(S-attribute)的SDD;
- 一个S属性的SDD可以和一个LR语法分析器一起自然地实现;
- 一个没有副作用的SDD有时也称为属性文法(attribute grammar);一个属性文法的规则仅仅通过其他属性值和常量值来定义一个属性值;
6.1.2 在语法分析树的结点上对SSD求值⭐
一个显示了它的各个属性的值的语法分析树称为 注释语法分析树(annotated parse tree)。
我们对一棵语法分析树的某个结点的一个属性进行求值之前,必须首先求出这个属性值依赖的所有属性值。
- 对于综合属性,我们可以按照任何自底向上的顺序计算它们的值,比如对语法分析树进行后序遍历的顺序;
- 对于同时具有继承属性和综合属性的SSD,不能保证有一个顺序来对各节点上的属性进行求值;
- 从计算角度看,给定一个SDD,很难确定是否存在某棵语法分析树使得SDD属性值之间具有依赖关系。幸运的是,存在一个SDD的有用子类,它们能够保证对每棵语法分析树都存在一个求值顺序,后面将进一步讨论;
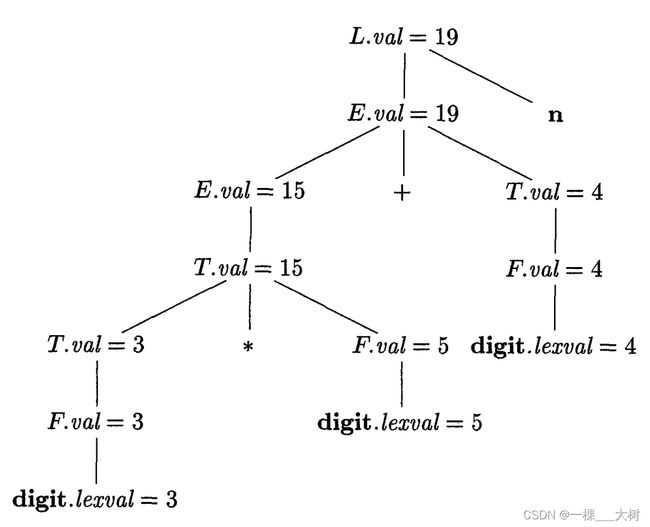
示例1:
写出 3 ∗ 5 + 4 n 3*5+4n 3∗5+4n的注释语法分析树。
自下而上
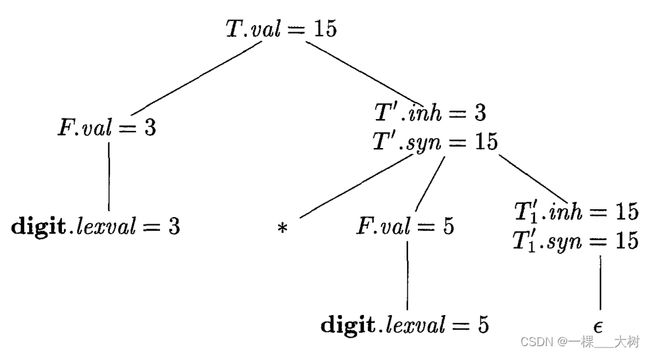
示例2:
对于如下文法:
写出 3 ∗ 5 3*5 3∗5的注释文法分析树。
自顶向下
6.2 SDD的求值顺序
6.2.1 依赖图
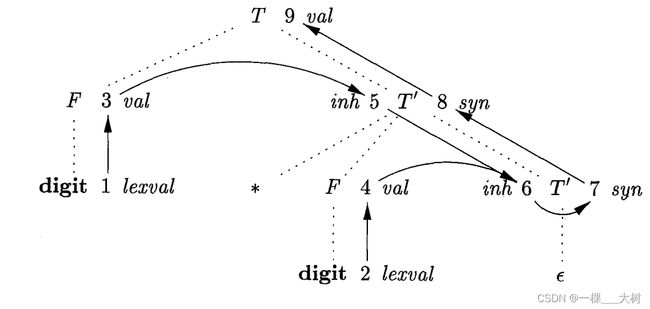
依赖图(dependency graph) 可以确定一棵给定的语法分析树中各个属性实例的求值顺序。注释语法分析树显示了各个属性的值,而依赖图可以帮助我们确定如何计算这些值。
依赖图描述了某个语法分析树中的属性实例之间的信息流。从一个属性实例到另一个实例的边表示计算第二个属性实例时需要第一个属性实例的值。图中的边表示语义规则所蕴含的约束。
实例2依赖图如下:
6.2.2 属性求值的顺序
如果依赖图中有一条从结点M到结点N的边,那么要先对M对应属性求值,再对N对应的属性求值。因此,所有的可行求值顺序就是满足下列条件的结点顺序 N 1 , N 2 , … , N k N_1,N_2,\dots,N_k N1,N2,…,Nk:如果有一条从结点 N i N_i Ni到 N j N_j Nj的依赖图的边,那么 i < j i
如果图中存在任意一个环,那么就不存在拓扑排序。也就是说,没有办法在这棵语法分析树上对相应的SDD求值。然而,如果图中没有环,那么总是至少存在一个拓扑排序。
6.2.3 S属性的定义⭐
第一种SDD类型的定义如下:
- 如果一个SDD的每个属性 都是综合属性,它就是S属性的(S-attribute)。
S属性的定义可以在自底向上语法分析的过程中实现,因为一个自底向上的语法分析过程对应一次后序遍历。
6.2.4 L属性的定义⭐
第二种SDD称为L属性定义(L-attributed definition)。这类SDD的思想是在一个产生式体所关联的各个属性之间,依赖图的边总是从左到右,而不能从右到左。每个属性必须是:
- 综合属性;
- 继承属性,但是它的规则具有如下限制。假设存在一个产生式 A → X 1 X 2 … X n A\rightarrow X_1X_2\dots X_n A→X1X2…Xn,并且有一个通过这个产生式所关联的规则计算得到的继承属性 X i . a X_i.a Xi.a。那么这个规则只能使用:
- 和产生式头A关联的继承属性;
- 位于 X i X_i Xi左边文法的文法符号实例 X 1 , X 2 , … , X i − 1 X_1,X_2,\dots,X_{i-1} X1,X2,…,Xi−1相关的继承属性或者综合属性;
- 和这个 X i X_i Xi的实例本身相关的继承属性或综合属性,但是在由这个 X i X_i Xi的全部属性组成的依赖图中不存在环;
结点使用信息“来自上边或左边”,要么是综合属性。
6.2.5 具有受控副作用的语义规则
对于SDD,我们在属性文法和翻译方案之间找到一个平衡点。属性文法没有副作用,并支持任何与依赖图一致的求值顺序。翻译方案要求按从左到右的顺序求值。
控制SDD中的副作用:
- 支持那些不会对属性求值产生约束的附带副作用;
- 对允许的求值顺序添加约束,使得以任何允许的顺序求值都会产生相同的翻译结果;
6.3 语法制导的应用
6.3.1 抽象语法树的构造
我们将使用具有适当数量的字段的对象来实现一棵语法树的各个结点。每个对象将有一个op字段,也就是这个结点的标号。这些对象将具有如下所述的字段:
- 如果结点是一个叶子,那么对象将有一个附加的域来存放这个这个叶子结点的词法值。构造函数 L e a f ( o p , v a l ) Leaf(op,val) Leaf(op,val)创建一个叶子对象。我们也可以把结点看作记录,那么 L e a f Leaf Leaf就会返回一个指向与叶子节点对应的新纪录的指针;
- 如果结点是内部结点,那么它的附加字段的个数和结点在语法树中的子节点个数相同。构造函数的 N o d e Node Node带有两个或多个参数: N o d e ( o p , c 1 , c 2 , … , c k ) Node(op,c_1,c_2,\dots,c_k) Node(op,c1,c2,…,ck),该函数创建一个对象,第一个字段的值为op,其余k个字段的值为 c 1 , … , c k c_1,\dots,c_k c1,…,ck;
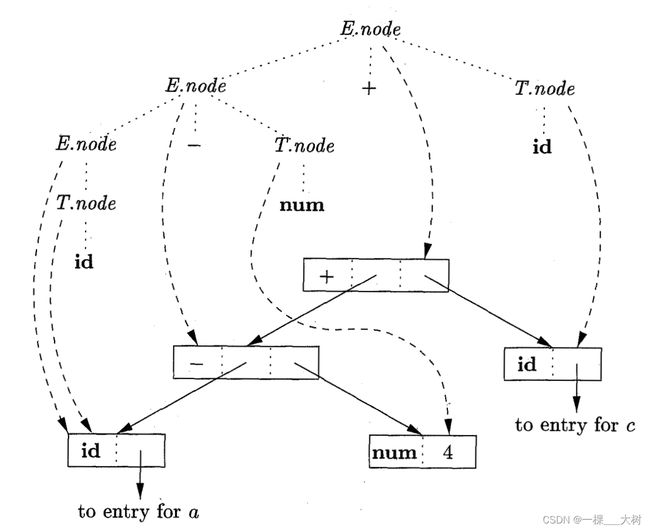
下面为S属性定义为一个简单的表达式文法构造出语法树:
下面为 a − 4 + c a-4+c a−4+c的抽象语法树:
6.3.2 类型结构
当语法分析树的结构和输入的抽象语法树的结构不同时,继承属性是很有用的。在这种情况下,继承属性可以用来将信息从语法分析树的 一部分传递到另一部分。
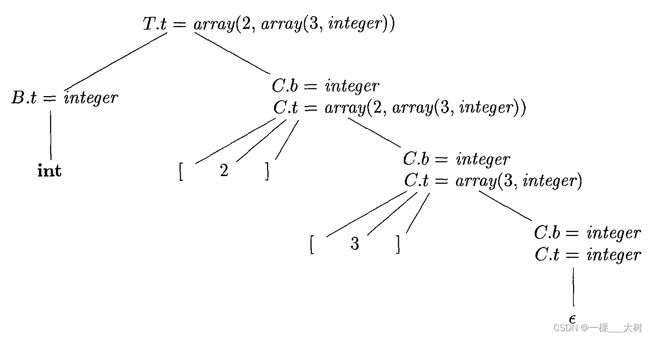
下图为数组类型的语法制导的翻译:
输入串 i n t [ 2 ] [ 3 ] int[2][3] int[2][3]翻译如下图:
6.4 语法制导的翻译方案
语法制导的翻译方案(syntax-directed translation scheme,SDT)是在其产生式体中嵌入了程序片段的一个上下文无关文法。这些程序片段称为 语义动作,它们可以出现在产生式体中的任何地方。
任何SDT都可以通过下面的方法实现:首先建立一棵语法分析树,然后按照从左到右的深度优先顺序来执行这些动作,也就是说在一个前序遍历过程中执行。我们主要关注如何使用SDT来实现两类重要的SDD:
- 基本文法可以用LR技术分析,且SDD为S属性;
- 基本文法可以用LL技术分析,且SDD为L属性;
可以在语法分析过程中实现的SDT可以按照如下的方式识别:将每个内嵌的语义动作替换成一个独有的标记非终结符号(marker nonterminal)。每个标记非终结符M只有一个产生式 M → ε M\rightarrow \varepsilon M→ε。如果带有标记非终结符号的文法可以使用某个方法进行语法分析,那么这个SDT就可以在语法分析过程中实现。
6.4.1 后缀翻译方案
至今为止,最简单的实现SDD的情况是文法可以用自底向上方法来分析且该SDD是S属性定义。在这种情况下,我们可以构造出一个SDT,其中的每个动作都放在产生式的最后,并且在按照这个产生式将产生式体归约为产生式头的时候执行这个动作。所有动作都在产生式最右端的SDT称为后缀翻译方案。
下图为桌上计算器的后缀SDT:
6.4.2 产生式内部带有语义动作的SDT
动作可以放置在产生式体中的任何位置上。当一个动作左边的所有符号都被处理过后,该动作立刻执行。因此,如果我们有一个产生式 B → X { a } Y B\rightarrow X\{a\}Y B→X{a}Y,那么当我们识别到X(如果X是终结符号)或者所有从X推导出的终结符号(如果X是非终结符号)之后,动作a就会只自行。
- 如果语法分析过程是自底向上的,那么我们在X的此次出现位于语法分析栈的栈顶时,我们立刻执行动作a;
- 如果语法分析过程是自顶向下的,那么我们在试图展开Y的本次出现(如果Y是非终结符号)或者在输入中检测Y(如果Y是非终结符号)之前执行语义动作a;
6.4.3 从SDT中消除左递归
核心方法:在转换文法的时候,将动作当作终结符号处理。
实例:
E → E 1 + T { p r i n t ( ′ + ′ ) ; } ∣ T E\rightarrow E_1+T\{print('+');\}|T E→E1+T{print(′+′);}∣T
引用R表示E的余部,消除左递归后为:
E → T R R → + T { p r i n t ( ′ + ′ ) } R ∣ ε \begin{aligned} &E\rightarrow TR\\ &R\rightarrow +T\{print('+')\}R|\varepsilon \end{aligned} E→TRR→+T{print(′+′)}R∣ε
6.4.4 L属性定义的SDT
将一个L属性的SDD转换为一个SDT的规则如下:
- 把计算某个非终结符号A的继承属性的动作插入到产生式体中紧靠在A的本次出现之前的位置上。如果A的多个继承属性以无环的方式相互依赖,就需要对这些属性的求值动作进行排序,以便先计算需要的属性;
- 将计算一个产生式头的综合属性的动作放置在这个产生式体的最右端;
⭐⭐⭐⭐⭐⭐
Github主页https://github.com/A-BigTree
项目链接https://github.com/A-BigTree/college_assignment
⭐⭐⭐⭐⭐⭐