Lift Splat Shoot Encoding Images from Arbitrary Camera Rigs by Implicitly Unprojecting to 3D 论文阅读笔记
Lift, Splat, Shoot: Encoding Images from Arbitrary Camera Rigs by Implicitly Unprojecting to 3D 论文阅读笔记
论文链接:https://arxiv.org/abs/2008.05711
代码链接:https://github.com/nv-tlabs/lift-splat-shoot
一、 Problem Statement
single-image到multi-view的范式:对于 n n n个相机的数据,通常是使用一个single-image的检测器对所有的输入图像分别做检测,然后再通过内外参的后处理,汇总到车体坐标系上。这样的范式有以下三个优点:
- Translation equivariance
- Permutation invariance
- Ego-frame isometry equivariance
然而,上述的范式也有缺点,即使用来自单个图像检测器的后处理检测阻止了从基于车体本身做的预测到输入图像的反向梯度(我认为并不是好的端到端检测)。
二、 Direction
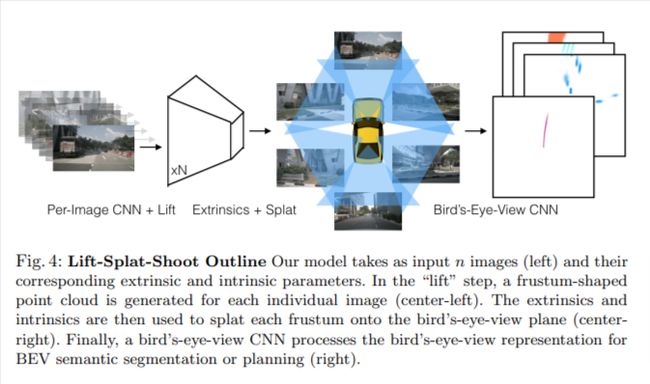
本文探索的是通过多路摄像头数据,直接在BEV下完成vehicle segmentation. drivable area, 和lane segmentation任务。提出 "Lift-Splat"模块,保证了上述三个优点的同时,也能够端到端的训练。也提出了一个Shooting模块(有关路径规划的,本文就不细讲了)。
- Lift: 这个操作就是通过生成一个视锥形的点云把图像升维到3D。
- Splat: 这个操作就是将所有视锥转换到一个参考平面。
- Shooting: 这个操作就是将预测出的路径转换到参考平面上,做一个端到端的路径规划。
三、 Method
给定了 n n n张图像, { X k ∈ R 3 × H × W } n \{X_k \in \R^{3 \times H \times W}\}_n {Xk∈R3×H×W}n,还有其对应的外参矩阵 E k ∈ R 3 × 4 E_k \in \R^{3 \times 4} Ek∈R3×4,内参矩阵 I k ∈ R 3 × 3 I_k \in \R^{3 \times 3} Ik∈R3×3, 寻找一个在BEV坐标系下的栅格化表征 y ∈ R C × X × Y y \in \R^{C \times X \times Y} y∈RC×X×Y。外参和内参矩阵共同定义了从参考坐标系 ( x , y , z ) (x,y,z) (x,y,z)到像素坐标系 ( h , w , d ) (h,w,d) (h,w,d)的映射。
1. Lift: Latent Depth Distribution
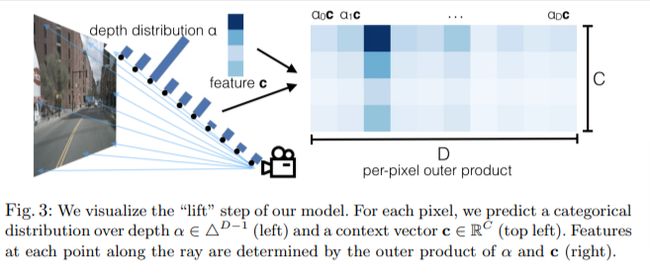
这一步的操作就是将2D图像转换到3D数据。但是2D到3D是缺少深度维度的,本文的做法是对每个像素生成一组深度。假如输入图像 X ∈ R 3 × H × W X \in \R^{3 \times H \times W} X∈R3×H×W,外参 E E E和内参 I I I, 用 p p p代表图像内的一个像素,作者用 d d d 代表这个像素的一组深度, { ( h , w , d ) ∈ R 3 ∣ d ∈ D } \{(h,w,d) \in \R^3 | d \in D \} {(h,w,d)∈R3∣d∈D},其中 h , w h, w h,w是像素坐标系, ∣ D ∣ |D| ∣D∣是一个深度集合。举个例子 { d 0 + Δ , . . . , d 0 + ∣ D ∣ Δ } \{d_0 +\Delta, ..., d_0 +|D| \Delta \} {d0+Δ,...,d0+∣D∣Δ}。这中间是没有可以学习的参数的。
通过上面方法,作者对每个像素建立了 D × W × H D \times W \times H D×W×H大小的点云。对于每个像素,网络会输出一个context vector c ∈ R C c \in \R^C c∈RC,和一个对于深度的分布 α ∈ Δ ∣ D ∣ − 1 \alpha \in \Delta^{|D|-1} α∈Δ∣D∣−1。特征 c d ∈ R C c_d \in \R^C cd∈RC是关于点 p d p_d pd的,定义如下:
c d = α d c c_d = \alpha_d c cd=αdc
若网络估计 α \alpha α为one-hot vector,则该方法与伪激光雷达方法相同;若网络估计深度均匀分布,则该方法与OFT。因此本文方法可以灵活地在两者范围内选择。
总之,作者是想对每个图片,生成一个函数 g c : ( x , y , z ) ∈ R 3 → c ∈ R C g_c:(x,y,z) \in \R^3 \rightarrow c\in \R^C gc:(x,y,z)∈R3→c∈RC。作者使用EfficientNet-B0对每个输入图片进行独立的处理。
2. Splat: Pillar Pooling
作者这一部分使用pointpillars框架,将"lift"部分输出的点云进行处理。"pillar"是一个无限高度的体素。将每个点赋值到其最近的Pillar,然后使用sum pooling来创建 C × H × W C \times H \times W C×H×W维度的Tensor。因此这个Tensor可以用CNN来进行BEV的推理。
对于BEV网络,作者使用了ResNet Blocks组合进行提取。
这里面有一些超参数,决定了模型的“分辨率”。
- 输入图像H x W。 本论文中,所有的实验输入图像大小为128x352,也相对于调整外参和内参。
- 另外一个就是BEV grid大小。x,y设置为-50到50,cell size为0.5x0.5m。所以就是200x200的体素大小。
- 预测D的范围,取4到45米。
总结
bev视角下做3D检测的工作,纯视觉的bev下检测一个难点就是深度信息的缺失,本篇论文中提供了可选的离散深度值,让2D像素寻找在3D世界中最合理的位置,取得了不错的效果。特征融合效果较好,实现端到端。