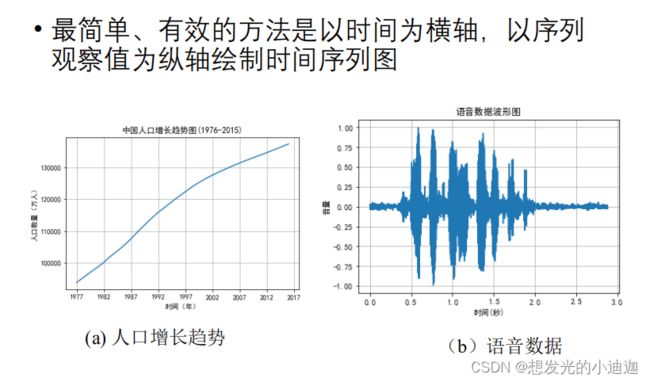
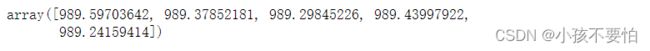时序数据和语音处理

时序数据

时序数据概述

• 即时间序列数据------用于时序预测
  作用：用来连续观察同一对象在不同时间点上获得的数据样本集
  处理目标：对给定的时间序列样本，找出统计特性和发展规律性，推测未来值
• 语音是一类特殊的时序数据
  识别语音对应的文本信息是当前人工智能的热点

观察时序数据

时序数据特性

• 循环性
  指时间序列的变动有规律地徘徊于趋势线上下并反复出现
• 季节性
  一年内随季节变换而发生的有规律的周期性变化，比如流感季，但更小单位的周期变动也被看成季节成分，如日交通流量反映了一天内“季节”变化情况
• 趋势性
  时间序列在长时间内所呈现出来的行为，指受某种根本性因素影响而产生的变动或缓慢的运动
• 波动
  围绕前3个要素随机性波动, 是一种无规律可循的变动。

时序数据特征的提取

提取方法有四种：

• 基于统计方法的提取（常利用df.describe()来获取一些常用特征值）
  提取数据波形的均值、方差、极值、波段、功率谱、过零率等统计特征，代替原时序数据作为特征向量。
• 基于模型的特征提取
  用模型去刻画时间序列数据，然后提取模型的系数作为特征向量
• 基于变换的特征提取
  通过变换使数据的特征突显出来，以便提取
  主要有时频变换和线性变换，如：快速傅里叶变换、小波变换和主成分分析
• 基于分形理论的特征提取
  分形是指具有无限精细、非常不规则、无穷自相似的结构
  在大自然中，海岸线、雪花、云雾这些不规则形体都属于分形，即部分与整体有相似性，可提取分维数作为特征参数。

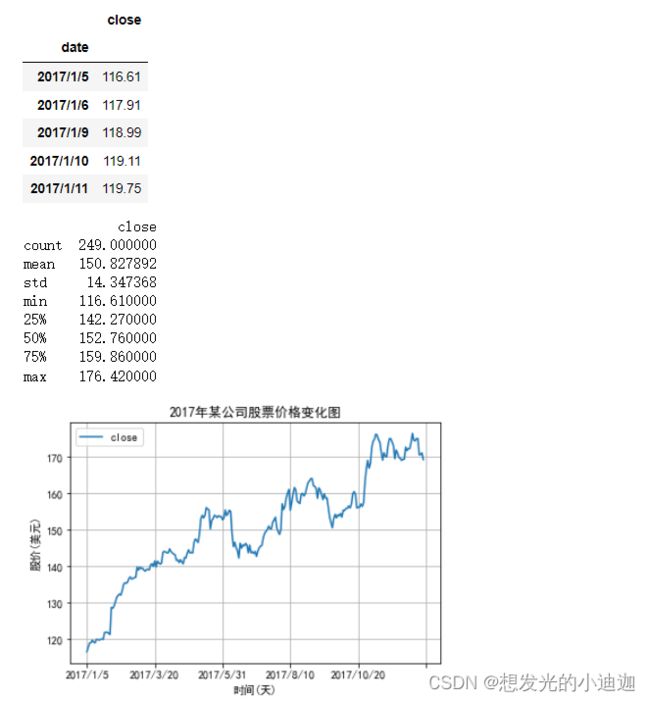
例题8-1：某公司2017年股票价格保存在数据集stockPrice.csv，绘制股票收盘价的时序图，并提取该时序数据的常用特征值。

数据特征说明
date:日期 open:开盘价 high:最高价 close:收盘价 volume:成交量 low:最低价

import pandas as pd
import matplotlib.pyplot as plt
'''设置中文字体，用来正常显示中文标签'''
plt.rcParams['font.sans-serif']= ['SimHei']
'''
usesols=[col1,col2,...]------从文件中只读取指定的列
index_col=0------设置第0列作为行索引
'''
df= pd.read_csv('E:\课\数据科学\data\stockPrice.csv', index_col= 0, usecols= [0,1])
display(df.head())
'''df.describe()------返回列表对应的基本统计量和分位数，此处用该函数是为了统计该序列的一些常用特征'''
print(df.describe())
'''
绘制时序图并添加图元
行索引自动为x轴刻度
'''
df.plot(title= '2017年某公司股票价格变化图', grid= True)
plt.xlabel('时间(天)')
plt.ylabel('股价(美元)')
plt.show()

运行结果显示为：

思考与练习1

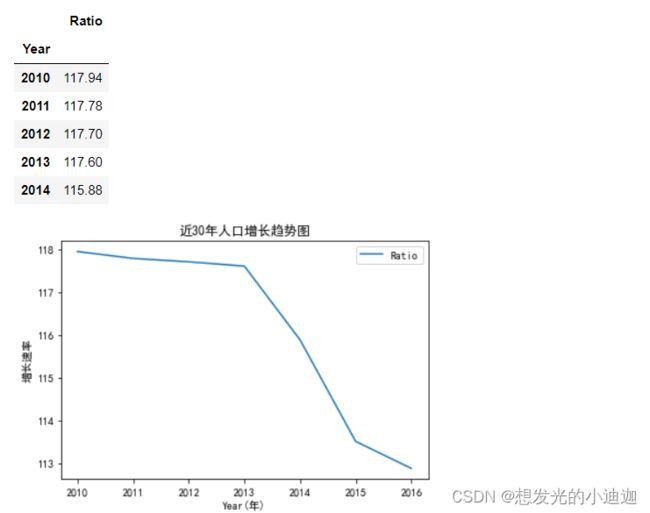
利用我国人口统计时序数据集（population.csv）绘制30年来我国人口增长的趋势图，如例题8-1所示。

import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']= ['SimHei']
df= pd.read_csv('E:\data\Population.csv',index_col= 0, usecols= [0,4])
display(df.head())
df.plot(title= '近30年人口增长趋势图')
plt.xlabel('Year(年)')
plt.ylabel('增长速率')
plt.show()

运行结果显示为：

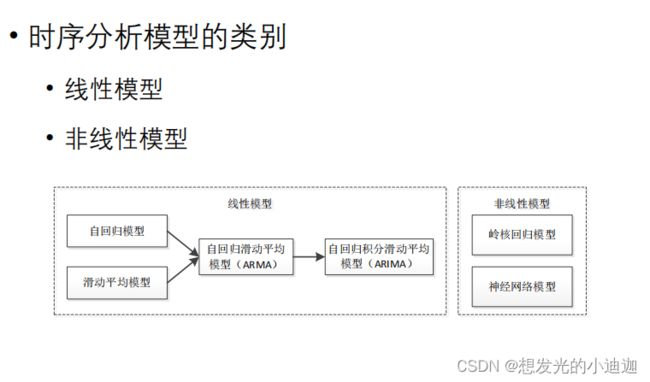
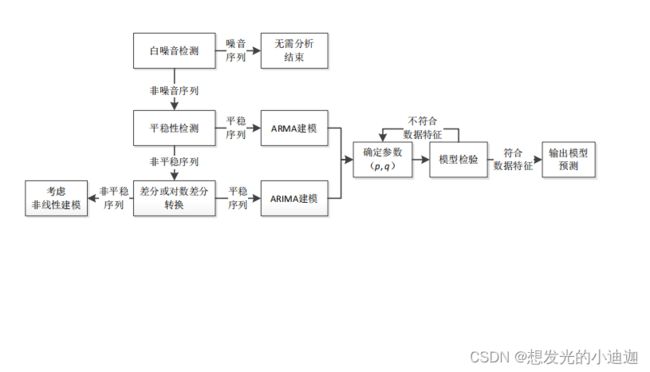
时序数据分析方法(模型类别)

线性模型

定义：用时间序列中前若干时刻的观察值的线性组合来描述以后某时刻的值。
线性时序模型首先考虑序列平稳性
线性时序模型分为：平稳时间序列和非平稳时间序列

• 平稳时间序列------采用自回归滑动平均模型(ARMA)处理
  即均值和方差均为常数的时间序列，其自协方差函数与起点无关
• 非平稳时间序列
  可考虑将其经过差分转化为平稳时间序列，然后在用自回归滑动平均模型(ARMA)处理。

线性模型的时序数据分析过程

• Step1：纯随机性检验------用于检测是否为白噪音
  使用Q(Pierce-Box)或LB(LJung-Box)统计量来进行白噪声检验
  from statsmodels.stats.diagnostic import acorr_ljungbox
  纯随机序列也被称为白噪声序列，特征为：

自相关系数为0
数据中没有可提取的信息，无需进一步分析
序列中各项之间没有任何相关关系，数据波动完全随机

• Step2：平稳性检验------用于检测是否为平稳序列
  采用单位根(ADF, Augment Dickey-Fuller)检验进行定量分析
  平稳序列特征：

具有短期相关性；
在时间序列图上，序列值将在一个常数附近随机波动；
没有明显的趋势性或周期性。

• Step3：ARIMA建模------用于将非平稳的时序转换为平稳序列，若本身为平稳序列则跳过该步。

通过n次差分运算将非平稳的时序转换为平稳序列，然后获取ARIMA(n,p,q)模型的参数p和q

• Step4：ARMA建模、定阶------主要是为了获取参数
  计算平稳时间序列的自相关函数和偏相关函数通过对自相关图和偏自相关图的分析获得参数p和q的大概范围。
  根据AIC信息准则，计算候选参数空间内每个模型的AIC值，最小的AIC值对应的p和q为最佳的阶数，此过程为定阶。
• Step5：预测
  使用ARIMA或ARMA模型对时间序列进行预测，计算预测值的误差与置信区间，观察有效预测周期。

判断是否为白噪声、平稳性序列方法

当LB白噪声检验结果的p值小于0.05时，则不是白噪声
当单位根(ADF)平稳性检验结果的p值小于0.05时，则是平稳性序列

相关重要代码如下：

• 设置中文字体
  plt.rcParams['font.sans-serif']= ['SimHei']
• 正负号正常显示
  plt.rcParams['axes.unicode_minus']= False
• 画自相关图
  from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data)
• 利用LB统计量进行某一列白噪声检验
  from statsmodels.stats.diagnostic import acorr_ljungbox as LB
print('LB白噪声检验结果为：',LB(data['股价'], lags= 1))
  利用单位根(ADF)进行某一列平稳性检验
  from statsmodels.tsa.stattools import adfuller as ADF
print('ADF-平稳性检验结果：', ADF(data0['股价']))
• n次差分并删除非法值
  D_data= data.diff().dropna()
D_data.columns= ['股价差分']
• 差分后的时序图
  D_data.plot()
• 偏自相关图
  from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data, method= 'ywm')
• ARIMA模型初始化
  from statsmodels.tsa.arima.model import ARIMA
arima= ARIMA(data, order=(p, 1, q)).fit()
  模型预测报告：arima.summary()
  对未来n天进行预测：arima.forecast(n)

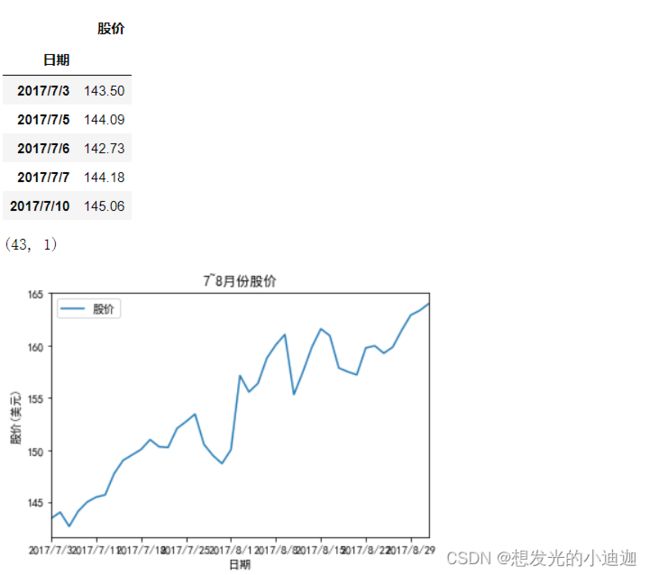
例题8-2：从例8-1股票数据中选取7～8月份股票收盘价，保存到stockClose.csv文件。采用线性方法建模分析数据，预测股价，并与实际股价进行比较。

'''Step1：数据处理并显示数据的折线图'''
import pandas as pd
import matplotlib.pyplot as plt
'''设置中文字体，使中文能够正常显示'''
plt.rcParams['font.sans-serif']= ['SimHei']
'''正常显示正负号'''
plt.rcParams['axes.unicode_minus']= False
data= pd.read_csv('E:\data\stockClose.csv', index_col= '日期', encoding= 'ANSI')
display(data.head())
display(data.shape)
'''xlim=[0,42]代表x轴刻度从0到42共有43个刻度'''
data.plot(title= '7~8月份股价', xlim= [0,42])
plt.xlabel('日期')
plt.ylabel('股价(美元)')
plt.show()

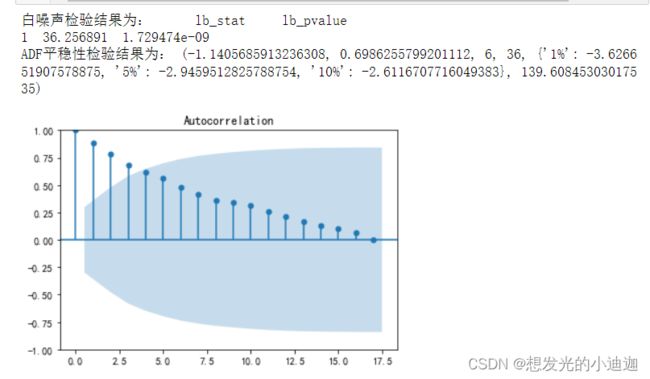
'''Step2：纯随机性和平稳性检验并画出股票数据的自相关图并输出纯随机性LB检验和ADF检验的结果'''
'''画自相关图'''

from statsmodels.graphics.tsaplots import plot_acf 
plot_acf(data)

'''利用LB统计量进行白噪音检验'''
from statsmodels.stats.diagnostic import acorr_ljungbox as LB
print("白噪声检验结果为：",LB(data['股价'], lags= 1))
'''利用单位根(ADF)进行平稳性检验'''
from statsmodels.tsa.stattools import adfuller as ADF
print("ADF平稳性检验结果为：",ADF(data['股价']))
'''
LB检验 p值：1.72947396e-09，远小于0.05的显著水平，说明此间序列远不是随机的白噪声
ADF输出结果，p值远大于0.05显著水平，该序列为非平稳序列
-1.1405685913236308为ADF值；0.6986255799201112为p值；
{'1%': -3.626651907578875, '5%': -2.9459512825788754, '10%': -2.6116707716049383}为cValue值
'''

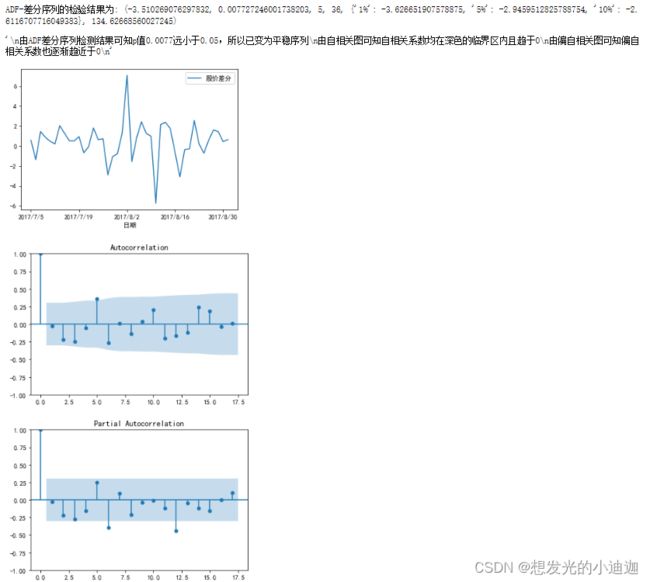
'''Step3：由于ADF平稳性检测出此为非平稳序列，所以借助n次差分运算将非平稳序列转换为平稳序列'''

'''对原始数据进行一阶差分,并删除其中含有缺失值的行(删除非法值)，原始数据对应变为差分数据，但列索引名仍为“股价”'''
D_data= data.diff().dropna()
'''将列索引名“股价”改为“股价差分”'''
D_data.columns= ['股价差分']
'''画出差分后的时序图'''
D_data.plot()
'''差分后的自相关图'''
plot_acf(D_data)
'''差分后的偏自相关图'''
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data, method='ywm')

'''对差分后的差分序列进行平稳性检验'''
print('ADF-差分序列的检验结果为:',ADF(D_data[u'股价差分']))

'''
由ADF差分序列检测结果可知p值0.0077远小于0.05，所以已变为平稳序列
由自相关图可知自相关系数均在深色的临界区内且趋于0
由偏自相关图可知偏自相关系数也逐渐趋近于0
'''

'''Step4：根据AIC信息准则定阶：确定模型参数的最优p、q值'''
from statsmodels.tsa.arima.model import ARIMA
data['股价']= data['股价'].astype(float)
'''设置模型参数p、q的最大值范围'''
pmax= int(len(D_data)/10)#阶数不超过length/10
qmax= int(len(D_data)/10)#阶数不超过length/10
e_matrix= []#定义空列表，作为评价矩阵,存储所有的p、q值
for p in range(pmax+1):
    tmp= []#空列表，暂存ARIMA模型的p、q值
    for q in range(qmax+1):
        '''因为存在部分报错，所以报错部分用try跳过执行except部分'''
        try:
            tmp.append(ARIMA(data,order= (p,1,q)).fit().aic)
        except:
            tmp.append(None)
    e_matrix.append(tmp)
'''将e_matrix列表转换为表格形式'''
e_matrix= pd.DataFrame(e_matrix)
'''用stcak将展平，然后找出最小值的位置赋给p.q'''
p,q= e_matrix.stack().idxmin()
'''最小的AIC对应的p和q值为最佳的阶数'''
print('最小的AIC对应的p和q值为：%s、%s'%(p,q))
	>>> AIC最小的p和q值为：4、3

'''Step5：使用ARIMA(4,1,3)模型对股票进行预测'''
arima= ARIMA(data, order= (p,1,q)).fit()
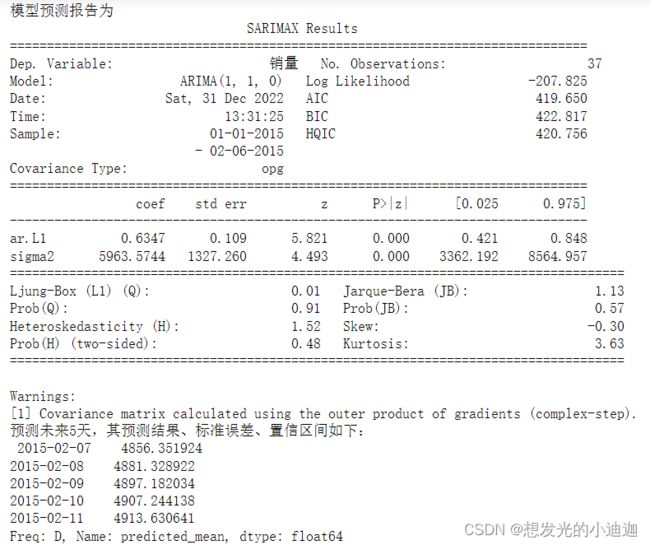
print('模型预测报告为\n',arima.summary())
'''model.forecast(5)#对未来5天进行预测'''
print('预测未来5天，其预测结果、标准误差、置信区间如下：\n', arima.forecast(5))

完整代码如下：

'''Step1：数据处理并显示数据的折线图'''
import pandas as pd
import matplotlib.pyplot as plt
'''设置中文字体，使中文能够正常显示'''
plt.rcParams['font.sans-serif']= ['SimHei']
'''正常显示正负号'''
plt.rcParams['axes.unicode_minus']= False
data= pd.read_csv('E:\data\stockClose.csv', index_col= '日期', encoding= 'ANSI')
'''xlim=[0,42]代表x轴刻度从0到42共有43个刻度'''
data.plot(title= '7~8月份股价', xlim= [0,42])
plt.xlabel('日期')
plt.ylabel('股价(美元)')
plt.show()
'''Step2：纯随机性和平稳性检验并画出股票数据的自相关图并输出纯随机性LB检验和ADF检验的结果'''
'''画自相关图'''
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data)
'''利用LB统计量进行白噪音检验'''
from statsmodels.stats.diagnostic import acorr_ljungbox as LB
print("白噪声检验结果为：",LB(data['股价'], lags= 1))
'''利用单位根(ADF)进行平稳性检验'''
from statsmodels.tsa.stattools import adfuller as ADF
print("ADF平稳性检验结果为：",ADF(data['股价']))
'''
LB检验 p值：1.72947396e-09，远小于0.05的显著水平，说明此间序列远不是随机的白噪声
ADF输出结果，p值远大于0.05显著水平，该序列为非平稳序列
-1.1405685913236308为ADF值；0.6986255799201112为p值；
{'1%': -3.626651907578875, '5%': -2.9459512825788754, '10%': -2.6116707716049383}为cValue值
'''
'''Step3：由于ADF平稳性检测出此为非平稳序列，所以借助n次差分运算将非平稳序列转换为平稳序列'''

'''对原始数据进行一阶差分,并删除其中含有缺失值的行(删除非法值)，原始数据对应变为差分数据，但列索引名仍为“股价”'''
D_data= data.diff().dropna()
'''将列索引名“股价”改为“股价差分”'''
D_data.columns= ['股价差分']
'''画出差分后的时序图'''
D_data.plot()
'''差分后的自相关图'''
plot_acf(D_data)
'''差分后的偏自相关图'''
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data, method='ywm')

'''对差分后的差分序列进行平稳性检验'''
print('ADF-差分序列的检验结果为:',ADF(D_data[u'股价差分']))

'''
由ADF差分序列检测结果可知p值0.0077远小于0.05，所以已变为平稳序列
由自相关图可知自相关系数均在深色的临界区内且趋于0
由偏自相关图可知偏自相关系数也逐渐趋近于0
'''
'''Step4：根据AIC信息准则定阶：确定模型参数的最优p、q值'''
from statsmodels.tsa.arima.model import ARIMA
data['股价']= data['股价'].astype(float)
'''设置模型参数p、q的最大值范围'''
pmax= int(len(D_data)/10)#阶数不超过length/10
qmax= int(len(D_data)/10)#阶数不超过length/10
e_matrix= []#定义空列表，作为评价矩阵,存储所有的p、q值
for p in range(pmax+1):
    tmp= []#空列表，暂存ARIMA模型的p、q值
    for q in range(qmax+1):
        '''因为存在部分报错，所以报错部分用try跳过执行except部分'''
        try:
            tmp.append(ARIMA(data,order= (p,1,q)).fit().aic)
        except:
            tmp.append(None)
    e_matrix.append(tmp)
'''将e_matrix列表转换为表格形式'''
e_matrix= pd.DataFrame(e_matrix)
'''用stcak将展平，然后找出最小值的位置赋给p.q'''
p,q= e_matrix.stack().idxmin()
'''Step5：使用ARIMA(4,1,3)模型对股票进行预测'''
arima= ARIMA(data, order= (p,1,q)).fit()
print('模型预测报告为\n',arima.summary())
'''model.forecast(5)#对未来5天进行预测'''
print('预测未来5天，其预测结果、标准误差、置信区间如下：\n', arima.forecast(5))

思考与练习2

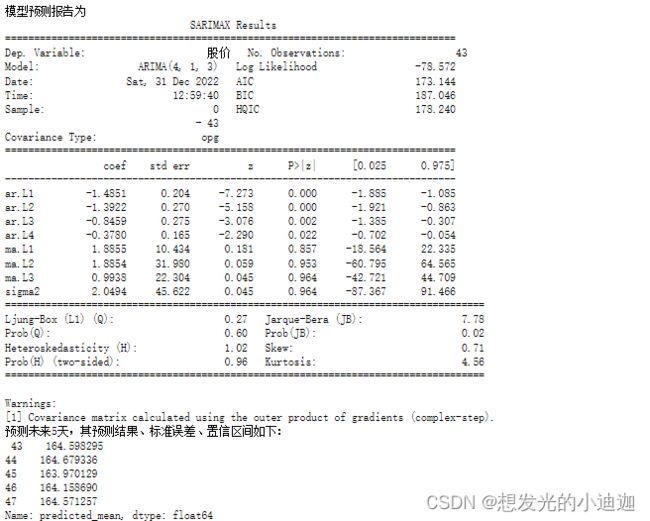
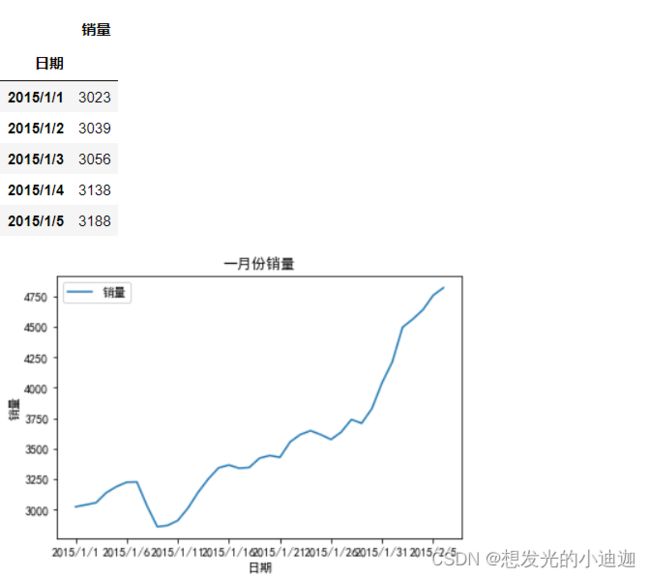
文件shop.csv是某商店的销售记录，仿照例8-2对其１月份数据进行ARIMA建模分析，对２月份前５天的销售额进行预测，并与实际结果比较。

import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']= ['SimHei']
plt.rcParams['axes.unicode_minus']= False
data= pd.read_csv(r'E:\data\shop.csv', index_col= 0,encoding= 'ANSI')
display(data.head())
data.plot(title= '一月份销量')
plt.xlabel('日期')
plt.ylabel('销量')
plt.show()

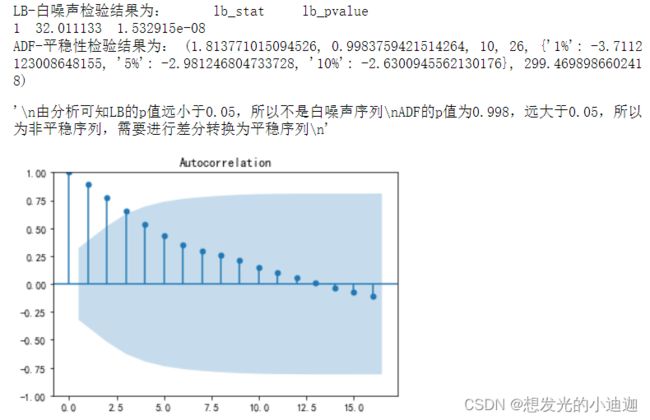
#画出原始数据的自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data)
from statsmodels.stats.diagnostic import acorr_ljungbox as LB
print("LB-白噪声检验结果为：",LB(data['销量'],lags= 1))
from statsmodels.tsa.stattools import adfuller as ADF
print("ADF-平稳性检验结果为：",ADF(data['销量']))
'''
由分析可知LB的p值远小于0.05，所以不是白噪声序列
ADF的p值为0.998，远大于0.05，所以为非平稳序列，需要进行差分转换为平稳序列
'''

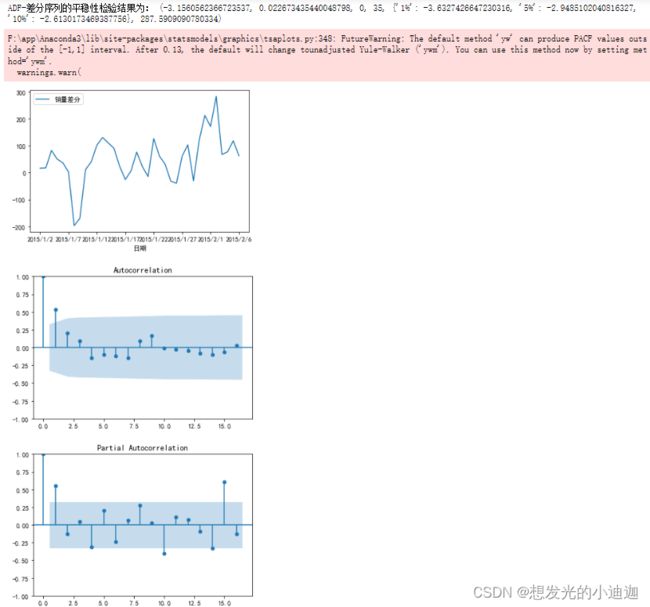
D_data= data.diff().dropna()#进行一阶差分并删除非法值
D_data.columns= ['销量差分']#更改列索引名
D_data.plot()#销量差分后的时序图
plot_acf(D_data)#差分后的自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data)
print("ADF-差分序列的平稳性检验结果为：",ADF(D_data[u'销量差分']))
'''
由分析可知，差分序列的p值为0.022，小于0.05，所以为平稳序列
'''

from statsmodels.tsa.arima.model import ARIMA
data['销量']= data['销量'].astype(float)
'''设置模型参数p、q的最大值范围'''
pmax= int(len(D_data)/10)#阶数不超过length/10
qmax= int(len(D_data)/10)#阶数不超过length/10
e_matrix= []#定义空列表，作为评价矩阵,存储所有的p、q值
for p in range(pmax+1):
    tmp= []#空列表，暂存ARIMA模型的p、q值
    for q in range(qmax+1):
        '''因为存在部分报错，所以报错部分用try跳过执行except部分'''
        try:
            tmp.append(ARIMA(data,order= (p,1,q)).fit().aic)
        except:
            tmp.append(None)
    e_matrix.append(tmp)
'''将e_matrix列表转换为表格形式'''
e_matrix= pd.DataFrame(e_matrix)
'''用stcak将展平，然后找出最小值的位置赋给p.q'''
p,q= e_matrix.stack().idxmin()
'''最小的AIC对应的p和q值为最佳的阶数'''
print('最小的AIC对应的p和q值为：%s、%s'%(p,q))
	>>> 最小的AIC对应的p和q值为：1、0

model= ARIMA(data, order= (p,1,q)).fit()
print('模型预测报告为\n',model.summary())
'''model.forecast(5)#对未来5天进行预测'''
print('预测未来5天，其预测结果、标准误差、置信区间如下：\n', model.forecast(5))

非线性模型

有些序列成因及其复杂，则需要采用非线性模型。

非线性模型包括：岭核回归模型和神经网络模型

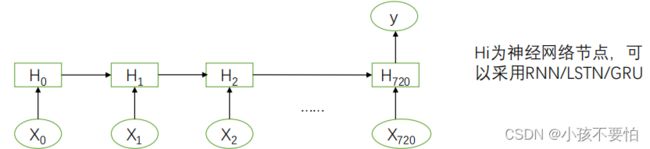
神经网络模型

用平均绝对误差(MAE)指标评估模型性能

• 深度神经网络处理序列数据的方法：
  （1）循环神经网络（RNN）：基于RNN(即SimpleRNN)的RNN、基于LSTM的RNN、基于GRU的RNN
  （2）一维卷积神经网络（1D convent）
  注意三种循环神经网络方式区别:
  RNN参数最少，长序列预测能力差
  LSTM（长短期记忆）模型复杂，参数最多，需要训练的数据也多
  GRU（门控制单元）是简化的LSTM，运行的计算代价相对较低
  

Keras.layers.recurrent提供了SimpleRNN、LSTM、GRN

from keras.layers import LSTM
LSTM_layer=LSTM(units, input_dim, return_sequence, input_length, dropout, recurrent_dropout)
参数说明如下：

参数	解释
units	输出维度
input_dim等同于input_shape	输入维度，当使用该层为模型首层时，应该指定该值
return_sequence	默认为False.若为True返回整个序列每个节点的输出，否则只返回最后一个节点输出
input_length	输入长度固定时候，表示序列的长度，若该层为全连接层，则必须指定

循环神经网络模型相关代码：

• 神经网络模型初始化：
  from keras.models import Sequential
model= Sequential()
• 将循环神经网络模型的三种方式中的以一个加入到模型中，此处以LSTM为例
  model.add(LSTM(32,input_shape=(None,X.shape[-1])))—将输入的低维数据转换为高维（32）并输出到神经网络的神经网络层中进行处理，为神经网络模型首层
  model.add(Dense(units))------为model添加神经网络层并且定义神经网络层中的神经元数为units
• 配置训练方法，告知训练时用的优化器、损失函数和准确率评测标准
  model.compile(optimizer， loss，metrics)
• 模型学习
  model.fit(X, y, enochs, batch_size, validation_split)
  参数解释如下：

参数	解释
Dense (units)	Dense为神经网络模型添加神经网络层；units为神经网络层添加神经元，此为神经元的个数
optimizer	训练时用的优化器
loss	训练时用的损失函数
metrics	训练时的准确率评测标准
enochs	完整数据集通过神经网络一次并且返回一次的过程称为一个epochs ，若epochs=5,则数据被神经网络学习5次
batch_size	表示单次传递给程序用以训练的数据（样本）个数，比如我们的训练集有1000个数据。这是如果我们设置batch_size=100，那么程序首先会用数据集中的前100个参数，即第1-100个数据来训练模型。当训练完成后更新权重，再使用第101-200的个数据训练，直至第十次使用完训练集中的1000个数据后停止。
validation_split	在没有提供验证集的时候，按一定比例从训练集中取出一部分作为验证集

例题8-3相关重要代码如下：

• 构建基于SimPleRNN或LSTM或GRU的神经网络并编译(用到哪个将哪个导入即可)
  from keras.models import Sequential
from keras.layers import Dense,LSTM,SimpleRNN,GRU
model= Sequential()—神经网络模型初始化
  model.add(LSTM(32,input_shape=(None,X.shape[-1])))—将输入的低维数据转换为高维（32）并输出到神经网络的神经网络层中进行处理，为神经网络模型的首层
  model.add(Dense(1))------为model添加神经网络层，并设置神经网络层中的神经元的个数为1
• 在配置训练方法时，告知训练时用的优化器、损失函数
  from keras.optimizers import RMSprop
model.compile(optimizer=RMSprop(),loss='mae')—损失函数为平均绝对误差,用来预测温度、回归问题。
• 模型学习
  model.fit(X, y, enochs= 5, batch_size= 128, validation_split= 0.2)
• 查看前五条预测值
  tt=np.zeros((y_predict.shape[0],14))
for i in range(y_predict.shape[0]):
  -------tt[i,0]=y_predict[i,0]
ss.inverse_transform(tt)[:,0][0:5]

注意：
ss= StandardScaler()数据标准化
ss.inverse.transform()反标准化，将预测后的标准化数据变为标准化之前的数据，即为预测值

例题8-3：基于LSTM的温度时序预测


注意：构造样本数据集比较特殊，在例题中已进行展示并对代码进行解释

'''Step1:1从文件中读出数据并进行数据预处理'''
import pandas as pd
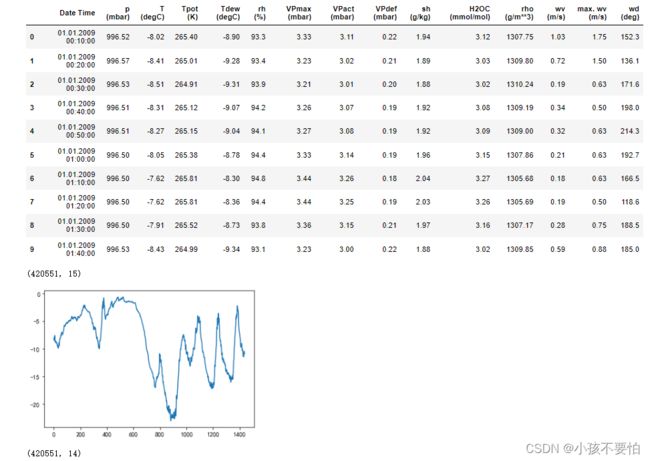
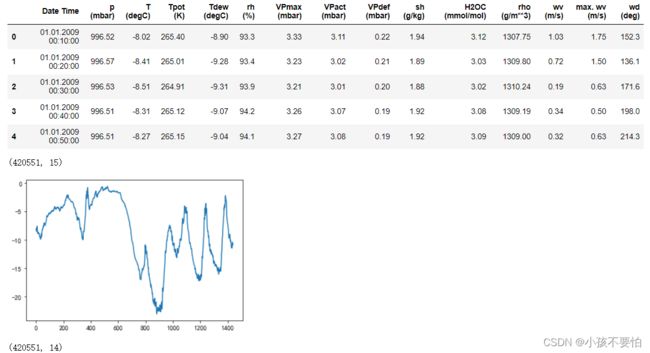
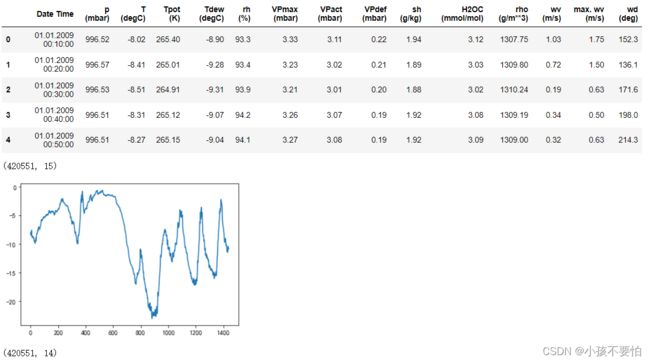
data= pd.read_csv(r'E:\data\jena_climate_2009_2016.csv')
display(data.head(10))
display(data.shape)
#T (degC)为温度
#用10天的温度绘制时间序列图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']= ['SimHei']
plt.rcParams['axes.unicode_minus']= False
temp=data["T (degC)"]
temp_10days= temp[:1440]#前十天共有1440个数据节点
temp_10days.plot()
plt.show()
#数据标准化
from sklearn.preprocessing import StandardScaler
ss= StandardScaler()
data_process= data.drop('Date Time',axis = 1)
data_process= ss.fit_transform(data_process)#数据标准化
display(data_process.shape)
display(data_process)
data_process[2,:][1]

运行结果显示为：

'''
Step2:随机从序列中选择5000个子序列，每个子序列长度为721，构造样本数据集
'''
import numpy as np
sample= 5000#原数据shape为（420551，15）
'''
由文件数据可知一个小时内有6个数据点，一天24小时，所以一天的数据有24*6，则五天共有5*24*6
'''
lookback= 5*24*6 #720个数据节 前5天数据
delay=24*6 #144条数据 后一天数据
'''
#X为三维数组 形状（samples, inputlength, input_dim)
samples表示样本数，input_length = lookback 每个样本包含的数据点 数据点=天数*24小时/天
*6 数据点/小时, input_dim = 14 第三维是每个数据点包含的特征数
'''
# y为1D数组，形状（samples），温度
#data_process.shape[-1]代表求出data_process的维数然后取其列数
#X：生成五千个lookback行data_process.shape[-1]列元素全为0的数组
X= np.zeros((sample,lookback,data_process.shape[-1]))#(5000,720,14)
y=np.zeros((sample,))#生成一个元素均为0，元素个数为sample的一维数组

#2.1随机生成5000个时刻 前5天后1天的数据存在
'''最小的数组下标索引---记第六天的第一个数据点元素下标为最小值的索引值'''
min_index= lookback#720
'''
#因为数组下标从0开始，所以需要减去1才为后一天数据
#最大的数组下标索引---记最后一天的第一个数据点元素的下标为最大值索引值
'''
max_index= len(data_process)-delay-1#420511-144-1
#np.random.randint(start,end,size)—随机生成给定范围内的一组整数
#随机生成[min_index,max_index)范围内的元素个数为sample的一组整数
rows= np.random.randint(min_index,max_index,size=sample)
#为这5000个时刻生成x和y数据
'''enumerate()为内置函数，依次遍历rows一维数组内的每个元素,j为元素下标，row为元素值'''
for j ,row in enumerate(rows):
    #创建一个一维数组，数组元素范围为[row-lookback,row)
    indices= np.arange(row-lookback,row)
    #将data_process中对应行的数据存入X的第j个数组中
    X[j]=data_process[indices,:]
    X[j]=data_process[row+delay,:][1]

'''Step3：构建基于LSTM的神经网络并编译'''
from keras.models import Sequential
from keras.layers import Dense,LSTM
model= Sequential()
'''
神经网络模型-LSTM模型初始化
LSTM输出维度为32，也就是将输入14维的特征转换为32维的特征。
模型只使用一层LSTM，只需要返回最后结点的输出
X.shape[-1]是最后轴的维度大小14
units= 32---输出维度
input_dim即输入维度，当使用该层为模型首层时，应该指定该值（或等价的指定input_shape）
'''
#将输入的低维数据转换为高维（32）并输出到神经网络的神经网络层中进行处理，为神经网络模型的首层
model.add(LSTM(32,input_shape=(None,X.shape[-1])))
model.add(Dense(1))为model添加神经网络层，并设置神经网络层中的神经元的个数为1

#模型只预测1个温度值，全连接层输出结点数为1; 回归问题不使用激活函数
#神经网络编译
from keras.optimizers import RMSprop
'''
model.compile()：在配置训练方法时，告知训练时用的优化器、损失函数
#损失函数为平均绝对误差（MAE），用来预测温度、回归问题
'''
model.compile(optimizer=RMSprop(),loss='mae')
'''
#神经网络训练
#epochs------完整数据集通过神经网络一次并且返回一次的过程称为一个epochs
#此处epochs=5,则数据被神经网络学习5次
batch_size=128------单次传递给程序用以训练的数据（样本）个数
validation_split=0.2------在没有提供验证集的时候，按一定比例从训练集中取出一部分作为验证集
'''
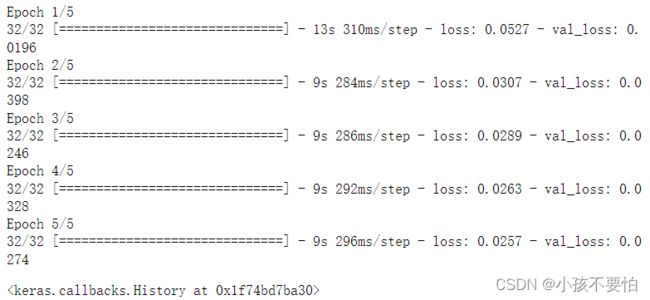
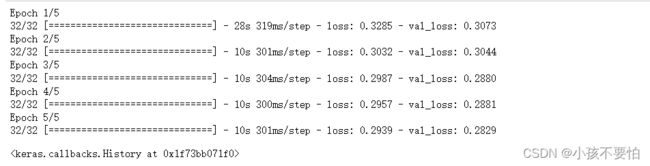
model.fit(X,y,epochs=5,batch_size=128,validation_split=0.2)

运行结果显示为：

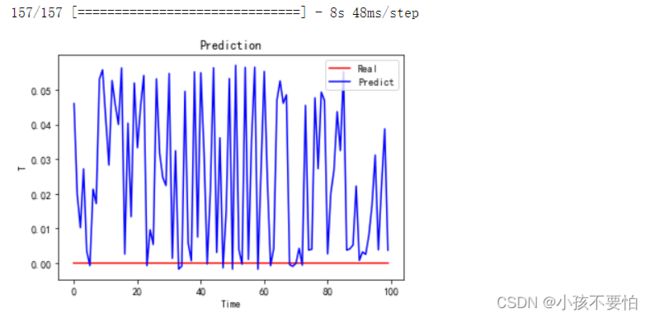
#4对比预测结果---前100条数据
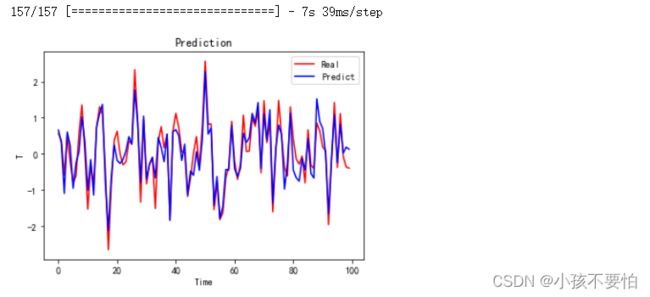
y_predict=model.predict(X)
plt.plot(y[0:100], color='red', label='Real')
plt.plot(y_predict[0:100], color='blue', label='Predict')
plt.title(label='Prediction')
plt.xlabel(xlabel='Time')
plt.ylabel(ylabel='T')
plt.legend()
plt.show()

运行结果显示为：

```python
#5查看前五条预测值
#创建一个y_predict.shape[0]行，14列且元素均为0的数组
tt=np.zeros((y_predict.shape[0],14))
#tt[:,0]=tt[:,0]+y_predict #构造包含14列数据的对象，便于数据恢复
for i in range(y_predict.shape[0]):
    #将预测的结果均存在数组tt中
    tt[i,0]=y_predict[i,0]
'''
ss= StandardScaler()数据标准化
ss.inverse.transform()反标准化，将预测后的标准化数据变为标准化之前的数据，即为预测值
[:,0]取tt的预测值那一列
[0:5]显示预测值的前五行数据

'''
ss.inverse_transform(tt)[:,0][0:5]

运行结果显示为：

思考与练习3

第一题：尝试将例9-2例深度学习模型的LSTM层分别替换为SimpleRNN、GRU层，分析预测误差并与使用LSTM层的结果进行比较

import pandas as pd
import matplotlib.pyplot as plt
data= data= pd.read_csv(r'E:\data\jena_climate_2009_2016.csv')
display(data.head())
display(data.shape)
#绘制前10天的温度时间序列图
plt.rcParams['font.sans-serif']= ['SimHei']
plt.rcParams['axes.unicode_minus']= False
temp= data["T (degC)"]
temp_10days= temp[:1440]
temp_10days.plot()
plt.show()
from sklearn.preprocessing import StandardScaler
ss= StandardScaler()
data_process= data.drop('Date Time',axis = 1)
'''
注意：删除时间这一列之后，温度变为下标为1的这一列
'''
data_process= ss.fit_transform(data_process)
display(data_process.shape)

import numpy as np
sample= 5000#选择5000个子序列构造样本集
lookback= 5*24*6#前5天的数据
delay= 24*6#后一天的数据
X= np.ones((sample, lookback, data_process.shape[-1]))
y= np.ones((sample),)
min_index= lookback#记第六天的第一个数据点元素的下标为最小值索引值
max_index= len(data_process)- delay-1#记最后一天的第一个数据点元素的下标为最大值索引值
rows= np.random.randint(min_index, max_index, sample)
for j, row in enumerate(rows):
    indices= np.arange(row-lookback, row)
    X[j]= data_process[indices,:]
    y[j]= data_process[row+delay,:][1]#温度所在列的下标为1,将温度值赋给y

构建SimpleRNN神经网络并编译

#构建SimpleRNN神经网络并编译
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN
'''
神经网络模型-SimpleRNN模型初始化
'''
model= Sequential()
#将14维数据转换为32维输出
model.add(SimpleRNN(32, input_shape= (None, X.shape[-1])))
model.add(Dense(1))

from keras.optimizers import RMSprop
model.compile(optimizer= RMSprop(), loss= 'mae')
#神经网络模型-SimpleRNN模型训练
model.fit(X, y, epochs= 5, batch_size= 128, validation_split= 0.2)

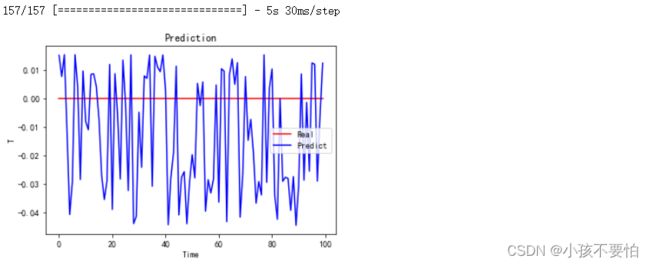
y_predict= model.predict(X)
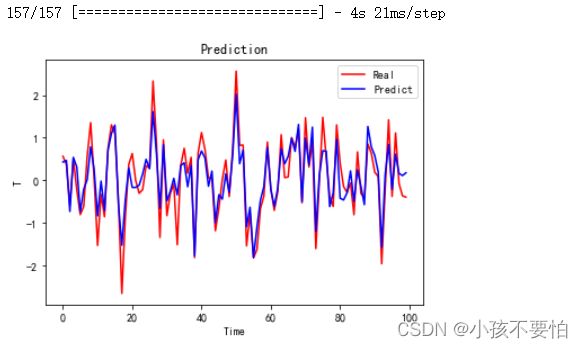
plt.plot(y[0:100],c= 'r', label= 'Real')
plt.plot(y_predict[0:100], c= 'b', label= 'Predict')
plt.title(label='Prediction')
plt.xlabel(xlabel='Time')
plt.ylabel(ylabel='T')
plt.legend()
plt.show()

tt= np.zeros((y_predict.shape[0],14))
for i in range(y_predict.shape[0]):
    tt[i,0]= y_predict[i,0]
ss.inverse_transform(tt)[:,0][0:5]
	>>> array([992.81532178, 993.12451122, 983.11625766, 993.72503323,991.83320315])

构建GRU神经网络并编译

from keras.models import Sequential
from keras.layers import Dense, GRU
model1= Sequential()
model1.add(GRU(32,input_shape= (None, X.shape[-1])))
model1.add(Dense(1))
from keras.optimizers import RMSprop
model1.compile(optimizer= RMSprop(), loss= 'mae')
model1.fit(X, y, epochs= 5, batch_size= 128, validation_split= 0.2)

y_predict1= model1.predict(X)
plt.plot(y[0:100], c= 'r', label= 'Real')
plt.plot(y_predict1[0:100], c= 'b', label= 'Predict')
plt.title(label='Prediction')
plt.xlabel(xlabel='Time')
plt.ylabel(ylabel='T')
plt.legend()
plt.show()

tt1= np.zeros((y_predict1.shape[0], 14))
for i in range(y_predict1.shape[0]):
    tt1[i,0]= y_predict1[i, 0]
ss.inverse_transform(tt1)[:,0][0:5]
	>>> array([994.69903737, 991.74323903, 980.08548639, 994.28712606,991.13820815])

第二题：如果使用前3天的天气信息预测未来12小时后的温度，尝试生成训练样本数据，建立预测模型，分析预测误差。

import pandas as pd
import matplotlib.pyplot as plt
data= data= pd.read_csv(r'E:\data\jena_climate_2009_2016.csv')
display(data.head())
display(data.shape)
#绘制前10天的温度时间序列图
plt.rcParams['font.sans-serif']= ['SimHei']
plt.rcParams['axes.unicode_minus']= False
temp= data["T (degC)"]
temp_10days= temp[:1440]
temp_10days.plot()
plt.show()
from sklearn.preprocessing import StandardScaler
ss= StandardScaler()
data_process= data.drop('Date Time',axis = 1)
'''
注意：删除时间这一列之后，温度变为下标为1的这一列
'''
data_process= ss.fit_transform(data_process)
display(data_process.shape)

#2随机从序列中选择5000个子序列，每个子序列长度为721，构造样本数据集
import numpy as np
sample= 5000#原数据shape为（420551，15）
'''
由文件数据可知一个小时内有6个数据，一天24小时，所以一天的数据有24*6，则五天共有5*24*6
'''
lookback= 3*24*6 #432个数据节 前3天数据
delay=24*6 #144条数据 后一天数据
#X为三维数组 形状（samples, inputlength, input_dim)
'''
samples表示样本数，input_length = lookback 每个样本包含的数据点 数据点=天数*24小时/天
*6 数据点/小时, input_dim = 14 第三维是每个数据点包含的特征数
'''
# y为1D数组，形状（samples），温度
#data_process.shape[-1]代表求出data_process的维数然后取其列数
#X：生成五千个lookback行data_process.shape[-1]列元素全为0的数组
X= np.zeros((sample,lookback,data_process.shape[-1]))#(5000,720,14)
y=np.zeros((sample,))#生成一个元素均为0，元素个数为sample的一维数组

#2.1随机生成5000个时刻 前3天后1天的数据存在
#最小的数组下标索引---记第六天的第一个数据点元素下标为最小值的索引值
min_index= lookback#432
#因为数组下标从0开始，所以需要减去1才为后一天数据
#最大的数组下标索引---记最后一天的第一个数据点元素的下标为最大值索引值
max_index= len(data_process)-delay-1#420511-144-1
#np.random.randint(start,end,size)—随机生成给定范围内的一组整数
#随机生成[min_index,max_index)范围内的元素个数为sample的一组整数
rows= np.random.randint(min_index,max_index,size=sample)
#为这5000个时刻生成x和y数据
#enumerate()为内置函数，依次遍历rows一维数组内的每个元素,j为元素下标，row为元素值
for j ,row in enumerate(rows):
    #创建一个一维数组，数组元素范围为[row-lookback,row)
    indices= np.arange(row-lookback,row)
    #将data_process中对应行的数据存入X的第j个数组中
    X[j]=data_process[indices,:]
    X[j]=data_process[row+delay,:][1]

#3构建基于LSTM的神经网络并编译
from keras.models import Sequential
from keras.layers import Dense,LSTM
model2= Sequential()
'''
神经网络模型-LSTM模型初始化
LSTM输出维度为32，也就是将输入14维的特征转换为32维的特征。
模型只使用一层LSTM，只需要返回最后结点的输出
X.shape[-1]是最后轴的维度大小14
units= 32,
input_dim即输入维度，当使用该层为模型首层时，应该指定该值（或等价的指定input_shape）
'''
#将输入的14维转换为32维输出
model2.add(LSTM(32,input_shape=(None,X.shape[-1])))
model2.add(Dense(1))

#模型只预测1个温度值，全连接层输出结点数为1; 回归问题不使用激活函数
#神经网络编译
from keras.optimizers import RMSprop
#损失函数为平均绝对误差（MAE） 预测温度、回归问题
model2.compile(optimizer=RMSprop(),loss='mae')
#神经网络训练
model2.fit(X,y,epochs=5,batch_size=128,validation_split=0.2)

#4对比预测结果---前100条数据
y_predict2=model2.predict(X)
plt.plot(y[0:100], color='red', label='Real')
plt.plot(y_predict2[0:100], color='blue', label='Predict')
plt.title(label='Prediction')
plt.xlabel(xlabel='Time')
plt.ylabel(ylabel='T')
plt.legend()
plt.show()

#5查看前五条预测值
#创建一个y_predict2.shape[0]行，14列且元素均为0的数组
tt2=np.zeros((y_predict2.shape[0],14))
#tt2[:,0]=tt[:,0]+y_predict2 #构造包含14列数据的对象，便于数据恢复
for i in range(y_predict2.shape[0]):
    #将预测的结果均存在数组tt中
    tt2[i,0]=y_predict2[i,0]
'''
ss= StandardScaler()数据标准化
ss.inverse.transform()反标准化，将预测后的标准化数据变为标准化之前的数据，即为预测值
[:,0]取tt2的预测值那一列
[0:5]显示预测值的前五行数据

'''
ss.inverse_transform(tt2)[:,0][0:5]
	>>> array([989.33805878, 989.2758882 , 989.34020193, 989.11247105,988.8716126 ])

语音识别技术(ASR)

定义：让机器通过识别和理解语音信号的过程，是把语音信号转变为相应文本或命令。

语音数据采样

语音数据是一种典型的时序数据，它通过对连续声音信号的振幅进行固定频率采样，实时转换为离散时间序列
常用音频采用频率有44.1Hz、48kHz和192kHz等
数据量庞大，处理复杂

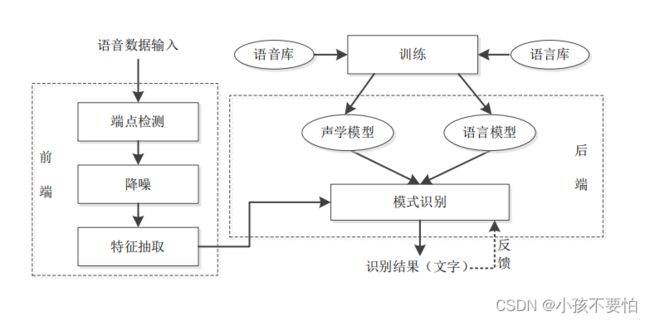
语音识别基本框架

语音识别中的时序数据处理

• 预处理
  降噪和语音断点检测
• 分帧
  将语音切割成按时间顺序排列、等长的语音段，每一段称为一帧
  通常相邻的语音帧之间有交叠
• 特征提取—常用的特征是梅尔倒谱系数MFCC
  由于波形在时域上的描述能力有限，所以需要对语音帧进行变换，提取较容易识别的声学特征。
• 语音识别
  采用音素作为识别单元
  音素是构成单词发音的基本单位

需安装baidu-aip库
语音识别初始化：
aip= AipSpeech(APP_ID, API_KKEY, SECRET_KEY)
语音识别：
result= aip.asr(speech, format, rate, {‘dev_pid’:code},…)
参数解释如下：

参数	解释
speech	建立包含语音内容的Buffer对象
format	语音文件格式，pcm(不压缩)、wav、amr
rate	采样率，16000，固定值
dev_pid	语言类型。1536：普通话；1537：带标点的普通话；1736：英语；1636：粤语；1836：四川话

例题8-4：使用百度语音开放平台识别一段语音文件对应的文字

#导入语音包
from aip import AipSpeech
#从文件中提取语音内容,建立包含语音内容的Buffer对象
def get_file_content(file_name):
    with open(file_name, 'rb') as fp:
        return fp.read()
APP_ID = ''
API_KEY = ''
SECRET_KEY = ''
#语音识别模型初始化
aip= AipSpeech(APP_ID, API_KEY, SECRET_KEY)
file_name= 'E:\data/voice.wav'
result= aip.asr(get_file_content(file_name), 'wav', 16000, {'dev_pid':1536})
print(result['result'][0])

运行结果显示为：