灰度变换和空间滤波
灰度变换和空间滤波
- 灰度变换
-
- 灰度变换和空间滤波基础
- 一些基本的灰度变换函数
-
- 图像反转
- 对数变换
- 幂律(伽马)变换
- 分段线性变换函数
-
- 对比度拉伸
- 灰度级分层
- 比特平面分层
- 直方图处理
-
- 直方图均衡化
- 直方图匹配(规定化)
-
- 连续的直方图匹配(规定化)
- 离散的直方图匹配(规定化)
- 直方图规定化的应用
- 局部直方图处理
-
- “块状”效应
- 使用直方图统计量增强图像
- 空间滤波
-
- 空间滤波基础
-
- 线性空间滤波的原理
- 空间相关与卷积
- 可分离滤波器核
- 空间域滤波和频率域滤波的一些重要比较
- 平滑(低通)空间滤波器
灰度变换
本节讨论的是空间域技术,空间域技术直接操作图像中的像素,频率域技术操作的是图像的傅里叶变换而非图像本身。
灰度变换和空间滤波基础
1.空间域处理基于表达式
f(x,y)是输入图像,g(x,y)是输出图像,T是在点(x,y)的一个邻域上定义的针对f的算子。
例如:算子T被定义为“计算邻域内像素的平均灰度”
T也可称为灰度变换函数(也称灰度级或映射):
当算子的邻域位于图像外部时,解决方案有两种:
(1)忽略图像外部的值;
(2)填充图像(更为可取)
一些基本的灰度变换函数
主要介绍3类基本函数:线性(反转和恒等变换)函数、对数(对数和反对变换)函数和幂律(n次幂和n次根变换)函数
图像反转
灰度级在区间[0,L-1]内的反转图像形式为:
这种处理可用于增强图像暗色区域的白色或灰色细节,暗色区域的尺寸很大时这种增强效果很好。
对数变换
对数变换的通式为:
c是一个常数,并假设r≥0.
这个变换将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度级。相反,输入中的高灰度值则被映射为输出中范围较窄的灰度级,使用这类变换来扩展图像中的暗像素值,同时压缩高灰度级值。反对数(指数)变换的功能正好相反。
这里跟图像反转的区别是对数变换的高灰度级像素只是被压缩,不至于像图像反转被反转称暗色,目的是提高低灰度值区域的细节,但也保留高灰度值区域的主要特征。
幂律(伽马)变换
幂律变换的形式为
s=cry
c和y是正常数。
像对数变换那样,幂律曲线用分数值y将较窄范围的暗输入值映射为较宽范围的输出值,将高输入值映射为较宽范围的输出值。y>1生成的曲线与y<1生成的曲线效果正好相反。c=y=1时,此时曲线表示的变换为恒等变换。
分段线性变换函数
对比度拉伸
灰度级分层
一种方法时将感兴趣范围内的所有灰度值显示为一个值,而将所有其他灰度值显示为另一个值,这种变换产生一幅二值图像。另一种方法是使期望的灰度范围变亮(或变暗),但保持图像中的其他灰度级不变。
如下图:

比特平面分层
像素值是由比特组成的整数,在一幅256级灰度图像中,图像值是由8比特(1字节)组成的。

8比特图像的第8个比特平面的二值图像可用一个变换函数阈值处理输入图像得到,这个变换将0到127之间的灰度值映射为0,将128到255之间的灰度值映射为1.
8比特图像的第7个比特平面的二值图像可将0到63之间的灰度值映射为0,将64到127之间的灰度值映射为1得到.
通常只要存储高位的比特平面就可以还原出和原图像近似的可接受的图像,这种方法可以减少存储需求。
直方图处理
令rk ,k=0,1,2,…,L-1表示一幅L级灰度数字图像f(x,y)的灰度。f的非归一化直方图定义为
h(rk)=nk,k=0,1,2,…,L-1
式中,nk是f中灰度为rk的像素的数量,并且细分的灰度级成为直方图容器。
类似地,f的归一化直方图定义为
p(rk)=h(rk)/MN=nk/MN
式中,M和N分别是图像的行数和列数。将这种直方图成为直方图或者图像直方图。
对k所有的值,p(rk)的和总是1
事实上,p(rk)的分量是对图像中出现的灰度级的概率的估计。

直方图均衡化
假设灰度值最初是连续的(无限个灰度值)令变量r表示待处理图像的灰度。假设r的值域[0,L-1],r=0表示黑色,r=L-1表示白色。
关注如下变换(灰度映射):
s=T( r ),0≤r≤L-1
假设:
(a)T( r )在区间0≤r≤L-1上是一个单调递增函数
(b)对于0≤r≤L-1,有0≤T( r )≤L-1
逆变换
r=T-1(s),0≤s≤L-1
假设:
(a~)T( r )在区间0≤r≤L-1上是一个严格单调递增函数
(b~)对于0≤r≤L-1,有0≤T( r )≤L-1
(a)中T( r )单调递增的条件保证输出灰度值从不小于对应的输入值,从而防止因灰度反转而产生伪像
(b)保证输出灰度的范围与输入的范围相同,最后(a~)保证从s返回到r的映射是一对一映射的,防止出现歧义。

左图在映射时无法恢复,因为逆映射是一系列值。
通常严格单调的条件无法满足,即反变换可能是不唯一的,所幸的是,这个问题在离散情况下很容易解决。(离散问题从直方图匹配(直方图规定化)处解决,等下会看到如何解决)
图像灰度变换的概率密度函数关系:
详情请查阅我的另一篇博文:
数字图像处理 冈萨雷斯 (第四版) 图像灰度值概率密度函数
上述博文只讲了连续值的图像灰度变换,对于离散值,我们用概率与求和来代替概率密度函数与积分(单调性依旧保留),在数字图像中出现灰度级rk的概率近似为
pk(rk)=nk/MN
式中,MN是图像中的像素总数,nk表示灰度值为rk的像素数。
pk(rk),rk∈[0,L-1]通常成为归一化图像直方图
图像灰度变换的离散形式为
sk=T(rk)=(L-1)SUMkj=0(pj(rj),k=0,1,2,…,L-1
使用上式将输入图像中灰度级为rk的每个像素映射为输出图像中灰度级为sk的对应像素,就得到处理后的图像,这称为直方图均衡化或直方图线性化变换。
注意:这里用的灰度变换映射用的对概率密度函数的积分,得到的是累积分布函数,对于s=T(r)=P{X≤r},其中X是随机变量,这个随机变量X只是作用于概率密度和分布函数,表示输入灰度概率之间的关系,对于整个灰度变换而言,这个X≤r不起作用,表示的函数关系依旧是单个灰度输入对应单个灰度输出。
直方图匹配(规定化)
上述直方图均衡化在一些应用并不是合适的。特别地,我们能够规定待处理图像的直方图形状是有用的。用于生成具有规定直方图的图像的方法,称为直方图匹配或直方图规定化。
连续的直方图匹配(规定化)
考虑连续灰度r和z,将r和z当作PDF为pk( r )和pz(z)的随机变量来处理。
其中r和z分别表示输入图像和输出(处理后)图像的灰度级。
pk( r )由已知的输入图像计算得到,pz(z)是规定得PDF
s与r是通过T( r )相联系得,所以由s得到z得映射可以直接用r表示。
然而求G-1得解析表达式并不容易,但在使用离散量时不是问题,下一节会讲到离散情况的处理。

离散的直方图匹配(规定化)


离散化直方图匹配(规定化)中的反函数G-1除了满足自映射之外(已满足),还必须满足严格单调,对于离散化中的pz(zi)值不能为零,其中上述操作的步骤3能够解决这一“导致函数不严格单调”的问题。
注意:sk为输入直方图pr(r)经过直方图均衡化得到的,表格中存储的值为规定化直方图的灰度分布值G,查找表的操作是根据经过直方图均衡化后的输入图像灰度sk对应表格中的G值,找到对应的zq的值,使得G(zq)和sk最接近,并存储s➡z的映射,当多个zq对应的G值都匹配我们给的sk,我们选取最小的zq作为匹配的值。
直方图规定化的应用
例子:(直方图均衡化与直方图规定化的比较)
下图显示了一幅灰度级图像及其直方图,图像中有几个大的暗色区域,使得直方图中大量像素集中在灰度级的暗端(灰度级靠近0越暗,靠近255越亮)。背景中有一个目标,但很难分辨出它是什么。使用直方图的均衡化扩展直方图后,我们能看到暗色区域中的细节。


图3.24 (a)图(b)中的直方图得到的直方图均衡化灰度级变换函数;(b)直方图均衡化后的图像;(c)均衡化后的图像的直方图
如果目的只是简单地解释隐藏在图像暗色区域的内容,直方图均衡化能够实现这一目标,但是假设这幅图像要应用在光面杂志的出版,上述直方图均衡化后的图像中具有太多的噪声,原因是灰度级中一个非常窄的最暗端在输出图像中已扩展为更宽范围的灰度值。图3.24(c)中的直方图值已被压缩到灰度级的高值区域。
一般来说由于成像传感器在低亮度级的限制(暗感光能力差),图像中最暗区域的噪声是最大的,因此,直方图均衡化在这种情况下扩展了灰度级的最大噪声端,我们需要一个能够扩展灰度级低端的变换,但不是那么迫切,这是说明直方图规定话非常有用的一个典型案例。
直方图均衡化变换函数如此陡峭的原因是,输入图像直方图中有一个接近黑色的大峰值,因此合理的方法是修改直方图,使其不具有这样的性质。

图3.25 直方图规定化:(a)规定的直方图的PDF;(b)标为(1)的变换G(zq)和标为(2)的变换G-1(sk);©直方图规定化后的图像;(d)图像©的直方图
图3.25(a)显示了一个认为规定的函数,保留了原直方图的一般形状(暗像素分布与原图像相近),但是在灰度级的暗色区域中,灰度级的过渡更平滑(避免设备源的低亮度感知限制导致低亮度区域噪声过大)。
将该函数取样为256个等间隔的离散值,产生期望的规定直方图,使用上述讲过的离散直方图规定化中3.21式由这个规定的直方图PDF图(a)得到变换函数G(z)。在图3.25(b)中标为变换(1),上述讲过的离散直方图规定化中的3.23式得到反变换在图中标为变换(2)。
图3.25©中增强后的图像,是通过对图3.24(b)中直方图均衡化图像的像素sk应用变换(2)得到的(将均衡化的像素应用反变换得到规定化图像,sk➡zq映射)
比较均衡化图像和规定化图像,发现直方图规定化对直方图均衡化图像改进非常明显,图3.25©中图像的色调更均匀,并且噪声水平大幅降低,背景中的目标不像直方图均衡化图像中那么亮,但在图3.25©中是可见的,并且它的灰色调正好位于整个图像的内容中。右边的银碗和目标在直方图均衡化图像中看起来是饱和的(和周围环境没有区分度),但在图3.25©中的色调更自然,并出现了图3.24(b)中不可见的细节
局部直方图处理
迄今为止讨论的直方图处理方法都是全局性的,因为像素是由基于整个图像的灰度分布的变换函数修改的,这种全局性方法适合于整体增强,但当目的是增强图像中几个小区域的细节时,通常就会失败,这是因为在这些小区域中,像素的数量对计算全局变换的影响可以忽略。解决方法是设计基于像素邻域的灰度分布的变换函数。
这种基于像素邻域的灰度分布的变换函数的直方图处理技术适用于局部增强。这个过程是定义一个邻域,并将其中心在水平方向或垂直方向上从一个像素移动到另一个像素。在每个位置,计算邻域中的各点的直方图,得到直方图均衡化或规定化变换函数(局部直方图均衡及规定化,变换函数也是由像素邻域局部生成)。
这个关于像素邻域的变换函数用于映射邻域中心像素的灰度,然后将邻域的中心移到一个相邻像素位置,并重复这个过程。由于邻域中只有一行或一列(十字邻域)在这个邻域的1像素平移(平移一个像素单位)中发生变化,因此可用每个移动步骤中引入的新数据来更新在前一位置得到的直方图(每发生像素移动就更新直方图)。下面会用例子来解释如何更新。
这种方法在每次移动1像素位置时,都要重复计算邻域中所有像素的直方图。有时,降低计算量所用的另一种方法是利用非重叠区域(未发生像素移动的区域),但这种方法通常会产生我们不希望出现的“块状”效应。
“块状”效应
“块状”效应本质上是因为在图像的局部直方图处理时产生的处理后图像存在原图像中产生违和感,让人感觉这一块经过直方图处理的图像与原图像其他区域不搭,特别一些边缘的地方,如下图所示:

使用直方图统计量增强图像




说简单点就是利用灰度的均值和标准差来确定需要直方图处理的区域,首先利用均值来确定一个灰度差较大的像素,再者还需判断这个由均值确定出来的像素的标准差判断这个像素和周围像素之间的对比度,如果对比度在一个合适的区间,就判断这个像素是待处理像素,这样的局部增强相比局部直方图均衡化要精确得多。
空间滤波
空间滤波基础
“滤波”是指通过、修改或抑制图像的规定频率分量。
例如,通过低频的滤波器称为低通滤波器。低通滤波器的作用是通过模糊图像来平滑图像。使用空间滤波器可以直接对图像本身进行类似的平滑处理。
空间滤波通过把每个像素的值替换为该像素及其邻域的函数值来修改图像。
如果对图像像素执行的运算是线性的,那么称该滤波器为线性空间滤波器。否则,称该滤波器为非线性空间滤波器。
线性空间滤波的原理
线性空间滤波器在图像f和滤波器核w之间执行乘机之和运算。核是一个阵列,其大小定义了运算的邻域,其系数决定了该滤波器的性质。

上图说明了使用3x3核进行线性空间滤波的原理,在图像中的任何一点(x,y)处,滤波器的响应g(x,y)是核系数核核所覆盖图像像素的乘积之和。
坐标x和y变化时,核的中心逐个像素地移动,并在移动过程中生成滤波后的图像g(通常不覆盖原图像,而是新建图像)

空间相关与卷积
图3.28是空间相关的图形说明,式3.31式给出了其数学描述。
相关的运算过程如下:
在图像上移动核的中心,并且在每个位置计算乘积之和。
空间卷积的原理相同,只是把相关运算的核旋转180°。
因此当核的值关于其中心对称时,相关核卷积得到的结果相同。
在我们用滤波器核w去扫描图像f时,会发现w的一部分在f之外,发现求和在这个区域未定义,其中一个解决办法时在f的两侧补足够多的0,一般来说,如果核的大小为1xm,那么为了处理w相对于f的起始结构核结束结构,f的两侧都需要补(m-1)/2个0。
核w与一个(1个元素是1,其他元素是0)函数相关时,将得到w的一个副本,但这个副本旋转了180°。
这个函数,即一个元素时1,其余元素是0函数,称为离散单位冲激函数。核与离散单位冲激函数相关时,会在这个冲激的位置产生核的旋转版本。(这里“冲激的位置”可以理解为滤波器核中心与冲激函数匹配的位置,即冲激函数被扫描的位置)
卷积和相关唯一的不同是在执行移位/乘积之和前,核预先旋转了180°。
预先旋转核的作用是,现在在单位冲激的位置我们已有核的一个准确副本(卷积结果是原w的一个准确副本,即未旋转的核w)
事实上,线性系统理论的基础是将一个函数与一个冲激进行卷积,在冲激所在的位置产生这个函数的一个副本。(频率域滤波会广泛使用这个性质)
刚才讨论的一维概念很容易推广到图像,对于大小为mxn的核,我们在图像的顶部和底部分别至少补(m-1)/2行0,在图像的左侧和右侧分别至少补(n-1)/2列0。
这里补正的0的个数很好理解,零的个数由核的对半开的侧翼扁平的零个数决定,比如一维的核,去除中间数,侧翼的零的个数即需要补正的零的个数(核从中间数开始扫描),二维核同理。



由上图可以看到,函数与冲激的卷积把函数复制到了冲激所在的位置,若核的值关于核中心对称,则相关核卷积的结果相同
在二维情况下,旋转180°等效于核关于其一个轴翻转,然后关于另一个轴翻转,这里轴指通过核中心点的竖轴和横轴。
冲击这一概念是线性系统理论的基础,本书中的许多地方会用到它(待会解释一下),坐标(x0,y0)处的离散冲击强度(振幅)A定义为


这里对冲激的定义了解比较少,至于为何是在单位冲激的单位1中达到冲激振幅最大,这点我也还没搞清楚,权当了解。
可以将大小为mxn的核对大小为MXN的图像的线性空间滤波的空间相关可以表示为下面的公式:
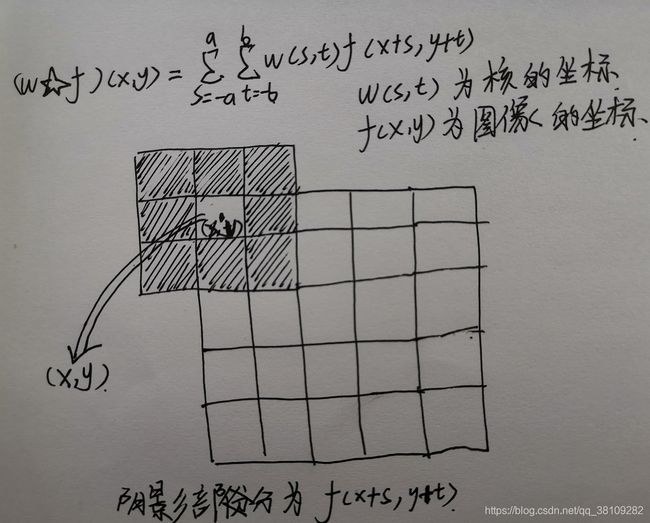
其中a=(m-1)/2,b=(n-1)/2,并且假设m核n是奇整数
类似地,大小为mxn的核w与图像f(x,y)的卷积(w★f)(x,y)定义为:

空间相关和空间卷积区别就是核的旋转,f函数中(x-s,y-t)相对(x+s,y+t)满足了关于核中心翻转180°的关系。

至于上述证明,可以通过数学上积分形式的卷积通过变量代换来证明。
可分离滤波器核
若二维函数G(x,y)可写为一维函数G1(x)和G2(x)的乘积,即G(x,y)=G1(x)G2(y),则它是可分离的。空间滤波器核是一个矩阵,而可分离核是一个能够表示为两个向量的外积的矩阵。
可证明:一个列向量和一个行向量的乘积,等于这两个向量的二维卷积
证明过程:
原书英文推理过程:

这里的最后一个等式中,rm应为rn,应该是作者打错。
关于上述英文解答的详细解答:
英文解答说明了,这是完全卷积,关于完全卷积
完全卷积的定义(二维完全卷积):
使得核w的每个元素(而非其中心元素)能够访问图像f中的每个像素。此时要求起始结构中的核的右下角与图像的原点重合,即以核的右下角与图像原点开始匹配遍历,类似地,要求结束结构中的核的左上角与图像的右下角重合。若核核图像的大小分别为mxn和MxN,则要再图像的顶部和底部分别补(m-1)行0(因为核的行为m,去除核中心行即m-1行),在图像的左侧核右侧分别补(n-1)列0。
在这些条件下,得到的完全卷积阵列的大小为SvxSh,
可以看上面的图3.30(e)和(h),其中
Sv=m+N-1
Sh=n+N-1
(完全相关的定义类似)
知道这点后,我们来看这个上面这个证明,并解释:

可分离核的重要性是卷积的结合律性质导致的计算优势。
如果有一个核w,它可分解为两个更简单的核并且满足w=w1★w2,那么根据卷积的交换律核结合律可以证明:
w★f = (w1★w2)★f = (w2★w1)★f = w2★(w1★f) = (w1★f)★w2
这个公式的实际意义指的是,一个可分离核与一幅图像的卷积,等于先用f与w1卷积,然后用w2对结果进行卷积。
这个公式的应用可以提高卷积的运算效率,具体请看:


这里将秩为1的矩阵分离成两个向量的操作,具体以下小核的习题:(以上方法步骤的第2个步骤,后面的印刷应该是“那一列和那一行”,因为步骤v=c,wT=r/E ,外积vwT=核,如果如文中所说c为那一行,则v为行向量,与外积定义矛盾。
PS:这里对秩为1的矩阵的分离对考研人应该非常熟悉,目测就能分离出来,但是当我们要用计算机去实现的时候,可能就有不同的感悟了,反而要我们用计算机的思维解析我们目测分离的逻辑,所以以下习题的练习还是有帮助的。
这里提到的关于圆对称下一节会有介绍
空间域滤波和频率域滤波的一些重要比较
空间域处理和频率域处理之间的联系纽带是傅里叶变换。我们用傅里叶变换从空间域进入频率域,用傅里叶反变换返回空间域。
这里的重点是与空间域和频率域有关的两个基本性质:
1.卷积是空间域滤波的基础,它等效于频率域中的乘法,反之亦然。
2.空间域中振幅为A的冲激,是频率域中值为A的一个常数,反之亦然。
在下一章节的频率域章节中,满足一些温和条件的函数(如图像)可以表示为不同频率和振幅的正弦波之和。因此,图像的外观依赖于其正弦分量的频率——改变这些分量的频率将改变图像的外观。这个强大概念成立的原因是,我们可以将某些频带与图像特征关联起来。例如,图像中灰度变化缓慢的区域(如图像中房间的墙壁)由低频正弦波表征。类似地。边缘和其他急剧的灰度过渡由高频正弦波表征。因此减少图像中的高频分量就会使图像变得模糊。
线性滤波就是找到合适的方法来修改图像的频率内容。
在空间域中,我们是通过卷积滤波来实现这一要求的。在频率域中,我们则是用乘法滤波器来实现这一要求的。后者是一种更直观的方法,它是在不具备关于频率域的一些基本知识的情况下,不可能真正理解空间滤波的原因之一。
这里要理解空间滤波还要掌握一些频率域的一些基本知识。


这里图(a)很直观的看出低通滤波器的作用,图(b)的观察需要频率域的基本知识,下一章节会仔细说明。
图(b)在高处的坐标达到峰值u0,类似在这个空间域达到冲激振幅最大,更多解释下一章会说明。

