【图像处理】道格拉斯-普克算法（曲线的折线段逼近）

目录

一、提要 

二、为什么要道格拉斯-普克算法

三、算法描述

四、代码实现

4.1 Python代码1

4.2 python代码2

五、结论

---

一、提要 

        描述一个物体外轮廓，如何用的描述点少，而且特征尽量保留？这就是 拉默-道格拉斯-普克算法。

        拉默-道格拉斯-普克算法（英语：Ramer–Douglas–Peucker algorithm）是Urs Ramer在1972年时候，在他的论文《平面曲线的多边形逼近的迭代过程》中提出，又称道格拉斯-普克算法（英语：Douglas–Peucker algorithm）和迭代端点拟合算法（英语：iterative end-point fit algorithm），是一种将线段组成的曲线降采样为点数较少的类似曲线的算法。它是最早成功地用于制图综合的算法之一。   

二、为什么要道格拉斯-普克算法

        在开发路径跟踪应用程序时候，需要使用某种折线简化算法，比如，路径是一个圆周，那么用圆周上的点表达路径，远不如用等边多边形表示更加经济（图1）。我们需要该算法来减少要保存到数据库中的路线点（纬度、经度）的数量。显然，用12个边的多边形近似为圆的路径，数据规模可以大幅度降低。

图1 用多边形近似表示曲线圆周

        至于路径复杂的时候，这种线段拟合更有必要。如下图：找出曲线最关键的少量点连成的折线表示整条连续曲线，且不会造成太多误差。

图2 用点序表示的函数曲线，还可以更加简化，形状未变

        因此，道格拉斯-普克算法的目的是：给定一条由线段构成的曲线（在某些情况下也称为折线），找到一条点数较少的相似曲线。该算法根据原曲线与简化曲线之间的最大距离（即曲线之间的豪斯多夫距离）来定义 "不相似"程度。简化曲线由定义原始曲线中点的子集组成。

三、算法描述

      1973 年，David H. Douglas 和 Thomas K. Peucker 发表了一篇题为“减少表示数字化线或其漫画所需的点数的算法”的论文（Douglas & Peucker, 1973）。他们在其中介绍了两种算法。其中之一已被广泛实施，通常称为 Douglas Peucker 算法。该算法的目的是生成一条简化的折线，其点数少于原始折线，但仍保持原始的特征/形状。

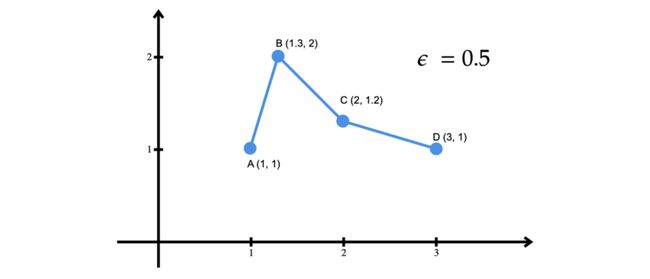
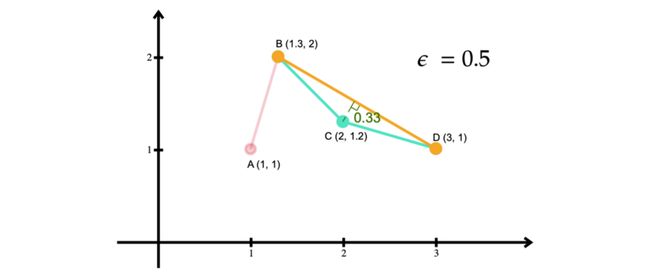
        要了解该算法的工作原理，我们可以逐步了解它是如何在图3中的四点折线上运行的。

图3 假想的原始的多边形状图

Step 1

图4: 边界点连线是AD，求非边界点到AD的距离

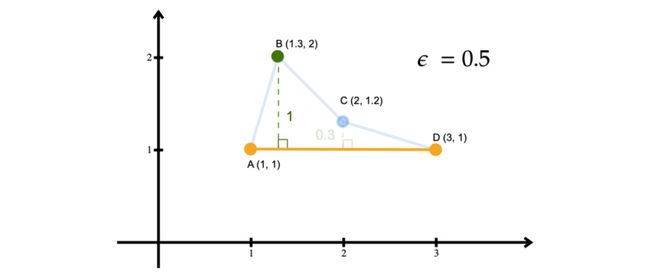
        该算法首先确定折线的起点和终点。在他们的论文中，Douglas & Peucker (1972) 将这两个点分别称为锚点和浮点。在我们的示例中，这些点是 A（开始）和 D（结束）。对于折线中既不是起点也不是终点的待定点（B 和 C），它计算从该点到起点和终点形成的线的“垂直距离”。这给了我们 d(B, AD) = 1 和 d(C, AD) = 0.3。

Step 2

图5 B是离开AD线段最远的点，d(B,AD)>0.5

        然后算法选择最远的点。在我们的示例中，该点是 B。我们将此点称为 MAX。然后它将 d(B, AD) 与 epsilon (ε) 值（在我们的示例中为 0.5）进行比较。由于 d(B, AD) > ε，算法将折线分成两个子段。一段由 MAX 左侧的所有点（A 和 B）组成，另一段由 MAX 右侧的所有点（B、C 和 D）组成。

图6 最远点B原始问题分成两段，AB段和BD段，递归处理

Step 3

图7 因为AB线段中间无点，因此，AB保留，处理结束。

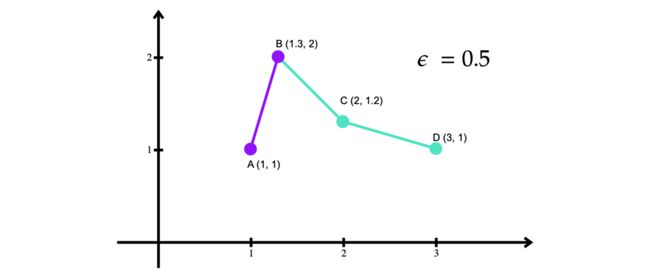
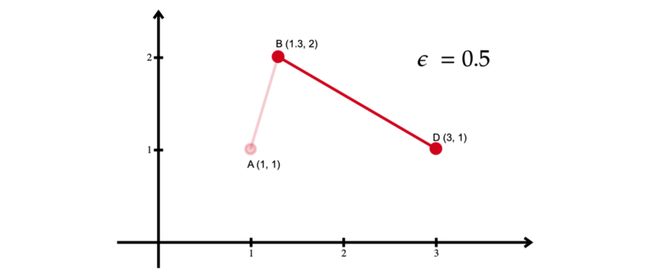
        然后算法在第一段再次执行步骤 1。它将起点和终点分别标识为 A 和 B。但是，与之前的迭代不同，此段中只有两个点。在这种情况下，该算法不能进一步减少点的数量，因为直线是任何折线的最简单近似。因此，保留 A 和 B。

图8 第一段曲线已经确定为AB，标红

Step 4

图9 针对第二段折线BD，处理其它待定点（C）

        类似地，对于第二段，算法执行步骤 1 以将 B 和 D 标识为起点和终点，并计算所有剩余点（在我们的示例中只有 C）与 B 和 D 形成的线之间的垂直距离。

图10 检查C点到BD线段距离，发现d(C,BD)<0.5

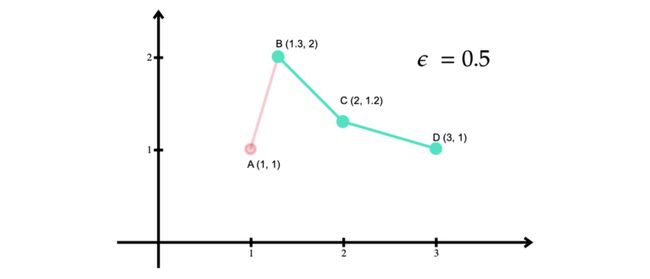
        由于除了 B 和 D 之外唯一剩下的点是 C，因此它是距离最远的点。因此，该算法将 d(C, AB) 与 ε 进行比较。与第一次迭代不同，d(C, AB) < ε。因此，可以删除点 C，只保留该段的 B 和 D。

图11 在BC折线段处理中，删除C点后，变为BC线段选中

Step 5

图13 最后的处理结果，是ABD折线

        在完成第一段和第二段的所有迭代后，该算法将所有结果组合在一起以创建原始折线的简化版本。

四、代码实现

        下面的代码对 Douglas Peucker 算法最简单形式的实现。此实现基于此 Wikipedia 页面提供的关于此主题的伪代码。我确信那里有更有效的实施。相信下面的代码足以理解算法的底层思想。

4.1 Python代码1

import matplotlib.animation as animation
import matplotlib.pyplot as plt
import numpy as np


def rdp(points, epsilon):
    # get the start and end points
    start = np.tile(np.expand_dims(points[0], axis=0), (points.shape[0], 1))
    end = np.tile(np.expand_dims(points[-1], axis=0), (points.shape[0], 1))

    # find distance from other_points to line formed by start and end
    dist_point_to_line = np.abs(np.cross(end - start, points - start, axis=-1)) / np.linalg.norm(end - start, axis=-1)
    # get the index of the points with the largest distance
    max_idx = np.argmax(dist_point_to_line)
    max_value = dist_point_to_line[max_idx]

    result = []
    if max_value > epsilon:
        partial_results_left = rdp(points[:max_idx+1], epsilon)
        result += [list(i) for i in partial_results_left if list(i) not in result]
        partial_results_right = rdp(points[max_idx:], epsilon)
        result += [list(i) for i in partial_results_right if list(i) not in result]
    else:
        result += [points[0], points[-1]]

    return result


if __name__ == "__main__":
    min_x = 0
    max_x = 5

    xs = np.linspace(min_x, max_x, num=200)
    ys = np.exp(-xs) * np.cos(2 * np.pi * xs)
    sample_points = np.concatenate([
        np.expand_dims(xs, axis=-1),
        np.expand_dims(ys, axis=-1)
    ], axis=-1)

    # First set up the figure, the axis, and the plot element we want to animate
    fig = plt.figure()
    ax = plt.axes(xlim=(min_x, max_x), ylim=(-1, 1))
    plt.xlabel("x")
    plt.ylabel("y")
    text_values = ax.text(
        0.70,
        0.15,
        "",
        transform=ax.transAxes,
        fontsize=12,
        verticalalignment='top',
        bbox=dict(boxstyle='round',
                  facecolor='wheat',
                  alpha=0.2)
    )
    original_line, = ax.plot(xs, ys, lw=2, label=r"$y = e^{-x}cos(2 \pi x)$")
    simplified_line, = ax.plot([], [], lw=2, label="simplified", marker='o', color='r')

    # initialization function: plot the background of each frame
    def init():
        simplified_line.set_data(xs, ys)
        return original_line, simplified_line, text_values

    # animation function.  This is called sequentially
    def animate(i):
        epsilon = 0 + (i * 0.1)
        simplified = np.array(rdp(sample_points, epsilon))
        print(f"i: {i}, episilon: {'%.1f' % epsilon}, n: {simplified.shape[0]}")
        simplified_line.set_data(simplified[:, 0], simplified[:, 1])
        text_values.set_text(fr"$\epsilon$: {'%.1f' % epsilon}, $n$: {simplified.shape[0]}")
        return original_line, simplified_line, text_values

    # call the animator.  blit=True means only re-draw the parts that have changed.
    anim = animation.FuncAnimation(
        fig,
        animate,
        init_func=init,
        frames=21,
        interval=1000,
        repeat=True
    )
    plt.legend()
    plt.show()

 参考结果：

4.2 python代码2

股市曲线的简化 参考代码(仅供参考)。

import numpy as np
import matplotlib.pyplot as plt

import yfinance as yf
from rdp import rdp

stock = "AMZN"
start = "2020-11-01"

dataframe = yf.download(stock, start=start)

nfx, nfy = [], []
for index, row in dataframe.iterrows():
    nfx.append(index.timestamp())
    nfy.append(row["Close"])

# print(nfx)
points = np.column_stack([nfx, nfy])
print("points.shape:", points.shape)
points_after_rdp = rdp(points, epsilon=80)

# Graph
plt.plot(points_after_rdp[:, 0], points_after_rdp[:, 1], color="red", label="after RDP")
plt.plot(
    points[:, 0], points[:, 1], color="black", label="before", alpha=0.7, linewidth=1
)
plt.xlabel("time (s)")
plt.ylabel("Close")
plt.legend()
plt.show()

 结果展示

五、结论

        在该文中，我们学习了一种有用且简单的算法，用于减少折线图中的点数。除了这篇文章的示例之外，该算法还可以应用于更多现实世界的应用，包括加速地图渲染、改善物联网设备之间的通信等。希望这篇文章能帮助你理解算法并将其应用到更多有用的应用程序中。