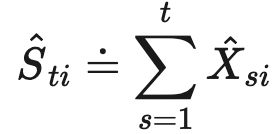【Bandit Algorithms学习笔记】EXP3算法理论证明
本系列记录了笔者学习bandit algorithms的笔记,包含相关算法的介绍和理论推导。
【Bandit Algorithms学习笔记】Explore-Then-Commit算法
【Bandit Algorithms学习笔记】UCB算法的理论证明
【Bandit Algorithms学习笔记】EXP3算法理论证明
文章目录
-
- 对抗式赌博机
- Exp3算法
-
- 流程
- 奖励的估计值
-
- 奖励估计值的方差
- 概率计算
- EXP3遗憾计算
-
- 推论1
- 证明
- 课后思考题
- 总结
- 参考资料
对抗式赌博机
在bandit问题中我们更应该关心随机bandit模型是不是能用而不是模型正不正确。模型正确与否通常用预测结果表示,模型是否好用通常用模型预测结果的准确率表示。
对抗式赌博机
对抗式赌博机不去假设奖励是如何生成的,我们通常叫对抗式赌博机的环境为对手(adversary)。目标是用来表述一个策略是否能够很好地和最优的动作对抗。
你可以想象一下和朋友在玩这样一个游戏,游戏流程如下:
- 你告诉你的朋友你要选择的动作,动作有1或2.
- 你的朋友秘密选择奖励x1 {0,1} 和x2 {0,1}
- 你使用你的策略去选择动作A1或A2 ,然后得到奖励x_A
- 遗憾就等于 R = m a x { x 1 , x 2 } − x A R = max \{x_1, x_2\} -x_A R=max{x1,x2}−xA
因此我们可以看到,adversarial bandit和stochastic bandit的区别是,前者的奖励是对手随机给出的(你可以想象一个赌场中,赌博机是能被人为操控的),而后者的奖励概率在我们之前讨论过的章节中是确定的(也就是每个bandit以概率 P i P_i Pi吐钱或者不吐钱)。
对抗式赌博机问题和随机赌博机问题相似,都有许多不同的推论,在下面的内容中我们将开始讨论。
Exp3算法
流程
关于adversarial bandit最常见的算法就是EXP3,EXP3的计算流程如下:
- 根据先前计算得到的 P t i P_{ti} Pti采样的得到 A t A_t At
- 执行动作得到奖励,根据奖励的观测值 X t i X_{ti} Xti 估计每个动作的奖励估计值
- 用奖励的估计值更新概率 P t i P_{ti} Pti
第一轮,初始化每个动作被执行的概率为1/K。
奖励的估计值
所有对抗式赌博机算法的关键都是一套机制,采用这种机制去估计没有玩过的赌博机臂的奖励。 P t P_t Pt是第t轮动作的条件概率。对于i属于[k], P t i P_{ti} Pti的条件概率是(执行A1,得到奖励X1,执行A2,得到奖励X2,一直到执行A_t-1得到奖励X_t-1的条件下)执行动作A_i的概率。
我们定义 x t i x_{ti} xti的估计值为 :

X t i X_{ti} Xti的条件期望满足, E t − 1 [ X t i ] = x t i E_{t-1}[X_{ti}] = x_{ti} Et−1[Xti]=xti,意味着 X t i X_{ti} Xti在t-1轮历史观测的条件下是 x t i x_{ti} xti的无偏估计。我们设定 A t i = I { A t = i } A_{ti} = I \{A_t = i\} Ati=I{At=i}因此有 X t A t i = x t i A t i X_tA_{ti} = x_{ti}A_{ti} XtAti=xtiAti,并且 E t [ A t i ] = P t i E_{t}[A_{ti}] = P_{ti} Et[Ati]=Pti,并且因为 P t i P_{ti} Pti是 σ ( A 1 , X 1 , . . . , A t − 1 , X t − 1 ) \sigma(A_1, X_1, ..., A_{t-1}, X_{t-1}) σ(A1,X1,...,At−1,Xt−1)可测的。因此有:

奖励估计值的方差
我们还需要计算奖励估计值的方差,因为如果奖励估计值的方差很小,证明我们的算法就越稳定,相反如果奖励估计值的方差太大,或许这个算法就不值得被使用。因此,我们需要考虑奖励估计值 X t i X_{ti} Xti的方差 V t [ X t i ] V_{t}[X_{ti}] Vt[Xti]。
根据条件方差的定义式

结合
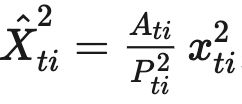
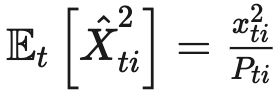
我们容易得到:

但是,观察这个式子我们能够看出一个问题:
概率越小的动作,方差越大。
因此,这样设定估计值对概率小的动作非常不友好,为了解决这个问题,设定另外一个估计值:
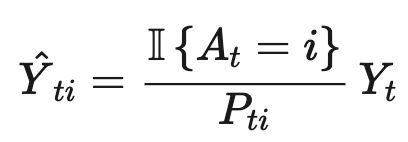
其中, y t i = 1 − x t i , Y t = 1 − X t y_{ti} = 1- x_{ti}, Y_{t} = 1- X_{t} yti=1−xti,Yt=1−Xt。如此一来,根据方差的性质我们能够得到:前一种估计方式和后一种估计方式的方差是相等的,即:

前者估计值的范围是0到正无穷,后者的范围是负无穷到1,所以后者估计值的方差较小,对“好动作” 的估计值会更加精准。
概率计算
对于前t轮奖励和越高的动作,我们自然是希望执行这个动作的概率越高,这样便于指导我们在接下来的几轮中获得更多的奖励。我们需要将奖励和映射为概率,这样便于我们选取动作:

你可以理解 η \eta η为学习率,值越大,越倾向于选择奖励高的动作。
为了便于计算,我们常常采用增量形式的概率计算:

虽然这样的计算方式对于较大的n和K而言会使得数据不置信。
EXP3遗憾计算
上述的前置知识介绍完之后,我们进入EXP3算法的遗憾期望计算。
推论1
对于上述adversarial bandit问题,其遗憾满足下面式子:

证明
根据遗憾的定义式: R n = Σ t = 1 n X t i − E [ Σ t = 1 n X t ] Rn = \Sigma_{t=1}^{n} X_{ti} - E[\Sigma_{t=1}^nX_t] Rn=Σt=1nXti−E[Σt=1nXt],因为奖励的估计值是无偏的,因此, E [ S n i ] = Σ t = 1 n x t i E[S_{ni}] = \Sigma_{t=1}^nx_{ti} E[Sni]=Σt=1nxti,并且 E [ X t ] = Σ i P t i x t i = Σ i P t i E [ X t i ] E[X_t] = \Sigma_i P_{ti} x_{ti} = \Sigma_iP_{ti}E[X_{ti}] E[Xt]=ΣiPtixti=ΣiPtiE[Xti],因此 E [ Σ t = 1 n X t ] = Σ t , i P t , i X t , i E[\Sigma_{t=1}^nX_t] = \Sigma_{t,i}P_{t,i}X_{t,i} E[Σt=1nXt]=Σt,iPt,iXt,i因此我们定义 S n Sn Sn拔等于 Σ t , i P t , i X t , i \Sigma_{t,i}P_{t,i}X_{t,i} Σt,iPt,iXt,i,因此就有遗憾改写为:

为了便于下文推导,我们将上式指数化,得到 e x p ( η S n i ) exp(\eta S_{ni}) exp(ηSni),我们还定义:

因此有 W 0 = K , S 0 i = 0 W_0 = K, S0i = 0 W0=K,S0i=0,那么便有以下式子:
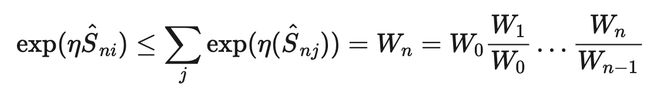
根据上式规律,我们需要找出Wt / Wt-1,
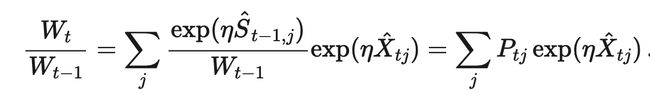
观察上式最右边的指数形式,我们根据不等式 e x ≤ x 2 + x + 1 , x < 1 e^x \leq x^2 + x +1,x <1 ex≤x2+x+1,x<1和不等式 e x ≥ x + 1 e^x \geq x +1 ex≥x+1,得到:
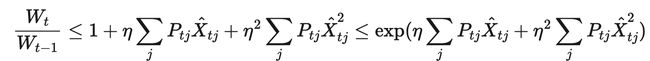
综上变形得到:

上式取对数后变形得到:
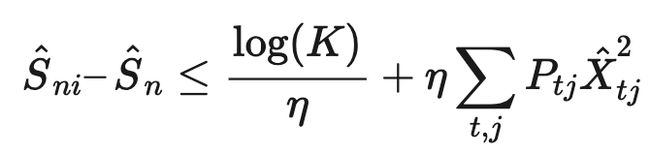
我们可以找到上式最右边一项的上界为:

最终放缩得到:
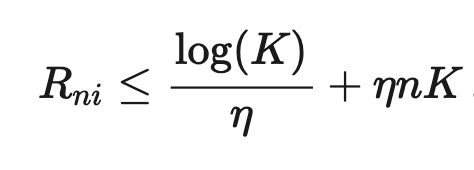
根据高中所学的对勾函数的性质,我们容易得到遗憾上界为:

证明完毕。
课后思考题
我们之前的证明是采用X估计值,也就是第一种估计值证明遗憾的期望,小伙伴们可以试着用Y的估计值证明一下遗憾的期望,看看能得出什么结论吧~
总结
本文介绍了对抗式赌博机adversarial bandit问题以及解决此问题常见的exp3算法,并对exp3算法的遗憾上界做出了证明。
参考资料
book
https://banditalgs.com/2016/10/01/adversarial-bandits/#mjx-eqn-equnbiasedness
https://www.zhihu.com/question/53381093?sort=created