Matlab代码实现强化学习(Reinforcement Learning) 二维迷宫探索——Q-learning与SARSA对比

前一篇文章https://blog.csdn.net/qq_35694280/article/details/106446214介绍了使用Matlab代码如何利用Q-learning或者SARSA在一维空间实现探索，并且训练机器如何自动达到目标。这篇文章在此基础上将一维空间延伸至二维空间，将算法应用到二维空间的探索与训练上，最终实现规划的目标。这篇文章也承接上一篇，通过在二维环境中Q-learning与SARSA的表现来展示二者的区别。

一、问题描述

本文针对的二维环境如图所示

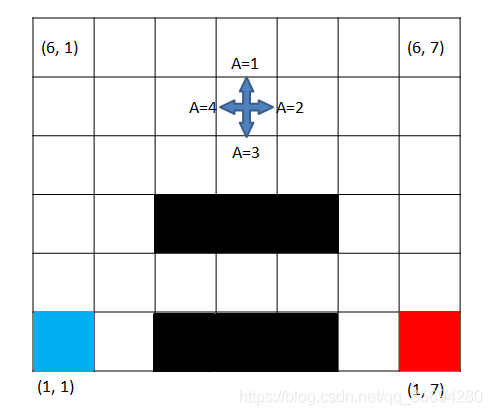
是一个二维网格模型，我们将其描述为迷宫，因为在此基础上可以延伸至任何一个二维网格模型。网格一共分为6行7列共$6\times 7$个网格，其中左下角蓝色格子为探索的起点，红色格子为我们的目的地，即希望机器能够最终到达这个出口，黑色的格子表示陷阱，只要落入黑色格子则本轮结束以失败告终。在每个格子中机器可以朝上、右、下、左四个方向移动，对应的动作分别为$A=1,2,3,4$，在边缘的格子则只能朝相邻的格子移动，不可以超出边界。

二、模型定义

为了将环境描述为程序易于表达的形式，我们将每个格子进行编号，从1至42，第一行从左至右分别是$1,2,3,4,5,6,7$，第二行从左至右则分别是$8,9,10,11,12,13,14$，以此类推，将所有格子进行编号，这个编号也方便与每个格子对应的坐标进行换算。在中间的格子有四个动作选择，可以往上、下、左、右任意一个方向移动，在边缘的格子则只能选择三个动作，在角落的格子则只有两个选择。

为了使机器能够自主学习，我们需要对环境的reward进行定义，暂时将出口处的reward设置为1，陷阱处的reward则设置为-1，其他任何格子reward为0。至此模型的定义完成。

三、算法

本文所用的算法就是最基础的Q-learning与SARSA算法，相关的理论知识可以参考别的教程，这里不再赘述。如果感兴趣可以参考上一篇文章，将RL应用在一维环境中，之后再来读这篇文章可能会更加容易理解，因为两者的算法基本相同，不同之处只在于环境的改变，以及状态空间维数变大，求解更加费时。话不多说，直接上代码。

四、代码

与前文相同，本文代码依然是分为三块，分别是主程序$\text{Maze\_main}$以及动作函数$\text{choose\_action}$和环境函数$\text{get\_env\_feedback}$.其中主程序代码如下

clear; clc; close all;
% RL implementation on a finite-state maze exploration
% 设置参数：状态量个数，动作的个数，最大循环数
global Maze_row Maze_col epsilon goal_num;
Maze_row = 6; Maze_col = 7; epsilon = 0.9;
state_num = Maze_row*Maze_col; 
action_num = 4;
episode_max = 20000;
% 这两个参数很重要，适当的调节可以更好地学习最优解
Gama = 0.8; % discout factor
Alpha = 0.2; % 学习速率
% 初始化Q值表
Q_table = zeros(state_num, action_num);
% 目标点的坐标，以及位置编号；起始点的位置及编号
goal = [1, 7]; goal_num = (goal(1)-1)*Maze_col+goal(2);
start = [1, 1]; start_num = (start(1)-1)*Maze_col+start(2);

for i=1:episode_max
    % 每次训练的初始化
    step_counter = 0;
    S = start_num;
    is_terminal = false;
    choices = Q_table(S, :);
    action = [];
%     A = choose_action(S, choices); % SARSA对初始状态采取的动作的初始化
    while ~is_terminal
        % 选择动作，更新状态，更新Q表
%         action = [action A]; % SARSA动作收集
        step_counter = step_counter + 1;
        choices = Q_table(S, :);
        A = choose_action(S, choices); % Q-learning采用的动作
        [S_, R, flag] = get_env_feedback(S, A);
%         A_ = choose_action(S_, choices); % SARSA中对下一状态的动作选择
        Q_predict = Q_table(S, A);
        % 根据下一步是否是终点来更新flag参数以及Q值
        if S_ ~= goal_num && flag == 0
            % 当下的reward加上下一步的discounted Q-value
            Q_target = R + Gama * max(Q_table(S_, :)); % Q-learning更新
%             Q_target = R + Gama * Q_table(S_, A_); % SARSA更新，下一状态采用A_
        elseif flag == 1 % 落入陷阱，直接终止
            Q_target = R;
            Q_table(S, A) = Q_table(S, A) + Alpha * (Q_target - Q_predict);
            break;
        else
            % 如果是终点就没有下一步，直接赋值
            Q_target = R;
            is_terminal = true;
        end
        Q_table(S, A) = Q_table(S, A) + Alpha * (Q_target - Q_predict);
        S = S_; % 更新状态量
%         A=A_; % 更新动作值，SARSA选择的下一动作-说到做到
        if step_counter > 10000
            break
        end
%         action = [action A]; % Q-learning动作收集
    end
    if S==goal_num
        fprintf('%d: Succeed! total step: %d\n', i, step_counter);
%         if step_counter<12
%             disp(action);
%         end
    elseif flag == 1
        fprintf('%d: Danger, failed! total step: %d\n', i, step_counter);
    else
        fprintf('Emergency break\n');
    end
end
Q_table

注意，将注释中含有Q-learning的代码行注释掉，并且将注释中含有SARSA的代码去注释，则可以实现两种算法的切换，反之亦然。主程序部分与一维情况下的代码差别不大，主要是环境函数与动作函数有所不同，分别如下

function A = choose_action( S, choices )
% 选择动作1,2,3,4，分别对应上下左右的动作
%   greedy policy
global Maze_row Maze_col epsilon;
% 找到S对应的坐标
col = mod(S, Maze_col); % 列
if col == 0
    col = Maze_col;
end
row = ceil(S/Maze_col); % 行

a = rand;

if col>1 && col<Maze_col && row>1 && row<Maze_row
    if a>epsilon || ~any(choices)% 在初始状态都为0的时候保证随机选取，而不是总选择第一个
        A = ceil(4*rand);
        return
    else
        [maximum ,A] = max(choices); 
        return
    end
elseif row == 1
    if col == 1  % 在坐标(1,1), A=1 or 2
        S_choices = [choices(1), choices(2)];
        if a>epsilon || ~any(S_choices)
            A = ceil(2*rand);
            return
        else
            [maximum ,A] = max(S_choices); 
            return
        end
    elseif col == Maze_col % position(1,7), A = 1 or 4
        S_choices = [choices(1), choices(4)];
        if a>epsilon || ~any(S_choices)
            A = ceil(2*rand);
        else
            [maximum ,A] = max(S_choices); 
        end
        if A == 2
            A = 4;
            return
        else
            return
        end
    else  % position between from (1,1) to (1,7) , action 1, 2, or 4
        S_choices = [choices(1), choices(2), choices(4)];
        if a>epsilon || ~any(S_choices)
            A = ceil(3*rand);
        else
            [maximum ,A] = max(S_choices); 
        end
        if A == 3
            A = 4;
            return
        else
            return
        end
        
    end
elseif row == Maze_row
    if col == 1  % 在坐标(6,1), A=2 or 3
        S_choices = [choices(2), choices(3)];
        if a>epsilon || ~any(S_choices)
            A = ceil(2*rand);
            A = A+1;
            return
        else
            [maximum ,A] = max(S_choices);
            A = A+1;
            return
        end
    elseif col == Maze_col % position(6,7), A = 3 or 4
        S_choices = [choices(3), choices(4)];
        if a>epsilon || ~any(S_choices)
            A = ceil(2*rand);
            A = A+2;
            return
        else
            [maximum ,A] = max(S_choices); 
            A = A+2;
            return
        end
    else  % position between from (6,1) to (6,7) , action 2, 3, or 4
        S_choices = [choices(2), choices(3), choices(4)];
        if a>epsilon || ~any(S_choices)
            A = ceil(3*rand);
            A = A+1;
            return
        else
            [maximum ,A] = max(S_choices); 
            A = A+1;
            return
        end
    end
elseif col == 1  % 不包括顶点 A=1,2 or 3
    S_choices = [choices(1), choices(2), choices(3)];
        if a>epsilon || ~any(S_choices)
            A = ceil(3*rand);
            return
        else
            [maximum ,A] = max(S_choices); 
            return
        end
    
elseif col == Maze_col % 不包括顶点 A=1,3 or 4
    S_choices = [choices(1), choices(3), choices(4)];
        if a>epsilon || ~any(S_choices)
            A = ceil(3*rand);
        else
            [maximum ,A] = max(S_choices); 
        end
        if A == 1
            return
        else 
            A = A+1;
            return
        end
end
end

动作函数这里比较麻烦，因为针对每一个格子可选择的动作不同，所以有很多的判断语句，并且由于使用了$ϵ\text{-greedy}$的探索方式，每一种情况下都要比较随机数进行概率判断。相比之下环境函数则比较简单，只需要在坐标的基础上直接加减即可。

function [S_, R, flag] = get_env_feedback(S, A)
%GET_ENV_FEEDBACK 此处显示有关此函数的摘要
%   此处显示详细说明
global Maze_row Maze_col goal_num
trap = [3,4,5,17,18,19];
% 找到S对应的坐标
col = mod(S, Maze_col); % 列
if col == 0
    col = Maze_col;
end
row = ceil(S/Maze_col); % 行

flag = 0;
if A == 1  % 向上移动
   row = row+1;
elseif A == 2 % 向右移动
    col = col+1;
elseif A == 3 % 向下移动
    row = row-1;
elseif A == 4 % 向左移动
    col = col-1;
end
    
S_ = Maze_col*(row-1) + col;

if S_ == goal_num
    R = 1;
elseif ismember(S_, trap)
    R = -1;
    flag = 1;
else
    R=0;
end
end

注意在环境函数与动作函数中都需要先将格子的编号转换为坐标，然后再进行运算。代码全部完成。

五、仿真结果

首先是Q-learning的结果

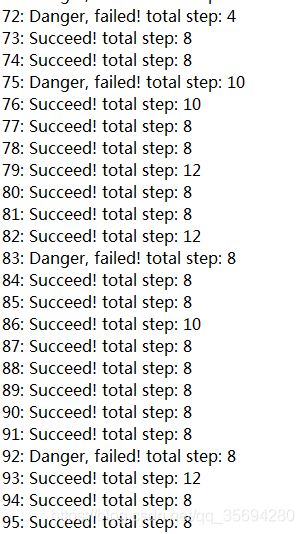
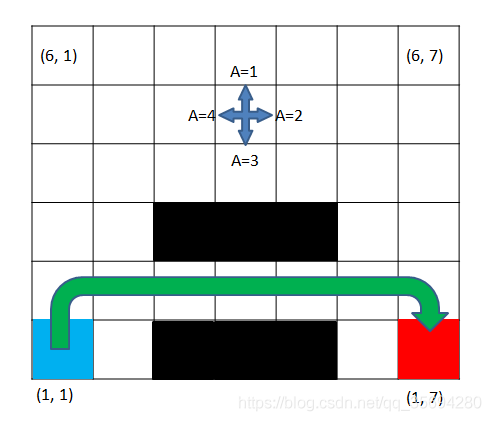
大概在100次训练之后基本上就已经收敛到最优，通过分析Q-table可以判断Q-learning选择的最优路径为

相比之下，SARSA的训练结果为

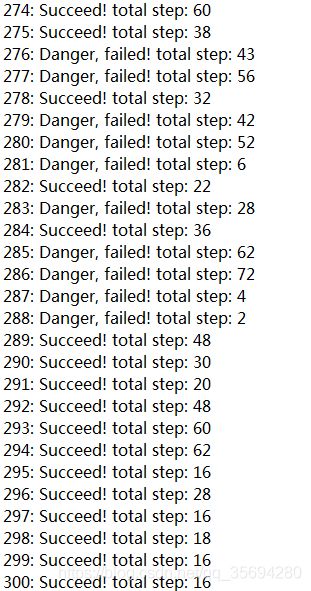
可以发现SARSA的收敛更慢，而且达到的最优解只不过是次优。另外，在仿真的过程中，SARSA很容易训练失败，无法达到目标。因为一旦落入陷阱，机器就会“一朝被蛇咬，十年怕井绳”，从此止步不前，特别是在环境比较恶劣的情况下，比如从$(1,2)$到$(1,6)$全部为陷阱时。但是同样情况下Q-learning更加稳定。SARSA的最优路径为：

对比发现，Q-learning算法相比SARSA更加大胆，用于尝试，SARSA则显得比较谨慎，故而二者的区别在这里就更加明显地体现出来了。值得一提的是，学习速率$\alpha$与discount factor $\gamma$对于学习的结果影响较大，当设置$\alpha =0.1,\gamma =0.9$时，机器比较不容易学习到最优解，当设置为$\alpha =0.2,\gamma =0.8$之后，情况则有所改善，故参数的设置对于学习的影响不能忽略，大家在实际应用的过程中也是要注意这一点，适当地调节参数改善学习。最后，本文提供了较为基础的模型，感兴趣的朋友可以将二维环境做任意的改变，发掘更多有意思的现象。另外如果有什么问题欢迎交流讨论，觉得这篇文章有用的话不要忘了点个赞~