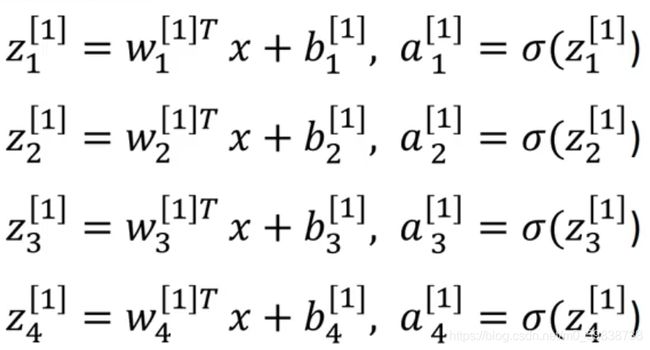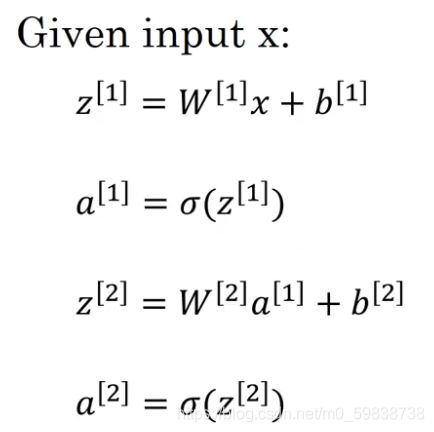吴恩达神经网络和深度学习-week3-浅层神经网络的要点记录
本文所有截图来自于吴恩达深度学习课视频课程。
1、神经网络的表示
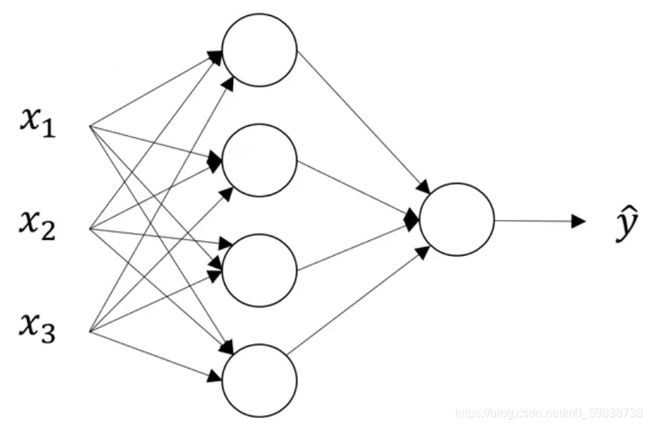
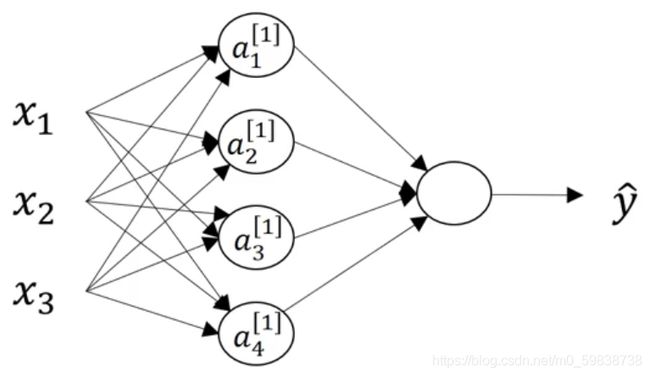
上图是一个双层神经网络的例子,包括一层隐藏层和一层输出层,输入层不算做标准层,有时也将输入层成为第0层。
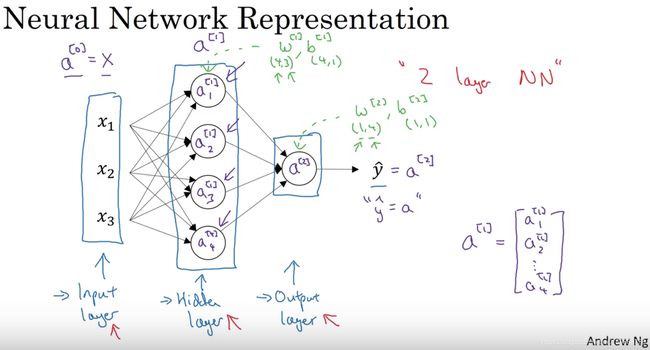
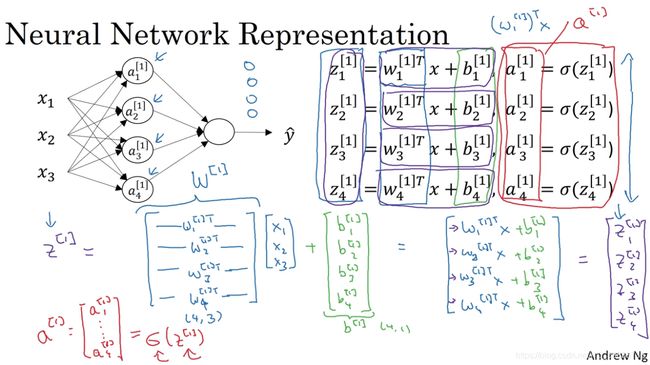
下图详细描述了神经网络的主要构成:
最左边是输入层,输入层的x1, x2, x3是样本x的三个特征值(上图只是一个样本的例子),例如:一张图片中,使用R、G、B三个通道的值来表示一个像素点,那么x1, x2, x3就对应这三个通道的值。输入层的激活值写为a^[0],即x=a^[0].
中间四个神经元是隐藏层,上图只有一层隐藏层,产生的激活值写为a^[1],一个神经元有一个实数的激活值,因此a^[1]是一个四维列向量,因为该隐藏层有四个单元。隐藏层之所以叫隐藏层,是因为我们在训练样本中,能观察到输入层和输出层的值,但是无法得知隐藏层中的值。
右边的一个神经元是输出层,产生的激活值是一个实数,写作a^[2],y^hat = a^[2]
隐藏层和输出层是带参数的:
隐藏层参数:W^[1], b^[1],其中,W^[1]的形状为 (4, 3),b^[1]的形状为 (4, 1)
输出层参数:W^[2], b^[2],其中,W^[2]的形状为 (1, 4),b^[1]的形状为 (1, 1)
如何判断w^[i]的形状:行数为第i层的神经单元数量,列数为第i-1层神经单元数量,如果第i-1层为输入层,则w^[i]的列数为特征数量。
2、神经网络的输出
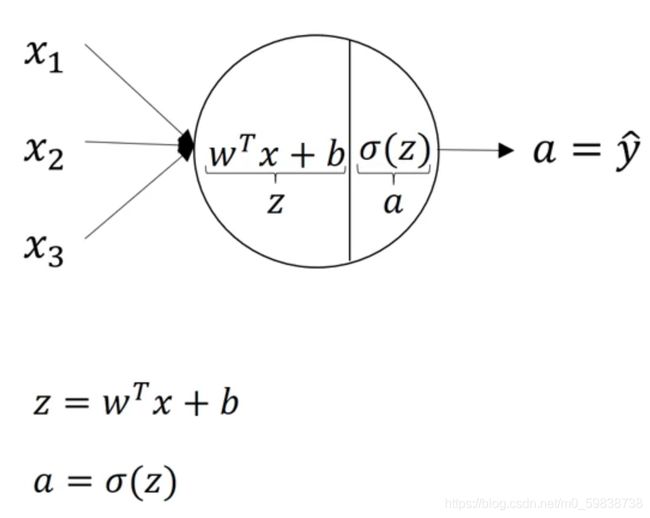
每个神经单元包括下图所示的两步计算(以sigmoid函数为例):产生z和a
在参数w和b的控制下,z和a的计算如下:
符号说明:
方括号上标 [i] 表示神经网络的第i层;
数字下标i表示当前层从上往下数的第i个神经单元,i=1,2,...
以上四个等式中各个参数的形状:
w^[1]_i: (3, 1)
b^[1]_i: (1, 1),为实数
z^[1]_i: (1, 1),为实数
a^[1]_i: (1, 1),为-1到1的实数
为避免低效的for循环,需要将以上四行等式向量化。
3、正向传播的向量化过程:当输入是一个样本时
进行向量化的一条经验准则:将同一层中的不同单元的同符号参数进行纵向堆叠,如下图:
输入为单个样本x(x有3个特征:x1, x1, x3)
向量化后的计算只需要如下四行(注意W是将以前的w进行转置后才进行的纵向堆叠,如上图蓝色手写部分):
各参数的形状手写如下(一定要弄清楚每一个参数的形状!):
4、正向传播的向量化过程:当输入是一组样本时
用圆括号上标 (i) 表示第i个样本
堆叠输入样本x:将不同样本以列向量堆叠起来,形成输入矩阵X,X的每一列表示一个样本的所有特征值,X的行数(n_x)为特征数量,列数(m)为样本数量;
堆叠z:将某一层不同样本计算得到的不同z以列向量堆叠起来,形成Z,Z的每一列表示一个样本计算得到的z,z是一个列向量,维度等于它所在层的神经单元数量;
堆叠a:将某一层通过不同z计算得到的不同a以列向量堆叠起来,形成A,A的每一列表示一个样本计算得到的a,a是z经过sigmoid计算得到的,因此a与z形状相同;
参数W和b是只和当前层相关,它们的形状和样本数目无关,换句话说,W和b的形状不会因为样本数目的不同而发生变化。
按以上规则排列后,矩阵的横向索引对应了不同的训练样本,矩阵的纵向索引对应了当前层的神经单元序号。因此,横向扫描整个样本空间,纵向扫描所有隐藏单元。
例如:矩阵A^[1]的左上角数值对应的是第一个训练样本上第一个隐藏单元(最上面那个单元)的激活函数,它下面那个值对应第一个训练样本上第二个隐藏单元的激活函数。以此类推,矩阵A^[1]的右下角数值对应的是最后一个训练样本上最后一个隐藏单元(最下面那个单元)的激活函数。
向量化结果:
单隐层神经网络中各个参数的形状如下:
| 参数 | 形状 | 变量说明 | 上图例子的值 |
|---|---|---|---|
| X | (n0, m) | n0是输入特征数量(也可写作nx),m是样本数量 | (3,m) |
| W^[1] | (n1, n0) | n1是第一层神经单元数量,nx是输入特征数量 | (4,3) |
| b^[1] | (n1, 1) | n1是第一层神经单元数量 | (4,1) |
| Z^[1] | (n1, m) | n1是第一层神经单元数量,m是样本数量 | (4,m) |
| A^[1] | (n1, m) | n1是第一层神经单元数量,m是样本数量 | (4,m) |
| W^[2] | (n2, n1) | n2是第二层神经单元数量,n1是第一层神经单元数量 | (1,4) |
| b^[2] | (n2, 1) | n2是第二层神经单元数量 | (1,1),即一个实数 |
| Z^[2] | (n2, m) | n2是第二层神经单元数量,m是样本数量 | (1,m) |
| A^[2] | (n2, m) | n2是第二层神经单元数量,m是样本数量 | (1,m) |
5、反向传播:用梯度下降法处理单隐层神经网络
只给结果,推导过程在吴恩达深度学习视频3.10.
下图左边是单个样本的梯度下降,右边是向量化之后的一组样本的梯度下降法。
反复运用以下规则更新W^[1], b^[1], W^[2], b^[2],作业里迭代了10000次,learning_rate =1.2.
W1 -= learning_rate * dW1
b1 -= learning_rate * db1
W2 -= learning_rate * dW2
b2 -= learning_rate * db26、关于参数W和b的随机初始化
只给结论:不能把W^[1]和W^[2]初始化为全0,不然所有神经单元实质上都在做完全相同的的计算,对输出单元的影响也一样大,因此无论迭代多少次,增加多少神经单元,这些神经单元都是对称的,因为它们始终都在计算同样的函数。
b^[1]和b^[2]可以设为0.
解决方法是:随机初始化所有参数,例如用以下代码生成2*2的随机高斯分布,并将矩阵元素的值乘以0.01,确保初始化的W^[1]的元素值很小。
np.random.randn(2,2) * 0.01确保初始化的W^[1]的元素值不能很大,其原因是:
如果W^[1]很大,通过z^[1]=W^[1]X+b^[1]计算得到 的z就会很大或很小,通过a^[1]=g^[1](z^[1])得到的激活值都落入了梯度几乎为0的区间(如下图),此时sigmoid或者tanh激活函数接近饱和,减慢学习速度。
如果不用sigmoid或者tanh激活函数则另当别论,但做二元分类时需要用sigmoid函数做输出层,因此就不应该把W设太大,在单隐层神经网络中,一般用0.01,更多层时需要做其他选择。