人工智能-聚类算法、误差评估、算法优化、特征降维
1、聚类算法简介
典型的无监督算法，主要用于将相似的样本自动归到一个类别中。
根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果。常用的相似度计算方法是欧式距离法
聚类算法与分类算法的区别：
聚类算法是无监督的学习算法，而分类算法属于监督学习。
2、聚类算法API
API：sklearn.cluster.KMeans(n_clusters=8)
参数：n_clusters要聚类的中心数，默认值8
调用方法：estimator.fit(x)、estimator.predict(x)、estimator.fit_predect(x)-指先fit再预测
2.1案例
import matplotlib.pyplot as plt
#from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
#from sklearn.metrics import calinski_harabaz_score
#创建数据
x,y = make_bloks(n_samples=1000,n_features=2,centers=[[-1,-1],,[0,0],[1,1],[2,2]],cluster_std=[0.4,0.2,0.2,0.2],random_state=9)
#生成1000个数，两个特征值，4个中心点，标准差越大越离散，
plt.scatter(x[:,0],x[:,1],marker="o")
plt.show()
#kmeans训练且可视化
y_pre = KMeans(n_clusters=2,random_stats=9).fit_predict(x)
#可视化展示
plt.scatter(x[:,0],x[:,1],c=y_pre)
plt.show()
#用cn_sccie查看最后效果
print(calinski_harabaz_score[x,y_pre]) #评估函数越大越好，输出：3116
3、聚类算法实现流程
3.1思路
K-初始中心点个数
means - 中心点到其他数据点距离的平均值
流程：
- 随机设置k个特征空间内的点作为初始的聚类中心
- 对于其他每个点，计算到这k个中心的距离，最近的中心作为标记类别
- 对已经标记好类别后，重新计算出每个聚类的心中心点（平均值）
- 如果计算得到的新中心点与原中心点一样则结束，否则重新回到第二步
在大规模数据集上，K-Means的收敛速度比较慢
K-Means一点会停止迭代的
4、误差评估
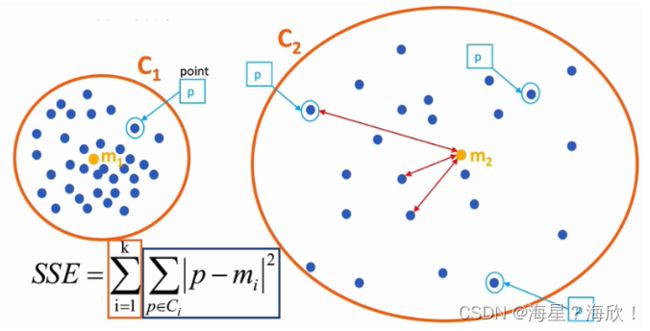
4.1误差平方和
K-Means中的SSE：
SSE越小越好
缺点：
4.2 肘方法–确定K值
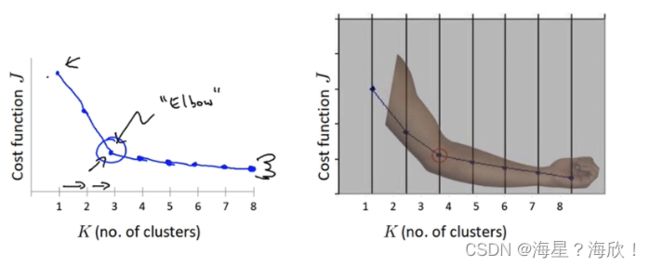
横轴：k值，纵轴：方差
取拐点的k值
4.3 轮廓系数法
S越接近1，效果越好。越接近-1，效果越不好
使得内部距离最小化，外部距离最大化
4.4 CH系数
迹，对角线元素之和=秩的和
S(K)越大聚类越好
要达到的目的：用尽量少的类别聚类尽量多的样本，同时获得好的聚类效果
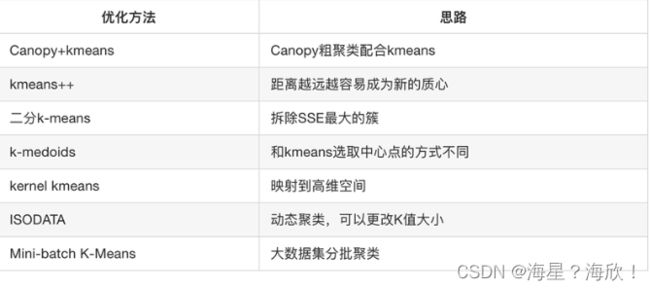
5、算法优化
5.1KMeans算法小结
优点：
- 原理简单，实现容易
- 聚类效果中上（依赖K的选择）
- 空间复杂度o(N),时间复杂度o(lkN)（N为样本点个数，K中心点个数，I迭代次数）
缺点： - 对离群点，噪声敏感
- 结果不一定全局最优，只能保证局部最优（与K值和初始点的选择有关）
- 很难发现大小差别很大的簇及进行增量计算
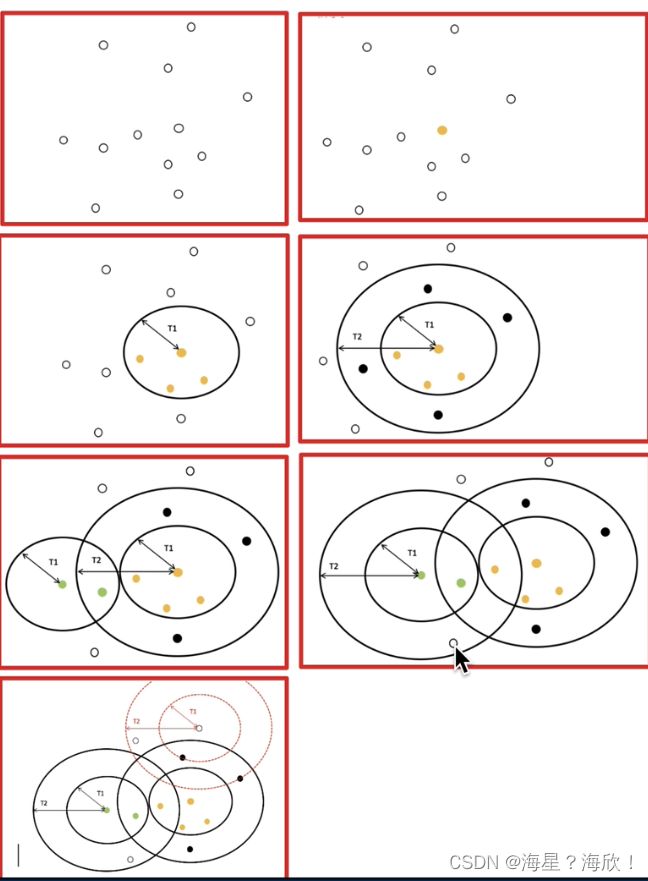
5.2 改进1-Canopy算法
初始中心点的选择：避免离的太近
确定初始点的选择步骤：
先随机一个，然后在外围再选一个
5.3 改进2-K-means++
目的也是让初始中心点尽可能远
5.4 改进3- 二分k-means
步骤：
1，将所有点作为一个簇
2，将该簇一分为二
3，选择能最大限度降低聚类代价函数（即误差平方和）的簇划分为两个簇
4，依次进行下去，直到簇的数目等于用户给定的数目K为止
5.5 改进4-K-medoids
与k-means的区别在于：确定新点时，不是取的平均值，而是取的到其他点的距离之和最小的点
因此，计算量剧增
6、特征降维
6.1 降维定义
降维：在某些特定限定条件下，降低随机变量个数，得到一组"不相关"的主变量的过程
降维的两种方式：特征选择、主成分分析
6.2 特征选择
数据中包含冗余或无关变量（或称特征、属性、指标等），从原特征中找出主要特征
方法：
- Filter过滤式：主要探究特征本身特点、特征与特征和目标值之间关联（方差选择）
- Embedded(嵌入式)：算法自动选择特征
API :
sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
删除所有低方差特征
#删除方差小的列
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
def var_thr():
data = pd.read_csv("./data/factor_returns.csv")
print(data.shape)
transfer = VarianceThreshold(threshold=1)
transfer_data = transfer.fit_transform(data.iloc[:,1:10])
print(transfer_data)
print(data.iloc[:,1:10].shape)
print(transfer_data.shape)
if __name__ == '__main__':
var_thr()
相关系数
皮尔逊相关系数
from scipy.stats import pearsonr
def pea_demo():
x1 = [12.5,13,11.5,11.9,33.5]
x2 = [12,13,11,11,32]
ret = pearsonr(x1,x2)
print("皮尔逊相关系数结果是：\n",ret)
if __name__ == '__main__':
pea_demo()
斯皮尔曼相关系数
from scipy.stats import pearsonr
def spea_demo():
x1 = [12.5,13,11.5,11.9,33.5]
x2 = [12,13,11,11,32]
ret = spearmanr(x1,x2)
print("斯皮尔曼相关系数结果是：\n",ret)
if __name__ == '__main__':
pea_demo()
6.3 主成分分析
高维数据转化为低维数据
def pca_demo():
data = [[2,8,4,5],[6,3,0,8],[5,4,9,1]]
transfer = PCA(n_components=0.9)
trans_data = transfer.fit_transform(data)
print('保留0.9的数据最后维度为：\n',trans_data)
transfer2 = PCA(n_components=3)
trans_data = transfer2.fit_transform(data)
print('降到3维度的结果为：\n',trans_data)
if __name__ == '__main__':
pca_demo()
7、探究用户对物品类别的喜好
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
#获取数据
order_product = pd.read_csv('./order_products_prior.csv')
products = pd.read_csv('./products.csv')
orders = pd.read_csv('./order_products_prior.csv')
aisles = pd.read_csv('./aisles.csv')
order_product.head()
# 合并表格
table1 = pd.merge(order_product,products,on=['product_id','product_id'])
table2 = pd.merge(table1,orders,on=['order_id','order_id'])
table = pd.merge(table2,aisles,on=['aisles_id','aisles_id'])
table.shape
#交叉表合并
pd.crosstab(table['user_id'],table['aisle'])
data.shape
#数据截取
new_data= data[:1000]
#特征工程-pca
transfer = PCA(n_components=0.9)
trans_data = transfer.fit_transform(new_data)
trans_data.shape
#k-means
estimator = KMeans(n_clusters=5)
y_pre = estimator.fit_predict(trans_data)
#模型评估
silhouette_score(trans_data,y_pre)