【建议收藏】机器学习数据预处理（五）——特征选择（内附代码）

引言

之前我们介绍了数据预处理的多个前置步骤，包括缺失值处理，异常值处理，特征构造等，感兴趣可以点击下方链接支持一下：

• 【建议收藏】机器学习数据预处理（一）——缺失值处理方法（内附代码）
• 【建议收藏】机器学习数据预处理（二）——异常值处理方法（内附代码）
• 【建议收藏】机器学习数据预处理（三）——数据分桶及数据标准化（内附代码）
• 【建议收藏】机器学习数据预处理（四）——特征构造（内附代码）

特征选择

在进行了数据预处理以及特征构造后，我们需要对所有特征做一个选择，选择其中对模型更重要的特征。

特征选择的方法主要分为三大类的方法，分别是过滤法，包裹法，嵌入法。

接下来我将使用天池学习赛中二手车数据集做示例数据，编写代码，若需要该数据集可以点击主页查看我的其它文章，也可以私信我。

过滤法

该类方法主要是根据不同的特征的不同表现，不讨论其对模型的影响，主要从其与目标的相关性或自相关性等属性来观察其是否是有用的特征。

• 优点：计算较为简单。
• 缺点：没有对后续不同的学习模型进行选择，可能导致其错过更有效地特征。

当使用过滤法进行特征选择的时候，我们可以从其自身角度或者其与其他特征相关性的角度分别来看。

单变量自身情况

这部分主要是从变量本身的出现频次，及其自身能够反映变化的量来决定观察其是否能够作为有效的特征。

• 缺失百分比

若某一特征存在过多缺失值，则可以考虑直接将该特征删除。
读取数据后直接调用isnull().sum()两个方法既可以观察到所有特征的缺失数目，若缺失的比例过大既可以考虑删除。

train_data.isnull().sum()

结果如下：

• 方差

若某连续变量的方差过小，说明该特征值趋向于单一的状态，变化幅度不大，所以可以考虑删除。
在使用pandas读取数据后，直接调用函数就能查看所有列的方差，代码如下。

train_data.std()

结果如下：

上述结果中，方差较小的特征已经被红圈标出，此时就可以把方差为0的特征直接删除，因为他没有变化对我们没有意义，其他的可以酌情删除。

• 频数

若某特征的样本分布更多的偏向于某一值，则可以考虑删除。
在下面的代码示例中，我随机选择了两个特征作为图的数据：

for col in ['seller', 'fuelType']:
    plt.figure()
    plt.title(col)
    train_data[col].value_counts().plot.bar()

结果如下：


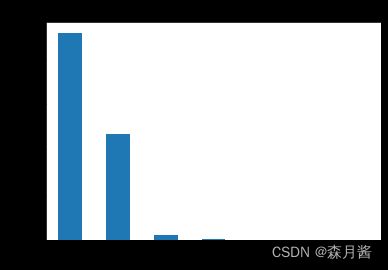
我们可以看到，seller特征的频数上来看，为1的条目相对于为0的少很多，所以可以考虑删除此列。

多变量

多变量之间的关系，主要存在两种：

• 自变量与自变量：若两自变量相关性过高，则会引发多重共线问题，导致模型的拟合效果不好，所以可以在两个自变量相关性较高时选择其中一个自变量。
• 自变量与因变量：相关性越高说明其更能够对于目标来说更重要，更能反应变量的变化原因，建议保留该种变量，反之则建议删除。

于此同时，由于变量又有连续性和类别型两种类型，所以根据不同种类型的变量我们要使用不同的方法：

• 连续型变量间的相关性
  • 皮尔逊相关系数
    该相关系数假设两变量都服从正态分布，其计算方法为两个变量的协方差除以两变量的标准差乘积，能够反映两变量的相关程度。取值范围为[-1,1],绝对值越大说明相关性越大，正负号表示正相关或负相关。

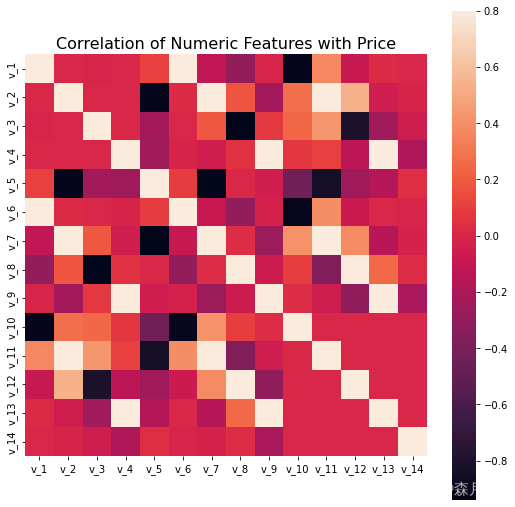
使用pandas中的函数即可满足我们此需求，代码如下所示：

train_data.loc[:,'v_1':].corr('pearson')

结果如下:

也可以将此处的结果可视化出来：

correlation = train_data.loc[:,'v_1':].corr('pearson')

f , ax = plt.subplots(figsize = (9, 9))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square = True,  vmax=0.8)

结果如下：

- 斯皮尔曼相关系数
该相关系数不假设变量服从何种分布，其基于等级的概念计算变量的相关性，更适合顺序变量。
代码如下所示：

correlation = train_data.loc[:,'v_1':].corr('spearman')

结果如下:

可视化结果如下所示，其中代码和上述皮尔逊相关系数类似：

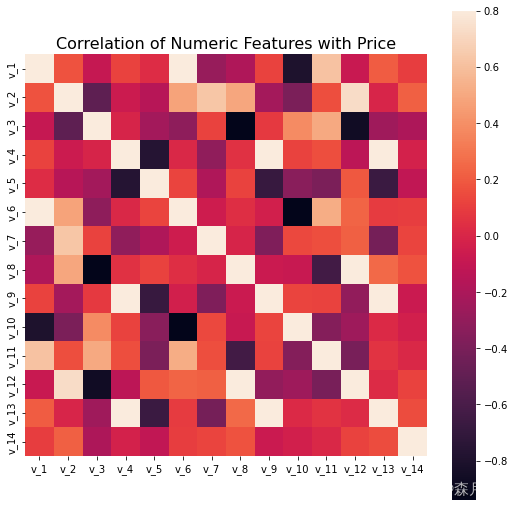
• 连续变量与类别变量间的相关性
  • 肯德尔等级相关系数
    Kendall系数会对按类别变量对样本排序，若排序后，类别特征和连续变量相同，则Kendall系数为1，两变量正相关。若类别特征和连续变量完全相反，则系数为-1，完全负相关。

pandas里也提供了相关方法：

print(train_data['price'].corr(train_data['gearbox'], method='kendall'))
print(train_data['fuelType'].corr(train_data['price'], method='kendall'))
print(train_data['bodyType'].corr(train_data['price'], method='kendall'))

结果如下：

• 类别变量与类别变量间的相关性
  • 卡方验证
    卡方验证能够检验两个类别变量之间的关系，代码如下:

stats.chisquare(train_data['fuelType'],train_data['gearbox'],)

我在执行这部分代码的时候遇到了以下错误： For each axis slice, the sum of the observed
frequencies must agree with the sum of the expected frequencies to a
relative tolerance of 1e-08, but the percent differences are:
0.6395233979503643

• 互信息
  互信息能够衡量两个向量之间的依赖程度，代码如下：

mutual_info_score(train_data['gearbox'], train_data['fuelType'])

包裹法

包裹法利用学习器的性能当作特征的评价标准，根据学习器的学习结果作为特征的选择标准。

完全搜索

便利所有特征子集的组合情况，然后让模型学习。这种方法开销较大，会花费非常长的时间。

启发式搜索

不断改变搜索的空间，根据模型的最终得分作为评分权重。

• 向前/向后搜索

向前搜索和向后搜索是两个完全相反的方向，向前搜索将从空集开始不断地加入新的特征，若评分提高则保留，否则删去。向后搜索从所有特征开始，不断地删除特征迭代。

• 递归特征消除
  递归特征消除简称RFE(Recursive Feature Elimination)，RFE是使用一个基模型进行多轮训练，每轮训练后，消除若干低权值(例特征权重系数或者特征重要性)的特征，再基于新的特征集进行下一轮训练。
  代码实现如下所示：

from sklearn.linear_model import LinearRegression
lr = LinearRegression()


from sklearn.feature_selection import RFE
rfe = RFE(estimator = lr,           # 基分类器
          n_features_to_select = 5,  # 选择特征个数
          step = 1,                  # 每次迭代移除的特征个数 
          verbose = 1                # 显示中间过程
          ).fit(train_data.loc[:1000,'v_0':],train_data.loc[:1000,'price'])
X_RFE = rfe.transform(train_data.loc[:1000,'v_0':])
print("-----RFE特征选择结果-----")
print("有效特征个数 : %d" % rfe.n_features_)
print("全部特征等级 : %s" % list(rfe.ranking_))

结果如下：

PRECV在PRE的基础上加入了模型表现得考虑，使得选择的模型更具有说服力。
代码实现如下所示：

from sklearn.model_selection import StratifiedKFold
from sklearn.feature_selection import RFECV
rfecv = RFECV(estimator=lr,          # 学习器
              min_features_to_select=5, # 最小选择的特征数量
              step=1,                 # 移除特征个数
              cv=StratifiedKFold(3),  # 交叉验证次数
              scoring='r2',     # 学习器的评价标准
              verbose = 1,
              n_jobs = 1
              ).fit(train_data.loc[:100000,'v_0':],train_data.loc[:100000,'price'])
X_RFECV = rfecv.transform(train_data.loc[:100000,'v_0':])
print("RFECV特征选择结果——————————————————————————————————————————————————")
print("有效特征个数 : %d" % rfecv.n_features_)
print("全部特征等级 : %s" % list(rfecv.ranking_))

结果如下：

随机搜索

• 随机特征子集
  随机选择多个特征子集，然后对其表现进行评估，选择评分高的特征子集。
• Null Importance
  Kaggle GM Olivier提出Null Importance特征挑选法能够从一定角度上筛选出真正强壮的特征。

嵌入法

特征选择的过程直接在学习器中完成，把特征选择作为学习器的一部分。
代码如下：

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import GradientBoostingClassifier
 
 
iris = load_iris()
 
 
# 将待L1惩罚项的逻辑回归作为基模型的特征选择
selected_data_lr = SelectFromModel(LogisticRegression(penalty='l1', C = 0.1, solver = 'liblinear'), max_features = 3).fit_transform(iris.data, iris.target)
 
 
# 将GBDT作为基模型的特征选择
selected_data_gbdt = SelectFromModel(GradientBoostingClassifier(), max_features = 3).fit_transform(iris.data, iris.target)
 
 
print(iris.data.shape)
print(selected_data_lr.shape)
print(selected_data_gbdt.shape)

总结

本篇文章列举了常见的特征选择方式和方法，还有一部分代码在更新中。本文部分内容来源于Datawhale中，我再也持续的学习其内容并进行一定的总结，如若侵权请联系删除。