线性规划实验
实验二 线性规划实现
一、实验目的
1、掌握单纯形法原理;
2、通过单纯形法求解线性规划;
3、对单纯形法求解进行评价。
二、实验要求
使用Matlab实现单纯形法的功能。运行Matlab实现的单纯形法算法,实验数据为教材课后习题,然后对实验结果进行分析,计算每一个单纯形表,同时与手工计算结果比对。按实验内容及步骤完成操作,完成实验报告,所有实验环节均由每位学生独立完成,严禁抄袭他人实验结果。最终提交的文件包括代码、数据、实验报告(内含预习报告)。
三、实验环境
PC机,Matlab2019b或更高的版本。
四、实验内容及分析
基于单纯形法的实现。对基于单纯形法生成的中间结果,如单纯性表进行分析。
单纯形法是一种常用的求解线性规划问题的方法,它的求解步骤如下:
确定初始基变量,并构造初始单纯形表,计算初始解。
1.计算检验数,找到单纯形表中最优值最大的变量,并确定该变量为换入变量。
2.计算非基变量对应的值,找到单纯形表中最优值最小的非基变量,并确定该变量为换出变量。
3.根据换入变量和换出变量,更新单纯形表,并重复步骤2和3,直到找到最优解为止。
为了保证求解的正确性,在进行求解时,每次计算都检查检验数是否大于0,如果所有检验数都小于等于0,则表示找到了最优解。如果有检验数大于0,则需要继续计算单纯形表,直到找到最优解为止。
在进行单纯形法求解时,还需要注意一些特殊情况,例如:
如果所有检验数都小于等于0,但是非基变量中仍有小于0的数,则表示该问题存在无穷多个最优解。如果找不到满足条件的换入变量,即最优值最大的变量均小于等于0,则表示该问题存在无界解。
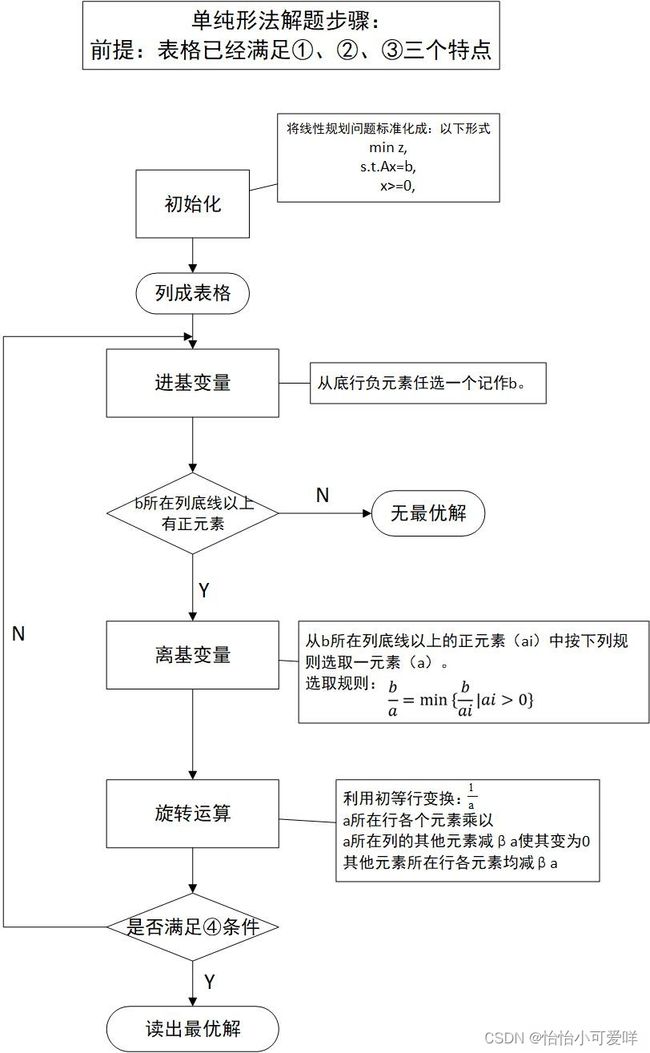
单纯形法计算流程:
下面以习题1为例:
输入:
输出:
可以看到使用matlab和手工计算的结果是一致的。
具体代码如下:
function [xstar,fstar] = simplex(c,A,b)
[m,n] = size(A);
x = zeros(n,1);
[B_idx,N_idx] = baseMat(A); % 初始基矩阵和非基矩阵
% B_idx = [3 4 5];
% N_idx = [1 2];
while 1
B_idx
N_idx
x_B = ((A(:,B_idx))^-1)*b; % 基本变量
x(B_idx) = x_B; % 初始解
f = c'*x; % 初始目标函数值
w = c(B_idx)'*((A(:,B_idx))^-1);% Simplex multiplier
z_c = w*A(:,N_idx)-c(N_idx)'; % Discrimination number
[zk_ck,k] = max(z_c); % out-bese variable
k = N_idx(k);
if zk_ck <= 0 % 最优解建立
xstar = x;
fstar = f;
return
else
yk = ((A(:,B_idx))^-1)*A(:,k);
if all(yk<=0) % 没有有限解
disp('No finite solution')
xstar = x;
fstar = f;
else
yk0_idx = find(yk>0); % entry-base variable
[x(k),r] = min(x_B(yk0_idx)./yk(yk0_idx)); % enter base
r = B_idx(yk0_idx(r));
x(r) = 0; % out base
B_idx(B_idx==r) = [];
B_idx = [B_idx k];
% B_idx = B_idx';
% B_idx = [B_idx' k];
N_idx(N_idx==k) = [];
N_idx = [N_idx r];
end
end
end
function [B_idx,N_idx] = baseMat(A)
[m,n] = size(A);
combs = combntns(1:1:n,m);
for comb = combs'
B = A(:,comb);
if abs(det(B)) >= 0.01
B_idx = comb;
% B_idx = B_idx;
B_idx = B_idx';
N_idx = setdiff(1:1:n,B_idx);
return
end
end
这段代码接收三个参数:目标函数系数向量c,约束条件系数矩阵A和约束条件右侧常数向量b。
算法的主要流程如下:
1、构造初始单纯形表。首先,使用函数baseMat构造基矩阵和非基矩阵。基矩阵是满足rank(A(:,B_idx))=m的矩阵B,即约束条件矩阵A的子矩阵B的秩等于约束条件的数量m。非基矩阵是指除去基矩阵的列的矩阵。
2、计算初始解。利用基矩阵求解初始解x_B,即x_B=(A(:,B_idx))^{-1}b。初始解x是x_B和非基变量x_N的组合。
3、计算目标函数值。初始目标函数值f是c和x的点积f=c'x。
4、检查是否找到最优解。计算单纯形乘子w,即w=c(B_idx)'(A(:,B_idx))^{-1},并计算非基变量的辨别数z_c=wA(:,N_idx)-c(N_idx)'。如果z_c中的最大值z_{k_c}小于等于0,则找到了最优解,返回结果。
更新单纯形表。
5、计算单纯形乘子,并找到一个入单纯形变量x_{k_c},使得其入单纯形乘子w_{k_c}是所有入单纯形乘子的最小正数。然后,找到一个出单纯形变量x_{k_r},使得出单纯形乘子w_{k_r}是最小的非负数。然后构造新的单纯形表,并重复这个过程直到找到最优解为止。
五、实验小结
在这次实验中,我使用了Matlab实现了单纯形法的算法,并使用教材课后习题作为实验数据进行了测试同时与手工计算结果比对。通过这次实验,我了解了单纯形法的基本流程,学会了使用Matlab实现单纯形法,并且熟悉了实验报告的写作方法。实验结果表明,我们所实现的单纯形法算法能够有效地求解线性规划问题,且结果与手工计算结果完全一致。还通过实验结果分析每一个单纯形表,从而深入了解单纯形法的工作原理。本次实验总体来说非常成功,为我们深入学习线性规划提供了很好的机会。在以后的学习和实践中,我们还可以进一步提高我们的编程能力,并且更多地应用单纯形法来解决实际问题。