【论文笔记】Towards Certifying l-infinity robustness using neural networks with l-infinity-dist neurons

引流　https://www.cnblogs.com/setdong/p/16456887.html

原文地址

slides

GitHub 代码

本文发表于 2021 ICML，提出了一个新颖的神经网络计算方式：对于网络中的每个神经元，不采用传统的线性转换+非线性激活函数的方式，而是计算输入与参数之间的 ${\ell }_{\infty }$-distance，作者将其称为 ${\ell }_{\infty }$-dist net，网络中的神经元称为 ${\ell }_{\infty }$-dist neuron。作者理论证明了 ${\ell }_{\infty }$-dist net 具有很好地表达能力（expressivity）和泛化能力（generalization ability），还给出了 ${\ell }_{\infty }$-dist net 在训练中的优化策略。${\ell }_{\infty }$-dist net 还可以作为特征提取器与其他模型结构（如卷积网络）结合使用，实验发现这样的设计在很多数据集上都能获得很好的 certified robustness。

1. ${\ell }_{\infty }$-dist net

1.1) Preliminaries

问题描述 考虑一个标准的分类任务：

• 样本 $x\in \mathcal{X}$ 和相应标签 $y\in \mathcal{Y}=\{1,...,M\}$ 的数据分布为 $\mathcal{D}$，$\mathcal{D}$ 通常是已知的。
• 训练集为 $\tau =\{(x_1,y_1),...,(x_n,y_n)\}$，其中 $(x_i,y_i)$ i.i.d. 取自分布 $\mathcal{D}$。
• $f:x\in \mathcal{X}\to \mathcal{Y}$ 是分类器。
• $x^{\prime }=x+\delta$ 是对抗样本。
• 扰动约束：$ϵ$-bounded ${\ell }_{\infty }$-norm constraint（或称为 ${\ell }_{\infty }$ 扰动），即 $||\delta |{|}_{\infty }\le ϵ$。

任务目标： 使用训练集 $\tau$ 学习一个模型，该模型可以抵抗带有任意${\ell }_{\infty }$ 扰动的样本 $(x,y)$，其中$(x,y)\sim \mathcal{D}$。

这需要计算以 $x$ 为中心的、不会改变 $f$ 对它预测的 ${\ell }_{\infty }$-ball 的最大半径（称为 robust radius）：
$$R(f;x,y)=\{\begin{array}{cc}{\inf }_{f(x^{\prime })\ne f(x)}||x^{\prime }-x|{|}_{\infty }& ,f(x)=y\\ 0& ,f(x)\ne y\end{array}\text{\hspace{1em}(1)}$$
但对于标准的 DNNs，robust radius 很难计算，所以转为计算 $R(f;x,y)$ 的下限 $CR(f;x,y)$，称为 certified radius。对于任意的 $f,x,y$ 有 $CR(f;x,y)\le R(f;x,y)$。

1.2) ${\ell }_{\infty }$-dist neurons

图1的左图是传统的卷积神经元计算方式（线性变换+非线性激活函数），右图是 ${\ell }_{\infty }$-dist neuron 的计算方式：
$$u(x,\theta )=||x-w|{|}_{\infty }+b\text{\hspace{1em}(2)}$$
其中 $\theta =\{w,b\}$ 是参数集合。公式（2）本身就是非线性的，所以不需要像传统网络那样添加一个激活函数 $\sigma$。传统神经元使用点积计算来度量 $x$ 与 $w$ 之间的相似度（similarity），同样地，${\ell }_{\infty }$-dist neuron 使用距离公式作为度量，且距离是非负数，值越小表示相似度越强。

1.3) MLP networks using ${\ell }_{\infty }$-dist neurons

考虑将 ${\ell }_{\infty }$-dist neurons 应用于最简单的模型结构 MLP：

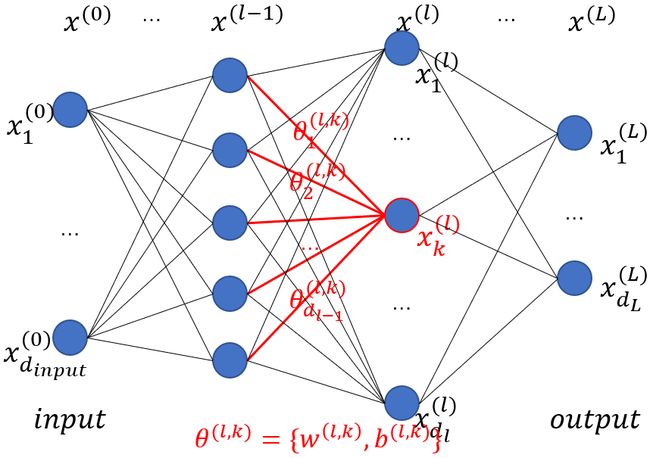
定义一个 $L$ 层的 ${\ell }_{\infty }$-dist net：假设第 $l$ 个隐藏层有 $d_l$ 个隐藏单元，网络的输入为 $x^{(0)}\triangleq x\in {\mathbb{R}}^{d_{input}}$，第 $l$ 个隐藏层中的第 $k$ 个神经元的输出为：
$$x_k^{(l)}=u(x^{(l-1)},{\theta }^{(l,k)})=||x^{(l-1)}-w^{(l,k)}|{|}_{\infty }+b^{(l,k)}\text{\hspace{1em}(3)}$$
其中 $x^{(l)}=(x_1^{(l)},x_2^{(l)},...,x_{d_l}^{(l)})$ 为第 $l$ 层的输出，$1\le l\le L$，$1\le k\le d_l$。

对于 1.1 节描述的分类任务，输出维度 $d_L$ 等于类别 $M$。取网络最后一层的输出的负数用于预测，即 $g(x)=(-x_1^{(L)},-x_2^{(L)},...,-x_M^{(L)})$，预测输出为 $f(x)=\arg {\max }_{i\in [M]}{g}_i(x)$。与标准网络一样，可以对${\ell }_{\infty }$-dist net 使用任何标准的损失函数，比如交叉熵或 hinge loss。

1.4) 1-Lipschitz w.r.t. ${\ell }_{\infty }$-norm

这节首先证明 ${\ell }_{\infty }$-dist net 就是 1-Lipschitz w.r.t. ${\ell }_{\infty }$-norm；然后根据这一性质推导出模型的 certified robustness。

定义： 如果函数 $g(z):{\mathbb{R}}^m\to {\mathbb{R}}^n$ 对任意 $z_1,z_2$ 都满足下式，则 $g(z)$ 被称为 $\lambda$-Lipschitz w.r.t. ${\ell }_p$-norm ($||\cdot |{|}_p$)：
$$||g(z_1)-g(z_2)|{|}_p\le \lambda ||z_1-z_2|{|}_p$$

Fact 1： ${\ell }_{\infty }$-dist net $g(\cdot )$ 是 1-Lipschitz w.r.t. ${\ell }_{\infty }$-norm，即对任意 $x_1,x_2\in {\mathbb{R}}^{d_{input}}$ 都有 $||g(x_1)-g(x_2)|{|}_{\infty }\le ||x_1-x_2|{|}_{\infty }$.
Proof 1： 网络中每个神经元的计算(即公式3)是 1-Lipschitz → 从 $x^{(l)}$ 到 $x^{(l+1)}$ (层到层)的映射是 1-Lipschitz → 整个网络是 1-Lipschitz。

因此，当扰动很小时，输出的变化是有界的，直接约束了 certified radius。

Fact 2： 设 $\mathrm{margin}(x;g)$ 是输出向量 $g(x)$ 中最大元素和第二大元素之间的差，那么对于任意 $x^{\prime }$ 满足 $||x-x^{\prime }|{|}_{\infty }<\mathrm{margin}(x;g)/2$，有 $f(x)=f(x^{\prime })$。即：
$$CR(f,x,y)\ge \mathrm{margin}(x;g)/2\text{\hspace{1em}(4)}$$
Proof 2： $g(x)$ 是 1-Lipschitz，因此当将输入从 $x$ 变为 $x^{\prime }$时，模型输出 $g(x)$ 中的每个元素移动不超过 $\mathrm{margin}(x;g)/2$，那么最大的元素（即预测的类）是不变的。

使用 Fact 2 中的 bound，仅需一次正向传播就能够计算 ${\ell }_{\infty }$-dist net 的 certified robustness，计算成本小。

2. ${\ell }_{\infty }$-dist net 的训练

经验发现传统网络训练方法并不适用于 ${\ell }_{\infty }$-dist net，对此作者提出了一系列相应的优化策略。

2.1) Normalization

问题： 传统网络的线性层的输出是无偏的 unbiased(期望均值为0)，而 ${\ell }_{\infty }$-dist neuron 的输出是有偏的 biased(假设没有bias项 $b$，总是非负的)。这会导致每层的输出会随层数增加而线性增长。

解决方法：
考虑 Batch Normalization (BN)，BN 使用 shift 和 scale 两个操作，但若直接在 ${\ell }_{\infty }$-dist net 中使用 BN 会导致 Lipschitz 常数发生变化(由于 scale 操作)，从而无法保证模型的鲁棒性。

不过作者发现，只使用 shift 操作有助于优化，因此在所有的中间层计算完距离后添加 shift 操作，并移除了 bias 项 $b$（冗余了），但最后一层不做 normalization。与 BN 类似，在 inference 时使用 running mean。

2.2) Smoothed Approximated Gradients

问题： ${\ell }_{\infty }$-dist 的梯度向量(如 $\triangledown_w ||z-w||_\infty $ 和 ${▽}_z||z-w|{|}_{\infty }$)十分稀疏，通常只包含一个非零元素。通过实验观察到，如果直接使用 SGD/Adam 训练(随机初始化的) ${\ell }_{\infty }$-dist net，那么在每个 epoch 中，只有不到 1% 的参数在更新。

解决方法：
用 ${\ell }_p$-dist neuron 替换整个网络的神经元，取得近似的 & 非稀疏的参数梯度。在训练中，最开始时将 $p$ 设置为一个很小的值，在接下来的每次迭代中不断增加 $p$ 的值，直到逼近无穷。在最后几次 epochs 中，将 $p$ 设置为无穷。

2.3) Parameter Initialization

问题： 深层模型的训练准确率比浅层模型的差

解决方法：
参考 ResNet ，可以在初始化 weights 和 biases 时直接构建恒等映射(identity mapping)。具体来说，对于输入-输出维度相同的 ${\ell }_{\infty }$-dist layer，首先用标准高斯分布随机初始化 weights，然后将对角元素（即公式3中的 $w_j^{(l,j)}$，$l$ 层第 $j$ 个神经元与 $l-1$ 层第 $j$ 个神经元之间的weight）修改为一个很大的负数 $C_0$。在实验中作者设置 $C_0=-10$。当应用了 mean shift normalization 后，不再需要添加偏差 biases，并且 running mean 会自动进行恒等映射。

2.4) Weight Decay

问题： 将 Weight Decay 应用到 ${\ell }_{\infty }$-dist net 会使模型的性能变差，可能是由于 Weight Decay 与 ${\ell }_{\infty }$-norm 不兼容。

解决方法：
传统网络的计算方式是点积，所以权重的 ${\ell }_2$-norm 可以控制输出的大小。而 $||w|{|}_2$ 与 ${\ell }_{\infty }$-dist layer 的输出大小无关。所以对于 Weight Decay Regularizer，可以用 $||w|{|}_{\infty }$ 取代 $||w|{|}_2$。类似于 $⟨x,w⟩\le ||x|{|}_2||w|{|}_2$，我们有 $||x-w|{|}_{\infty }\le ||x|{|}_{\infty }+||w|{|}_{\infty }$。

对于训练中的 ${\ell }_p$-dist neurons，使用 ${\ell }_p$-norm regularization。通过对权重 $w$ 的求导，有关权重的 weight decay 公式为：
$${△}_{w_i}=-\lambda {▽}_{w_i}||w|{|}_p^2=-\lambda {\left(\frac{|w_i|}{||w|{|}_p}\right)}^{p-2}{w}_i\text{\hspace{1em}(5)}$$
其中 $\lambda$ 是 weight decay 的系数，当 $p\to \infty$ 时，weight decay 往往只对绝对值最大的元素 $w_i$ 产生影响。

3. 实验

3.1) 实验设置

四个基准数据集：MNIST, Fashion-MNIST, CIFAR-10, TinyImagenet
> 模型配置：
主要研究两种模型：1) 仅 ${\ell }_{\infty }$-dist net；2) ${\ell }_{\infty }$-dist net + MLP：${\ell }_{\infty }$-dist net 作为特征提取器。

• 对于 MNIST 和 Fashion-MNIST，使用 5 层 ${\ell }_{\infty }$-dist net；对于 CIFAR-10 和TinyImageNet，使用 6 层 ${\ell }_{\infty }$-dist net。
• 每个隐藏层包含 5120 个单元。
• 每个中间层都应用 normalization。
• Top 层包含 10 个单元 (TinyImageNet 为 200 个单元)
• 对于 ${\ell }_{\infty }$-dist net + MLP，移除 top 层，并添加传统的全连接层，隐藏层包含 512 个单元，且添加了 tanh 激活函数。
  

> 训练配置:

• optimizer: 使用 Adam, 其中 ${\beta }_1=0.9,{\beta }_2=0.99,ϵ=10^{-10}$.
• data augmentation: 对于 MNIST 和 Fashion-MNIST, 使用随机剪裁 random crop (padding = 1); 对于 CIFAR-10，使用随机剪裁 (padding = 4) 和 random horizontal flip; 对于 TinyImageNet，使用 random horizontal flip, 训练中将每张图剪裁到 $ 56 \times 56$ 像素，测试中使用中心剪裁 center crop.
• 损失函数: 对于 ${\ell }_{\infty }$-dist net, 使用 hinge loss, threshold 超参数 $t$ 取决于 $ϵ$; 对于 ${\ell }_{\infty }$-dist net + MLP, 使用 IBP loss, 涉及两个超参数 $\kappa ,{ϵ}_{train}$.
• 训练过程: 首先, 用 ${\ell }_p$ 代替 ${\ell }_{\infty }$, 并令 $p=8$，此时训练 $e_1$ 个 epochs; 然后逐渐将 $p$ 从 $8$ exponentially 增大到 $1000$, 此时训练 $e_2$ 个 epochs; 最后将 $p$ 设为无穷, 此时训练 $e_3$ 个 epochs. 其中 $e_1,e_2,e_3$ 是超参数, 不同数据集设置的值不同.
• $e_1$ epochs 中 $lr=0.02$, 在接下来的 $e_2,e_3$ epochs 中使用 cosine annealing 降低学习率.
• weight decay: $\lambda =0.005$. 对于 ${\ell }_{\infty }$-dist nets, 使用 ${\ell }_p$-norm weight decay; 对于 MLP, 使用 ${\ell }_2$-norm weight decay.

> Evaluation:
使用两种指标来评估模型的 robustness: 1) robust test accuracy: 使用 PGD 攻击, 攻击步长设为 $20$; 2) certified radius: 计算每个样本的 CR, 并计算在 CR 内的测试样本的百分比. Note: 第二个指标始终 lower than 第一个指标.

> Baselines:
对比了先进的方法, 包括: 1) relaxation methods: CAP, PVT, DiffAI, IBP, CROWN-IBP, CROWN-IBP with loss function, COLT; 2) Lipschitz networks: GroupSort.

3.2) 实验结果:

“Test” 表示干净样本的测试准确率; “Robust” 表示PGD 样本的测试准确率; “Certified” 表示 certified robust 测试准确率. “FLOPs” 表示前向传播中所需的基本浮点运算的数量 (即传统网络中的点积和加法或 ${\ell }_{\infty }$-dist net 中的减法).

> General profermance of ${\ell }_{\infty }$-dist net
从表 1 中可以看到，单独使用 ${\ell }_{\infty }$-dist net 已经在所有数据集上获得了不错的 certified accuracy. 尤其是, 在 CIFAR10 数据集上达到了最好的 certified accuracy，且获得了比其他方法更高的标准准确率(干净样本).
Note: 只使用标准损失函数来训练 ${\ell }_{\infty }$-dist net, 无需任何对抗训练。

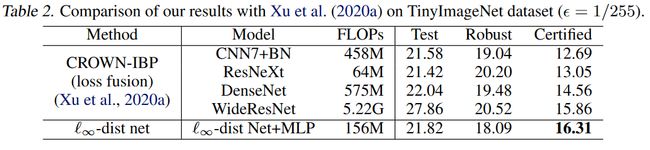
> General profermance of ${\ell }_{\infty }$-dist net + MLP
如表1和表2, 对于所有数据集，${\ell }_{\infty }$-dist net + MLP 比单独的 ${\ell }_{\infty }$-dist net 获得了更好的 certified accuracy.

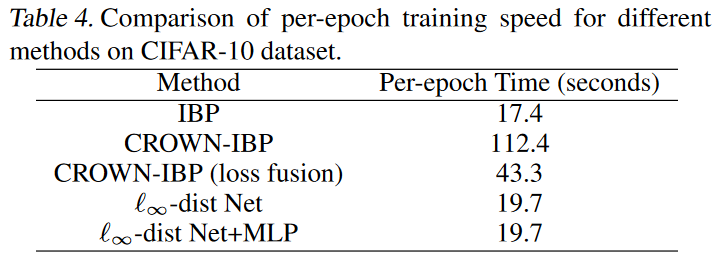
> Efficiency
如表4, 训练和 certification 都很快. 训练 ${\ell }_{\infty }$-dist net 的计算成本与训练相同大小的常规网络大致相同，并且 certification 过程只需要一次向前传播 forward pass.

> 与 GroupSort Network 对比
由于 GroupSort 也使用了1-Lipschitz 且使用标准损失函数训练即可(不需要对抗训练), 作者特别地将这两个模型进行了比较. 在 GroupSort Network 中，所有权重矩阵 $W$ 都被限制为 bounded ${\ell }_{\infty }$-norm，即 $||W|{|}_{\infty }\le 1$，这导致了耗时的 projection 操作, 带来了优化难度，进一步限制了网络结构的可扩展性. 作者将 ${\ell }_{\infty }$-dist net 在 MNIST 数据集上显着优于 GroupSort 的原因也解释为这一点.

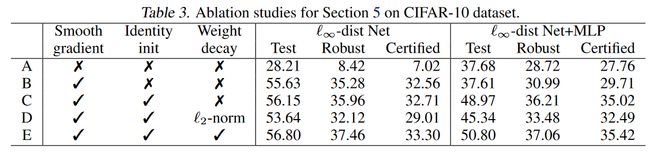
> Ablation Studies
作者还实验观察前述的 smoothed approximated gradients, parameter initialization(使用 identity map 构建) 和 ${\ell }_p$-norm weight decay 的影响, 结果如表 3 所示, 可以看出:

• smoothed approximated gradients 对 ${\ell }_{\infty }$-dist net 的训练十分重要, 添加它后模型的 certified accuracy 可达到 32.56%.
• smoothed approximated gradients 和 parameter initialization 均对 ${\ell }_{\infty }$-dist net+MLP 训练十分重要, 结合它们一同使用后, 模型的 certified accuracy 达到 35.02%.
• ${\ell }_{\infty }$-norm weight decay 可以进一步提升结果，尽管效果可能很小(两个模型的 certified accuracy 分别提高了 0.59% 和 0.4%).
• 传统的 ${\ell }_2$-norm weight decay 会损害 ${\ell }_{\infty }$-dist net 的性能.

总之, 这几个训练策略都对模型的性能有帮助.