机器学习(四)——逻辑回归
机器学习(四)——逻辑回归
文章目录
- 机器学习(四)——逻辑回归
-
- 关于分类问题
- 逻辑回归
-
- 隐含变量模型——probit回归
- 逻辑分布与sigmoid函数
- 逻辑回归
- 多分类问题
-
- one-vs-all
- one-vs-one
- 多元逻辑回归
- 正则化
- 小结
关于分类问题
在前面的博文中,我介绍了线性回归、岭回归、Lasso回归三种回归模型,以及求解机器学习优化问题最重要、应用最广泛的优化算法——梯度下降法。接下来我们把目光投向另一类问题,也是更加广泛的问题——分类问题。
在实际机器学习的应用领域中,我们更多地碰到的是这样的问题,我们通常需要预测的变量并不是连续的,而是离散的,举几个例子:
- 确定一封邮件是否为垃圾邮件;(这一类只有两个可能结果的问题被称为二分类问题)
- 根据医学检测影像判断肿瘤是良性或者恶性;
- 预测一个产品属于优良中差中的哪一等;(这一类有多个可能结果的问题被称作多分类问题)
对于这一类问题,回归模型往往起不到作用,这时我们就需要另一种模型——分类模型。逻辑回归(Logistic Regression)就是一个非常经典的分类模型,
逻辑回归
我们以一个二分类的问题为例,讲解二元逻辑回归的基本原理。假设我们要分析一批学生在概率论与数理统计考试中能否及格。我们目前已经采集到了过去几届的人是否通过的数据,以及他们在大一时的各科成绩。我们希望能通过这些数据建立模型,来预测这一届的学生有哪些可以通过。
隐含变量模型——probit回归
我们已经知道线性回归的方法是不适用的,但我们仍然想要以一种线性的形式来处理这个问题,于是我们考虑将这些数据产生的效应分为两类:
- 一类是正效应,也就是说特征对学生能否通过考试有正面作用,我们记作 y ∗ y^* y∗.
- 另一类是负效应,也就是说特征对学生能否通过考试起负面作用,我们记作 y ∼ y^{\sim} y∼.
为什么这样分类,因为一个特征可能对结果既产生正面效应又产生负面效应。当正面效应大于负面效应时,我们就可以认为他能通过,当负面效应大于正面效应时,我们就认为他不能通过。
设我们有自变量集合 X i ⃗ = ( x i 1 , x i 2 , ⋅ ⋅ ⋅ , x i n ) ( 其 中 i 表 示 数 据 是 第 几 条 ) \vec{X_i}=(x_{i1},x_{i2},···,x_{in})(其中i表示数据是第几条) Xi=(xi1,xi2,⋅⋅⋅,xin)(其中i表示数据是第几条)为了简化,后面分析时,省去下标 i i i。
这时我们进一步假设:正效应和负效应与特征之间成线性关系,再添加上服从正态分布的误差,得到下面的式子: y ∗ = X ⃗ φ ⃗ + θ y^*=\vec{X}\vec{\varphi}+\theta y∗=Xφ+θ y ∼ = X ⃗ ω ⃗ + τ y^{\sim}=\vec{X}\vec{\omega}+\tau y∼=Xω+τ其中 θ \theta θ和 τ \tau τ都是服从正态分布的误差。
在这里引申一下,这里的误差为什么服从正态分布呢?实际上,模型与实际值产生的误差往往是由于我们有很多很多模型未捕捉到的特征造成的,根据中心极限定理,无穷多个随机变量的和的分布服从正态分布,因此我们也可以认为这些误差项近似服从正态分布。
回到原来的推导中来,令 z = y ∗ − y ∼ , γ ⃗ = φ ⃗ − ω ⃗ , ε = θ − τ z=y^*-y^{\sim},\vec{\gamma}=\vec{\varphi}-\vec{\omega},\varepsilon=\theta-\tau z=y∗−y∼,γ=φ−ω,ε=θ−τ,我们可以得到:
z = X ⃗ γ ⃗ + ε z=\vec{X}\vec{\gamma}+\varepsilon z=Xγ+ε y = { 1 , X ⃗ γ ⃗ + ε > 0 0 , e l s e y=\left\{ \begin{aligned} & 1,\vec{X}\vec{\gamma}+\varepsilon>0 \\ & 0,else\\ \end{aligned}\right. y={1,Xγ+ε>00,else再进一步,我们可以得到( y = 1 y=1 y=1)的概率为: P ( y = 1 ) = P ( ε > − X ⃗ γ ⃗ ) = 1 − P ( ε ≤ − X ⃗ γ ⃗ ) = 1 − F ε ( − X ⃗ γ ⃗ ) P(y=1)=P(\varepsilon>-\vec{X}\vec{\gamma})=1-P(\varepsilon\leq-\vec{X}\vec{\gamma})=1-F_\varepsilon(-\vec{X}\vec{\gamma}) P(y=1)=P(ε>−Xγ)=1−P(ε≤−Xγ)=1−Fε(−Xγ)其中, F ε F_\varepsilon Fε为正态随机变量 ε \varepsilon ε的分布函数。这样的数学模型在学术上被称为probit回归。而且我们在研究过程中,假设了两个无法观测的变量 y ∗ , y ∼ y^*,y^\sim y∗,y∼,这种无法观测的变量被称为隐含变量(latent variable),这一类数学模型被称作隐含变量模型(latent variable model)。
probit回归在数学上是比较完美的,但是熟悉正态分布的读者应该知道,这里存在着一个重大的问题:正态分布的分布函数非常复杂,没有解析表达式,因此在工程上难以处理,也很难通过编程去实现,因此我们需要寻求这样一个函数或者一个分布,可以近似地来表示正态分布。后来学术界使用了这样一个分布——逻辑分布。
逻辑分布与sigmoid函数
我们在概率论与数理统计中学到过,正态随机变量在线性变换下保持稳定,因此我们研究正态随机变量时,一般都是把它转化到标准正态分布中研究,接下来我们就来研究如何使用逻辑分布的分布函数去拟合标准正态分布的分布函数。
逻辑分布,又被称为增长分布,标准逻辑分布的分布函数形式是这样的: S ( x ) = 1 1 + e − x S(x)=\frac{1}{1+e^{-x}} S(x)=1+e−x1这个分布函数就是著名的sigmoid函数,这是一个非常重要的函数,在神经网络和深度学习中被广泛使用为激活函数,在这里我们用sigmoid函数去拟合标准正态分布的分布函数,得到结果如下:
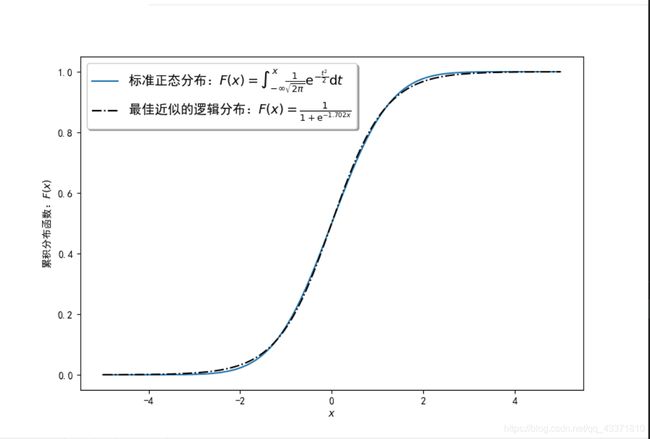
由此我们可以得到: F ε ( σ x + μ ) = ϕ ( x ) = S ( − 1.702 x ) F_\varepsilon(\sigma x+\mu)=\phi(x)=S(-1.702x) Fε(σx+μ)=ϕ(x)=S(−1.702x)
由此,我们可以得到逻辑回归的假设函数: P ( y = 1 ) = 1 1 + e X ⃗ β ⃗ P(y=1)=\frac{1}{1+e^{\vec{X}\vec{\beta}}} P(y=1)=1+eXβ1
其中 β ⃗ = ( β 1 , β 2 , ⋅ ⋅ ⋅ , β n ) \vec{\beta}=(\beta_1,\beta_2,···,\beta_n) β=(β1,β2,⋅⋅⋅,βn),为模型参数。
接下来我们就用机器学习的方法来讨论逻辑回归的问题。
逻辑回归
机器学习有三大要素:假设函数、损失函数和优化算法。在前面我们已经得到了假设函数: H ( X ) = 1 1 + e X ⃗ β ⃗ H(X)=\frac{1}{1+e^{\vec{X}\vec{\beta}}} H(X)=1+eXβ1接下来我们需要考虑使用什么样的损失函数。
对于这样一个二元分类问题,我们希望的是模型预测的结果与真实值越接近越好。用数学的形式来描述:假设模型预测能及格的学生集合为A,实际及格的学生集合为B,我们希望两个集合的交集越大越好。借鉴香农信息论中对于熵的理论,我们采用一种叫做交叉熵(Cross Entropy)的损失函数: L L = − ∑ i { y i l n h ( X i ⃗ ) + ( 1 − y i ) l n [ 1 − h ( X ⃗ ) ] } LL=-\sum_i\{y_ilnh(\vec{X_i})+(1-y_i)ln[1-h(\vec{X})]\} LL=−i∑{yilnh(Xi)+(1−yi)ln[1−h(X)]}交叉熵是一种在分类问题中非常常用的损失函数,它可以近似地被看作两个概率分布之间的距离。
得到了损失函数后,我们就可以使用梯度下降法或者随机梯度下降法对这个问题进行处理,有关梯度下降法和随机梯度下降法的内容,可以参考我前面的博客。机器学习(三)——梯度下降法
多分类问题
刚才我们讨论了二分类问题,而现实中的情况有时并非如此,很多时候我们要分类的类别不止两个,这时我们就需要应用一些方法对多分类问题进行分解,或者将模型推广到多元的形式。这里介绍针对多分类问题的三种解决方案。
one-vs-all
one-vs-all方法,有时也称为one-vs-rest方法,简称OvA或OvR,是最广泛使用的用逻辑回归来解决多元分类问题,它的思想其实很简单:假设目标有 k k k个可能的分类,对于每一个分类,我们都构造一个二分类的逻辑回归模型,判断它是否属于这个类别,那么模型输出的0和1就变成了如下的含义:
对于第 i i i个分类:
- 0:模型认为,这个样本不属于这个类别;
- 1:模型认为,这个样本属于这个类别;
这样,我们只需要使用 ( k − 1 ) (k-1) (k−1)个二元逻辑回归分类器,逐一判断它是否属于某个类别,最终就可以确定它属于何种类别。这种处理方法既简单又实用,于是被广泛应用。
one-vs-one
one-vs-one方法其实与one-vs-all非常类似。它是把 k k k元分类问题中的类别两两组合,根据组合数公式可知,一共可以分解成 k ( k − 1 ) / 2 k(k-1)/2 k(k−1)/2个二元分类问题,最后采用一种类似投票的方式,由这些二元分类器来选出最符合的类别。
这种方法在一定程度上可以减少过拟合,提升模型效果,但是由于需要训练的模型比OvA要多,所以训练速度会相应减慢。
多元逻辑回归
多元逻辑回归的方法就是相当于把模型从二元往多元方向上推广。数学推导的总体思路与二元逻辑回归类似,构造隐含变量然后利用正态分布的知识去近似或者求解概率。由于推导较复杂这里不再赘述,我们只看一下结论: { P ( y = 1 ) = e X ⃗ β 1 ⃗ / ( 1 + ∑ j = 1 k − 1 e X ⃗ β j ⃗ ) P ( y = 2 ) = e X ⃗ β 2 ⃗ / ( 1 + ∑ j = 1 k − 1 e X ⃗ β j ⃗ ) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ P ( y = 0 ) = 1 / ( 1 + ∑ j = 1 k − 1 e X ⃗ β j ⃗ ) \left\{ \begin{aligned} & P(y=1)=e^{\vec{X}\vec{\beta_1}}/(1+\sum_{j=1}^{k-1}e^{\vec{X}\vec{\beta_j}})\\ & P(y=2)=e^{\vec{X}\vec{\beta_2}}/(1+\sum_{j=1}^{k-1}e^{\vec{X}\vec{\beta_j}})\\ & ······\\ & P(y=0)=1/(1+\sum_{j=1}^{k-1}e^{\vec{X}\vec{\beta_j}})\\ \end{aligned}\right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧P(y=1)=eXβ1/(1+j=1∑k−1eXβj)P(y=2)=eXβ2/(1+j=1∑k−1eXβj)⋅⋅⋅⋅⋅⋅P(y=0)=1/(1+j=1∑k−1eXβj)然后我们可以采用参数估计中的最大似然估计法,将所有样本及其对应概率全部乘起来,求导令它为零得到参数的估计值。
正则化
在逻辑回归中,我们也可以通过减去参数和的绝对值或参数的平方和的方法来防范过拟合,也就是通过正则化方法来防止过拟合,这部分与岭回归和Lasso回归完全类似,这里不再过多赘述。参考:机器学习(二)——线性回归的进一步讨论
小结
本文主要介绍了一种经典且常用的分类模型——逻辑回归。有意思的是,由于历史原因,虽然逻辑回归的名字中带有“回归”,但它却不是处理回归问题的模型。在下一篇文章中,我将就分类问题进一步进行讨论,介绍几个常用的分类模型。