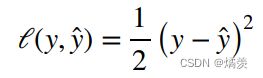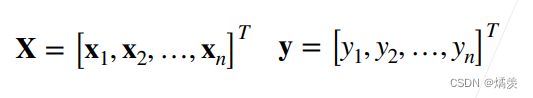深度学习笔记4：线性回归+基础优化方法

线性回归

应用：如何在美国买房（房价预测问题）

房价预测

一个简化模型

• 假设1：影响房价的关键因素是卧室个数、卫生间个数、居住面积，记为x₁，x₂，x₃

• 假设2：成交价是关键因素的加权和（权重和偏差的实际值在后面决定）

  

线性模型

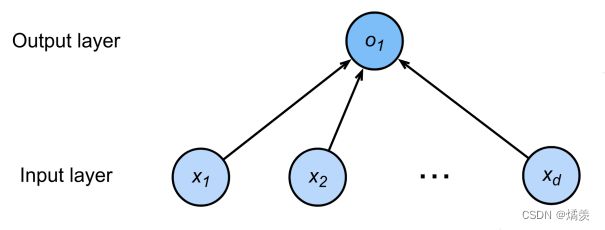
• 给定n维输入x = [x₁ , x₂ , …, x_n ]^T

• 线性模型有一个n维权重和一个标量偏差w = [w₁ ,w₂ , …,w_n ] ^T , b

• 输出是输入的加权和y = w₁x₁ + w₂x₂ + … + w_n x_n + b

  向量版本：y = ⟨w, x⟩ + b

线性模型可以看做是单层神经网络

神经网络源于神经科学

衡量预估质量

• 比较真实值和预估值，例如房屋售价和估价

• 假设y是真实值，ŷ是估计值，我们可以比较

  

  这个叫做平方损失

训练数据

• 收集一些数据点来决定参数值（权重和偏差）例如：过去6个月卖的房子
• 这被称之为训练数据
• 通常越多越好
• 假如我们有n个样本，记[外链图片转存失败,源站可能有防盗链机制,建议将

参数学习

• 训练损失

  

• 最小化损失来学习参数

  

显式解

• 将偏差加入权重

  

• 损失是凸函数，所以最优解满足

  

总结

• 线性回归是对n维输入的加权，外加偏差
• 使用平方损失来衡量预测值和真实值的差异
• 线性回归有显式解
• 线性回归可以看做是单层神经网络

基础优化方法

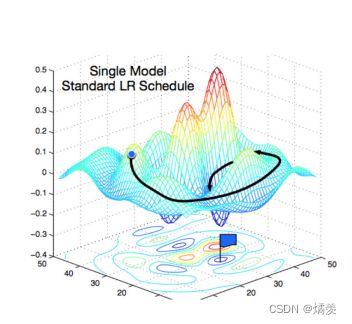
梯度下降

• 挑选一个初始值w₀

  

• 重复迭代参数t=1，2，3

  

  沿梯度方向将增加损失函数值

  学习率：步长的超参数

选择学习率

不能选太小，选小的值，重复步骤太多了；不能选太大，选大的值，可能一直在振荡，并没有下降

小批量随机梯度下降

• 在整个训练集上算梯度太贵：一个深度神经网络模型可能需要数分钟至数小时

• 我们可以随机采样b个样本i₁，i₂， …，i_b来近似损失

  

  b是批量大小，另一个重要的超参数

选择批量大小

• 不能太小：每次计算量太小，不适合并行来最大利用计算资源
• 不能太大：内存消耗增加浪费计算，例如如果所有样本都是相同的

总结

• 梯度下降通过不断沿着反梯度方向更新参数求解
• 小批量随机梯度下降是深度学习默认的求解算法
• 两个重要的超参数是批量大小和学习率

代码实现：

1 线性回归的从零开始实现

我们将从零开始实现整个方法，包括数据流水线、模型、损失函数和小批量随机梯度下降优化器

%matplotlib inline 
#在plot默认嵌入matplotlib里
import random #随机梯度下降 初始化权重
import torch
from d2l import torch as d2l

根据带有噪声的线性模型构造一个人造数据集。 我们使用线性模型参数w=[2,−3.4]^⊤、b=4.2和噪声项ϵ生成数据集及其标签：
$$y=Xw+b+ϵ$$

def synthetic_data(w, b, num_examples):  
    """生成 y = Xw + b + 噪声。"""
    X = torch.normal(0, 1, (num_examples, len(w))) #生成均值为0、方差为1的随机数，大小为样本数，列数是w的长度的X
    y = torch.matmul(X, w) + b #y=y=Xw+b
    y += torch.normal(0, 0.01, y.shape) #加上随机噪音，均值为0、方差为0.01，形状与y相同的ϵ
    return X, y.reshape((-1, 1)) #返回X，列向量的y

true_w = torch.tensor([2, -3.4]) #真实w
true_b = 4.2 #真实b
features, labels = synthetic_data(true_w, true_b, 1000) #生成features特征和labels标注

features 中的每一行都包含一个二维数据样本，labels 中的每一行都包含一维标签值（一个标量）

print('features:', features[0], '\nlabel:', labels[0]) #打印第0个样本和标号

结果：

features: tensor([-0.8274, -0.0053])
label: tensor([2.5762])

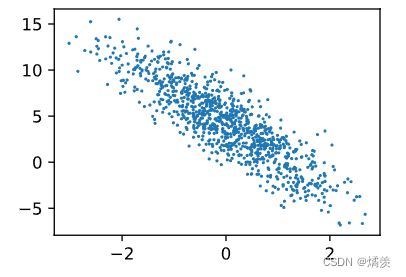
#用图表示
d2l.set_figsize() #设置图表大小
d2l.plt.scatter(features[:, 1].detach().numpy(), 
#特征的第一列 （detach：需要从计算图中detach出来才能转换为numpy）
                labels.detach().numpy(), 1); #标号 

结果：

定义一个data_iter 函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量

def data_iter(batch_size, features, labels): #输入：批量大小 特征 标号
    num_examples = len(features) #样本数
    indices = list(range(num_examples)) #生成对每个样本的indices （range：从0到n-1的样本变成python的list）
    random.shuffle(indices) #打乱下标，就可以随机顺序访问样本
    for i in range(0, num_examples, batch_size):
        
        batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)]) #得到i到i+batch_size随机的批量大小的indices
        #之所以用min是如果样本数不能整除批量大小的时候，应该取到最后一个样本
        yield features[batch_indices], labels[batch_indices] #产生一个随机顺序的特征和对应标号  
        #yield：python的返回函数

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y) #得到X（10 X 2）的一个tensor y(10 X 1)的向量
    break

结果：

tensor([[ 0.4302, -0.7588],
[-0.4263, -0.1673],
[ 0.1022, -0.4205],
[-1.1555, 1.1995],
[-0.4798, 1.7720],
[-0.1007, -0.1337],
[ 1.7665, 0.8338],
[-0.4435, -0.9913],
[ 2.4515, -0.1871],
[-0.9225, -0.2273]])
tensor([[ 7.6388],
[ 3.9031],
[ 5.8427],
[-2.1921],
[-2.7899],
[ 4.4388],
[ 4.9068],
[ 6.6866],
[ 9.7463],
[ 3.1313]])

定义 初始化模型参数

w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True) 

定义模型

def linreg(X, w, b):  
    """线性回归模型。"""
    return torch.matmul(X, w) + b  #y=xw+b

定义损失函数

def squared_loss(y_hat, y):  
    """均方损失。"""
    return (y_hat - y.reshape(y_hat.shape))**2 / 2 #y_hat为预测值，y为真实值；并未求均值

定义优化算法

def sgd(params, lr, batch_size):  #params给定所有参数list包含w b
    """小批量随机梯度下降。"""
    with torch.no_grad(): #不计算梯度
        for param in params:
            param -= lr * param.grad / batch_size #梯度是会存在.grad中；求均值
            param.grad.zero_() #梯度设为0；当下次计算不用和这次相关了

训练过程

lr = 0.03 #学习率
num_epochs = 3 #扫描数据次数
net = linreg #模型
loss = squared_loss #均方损失

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels): #每次用批量大小的X,y
        l = loss(net(X, w, b), y) #X和y的小批量损失
        #l形状是（batch_size,1）,而不是一个标量。所有的元素被加到一起并以此计算关于[w,b]的梯度
        l.sum().backward() #求和之后算梯度
        sgd([w, b], lr, batch_size) #使用参数的梯度优化更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels) 
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

结果：

epoch 1, loss 0.033446
epoch 2, loss 0.000116
epoch 3, loss 0.000050

比较真实参数和通过训练学到的参数来评估训练的成功程度

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

结果：

w的估计误差: tensor([-9.3460e-05, -4.0102e-04], grad_fn=)
b的估计误差: tensor([0.0005], grad_fn=)

参数学习率过大、过小的实现

更改参数后，重新训练之前，需要把w、b初始化一次

lr=0.001 #学习率太小

结果：

epoch 1, loss 13.799065
epoch 2, loss 11.255581
epoch 3, loss 9.180990

可以看出损失变大了，解决办法：当学习率过小的话，可以增加扫描数据的次数，即增加更迭次数

lr = 0.001 #学习率
num_epochs = 20 #扫描数据次数

结果：

epoch 1, loss 13.728722
epoch 2, loss 11.198340
epoch 3, loss 9.134476
epoch 4, loss 7.451096
epoch 5, loss 6.078057
epoch 6, loss 4.958100
epoch 7, loss 4.044569
epoch 8, loss 3.299416
epoch 9, loss 2.691590
epoch 10, loss 2.195771
epoch 11, loss 1.791320
epoch 12, loss 1.461379
epoch 13, loss 1.192240
epoch 14, loss 0.972682
epoch 15, loss 0.793567
epoch 16, loss 0.647449
epoch 17, loss 0.528246
epoch 18, loss 0.430998
epoch 19, loss 0.351659
epoch 20, loss 0.286932

lr = 10 #学习率太大

结果：

epoch 1, loss nan
epoch 2, loss nan
epoch 3, loss nan

2 线性回归的简洁实现

通过使用深度学习框架来简洁地实现 线性回归模型 生成数据集

import numpy as np
import torch
from torch.utils import data #从torch.utils导入data的模具
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4]) #真实w
true_b = 4.2 #真实b
features, labels = d2l.synthetic_data(true_w, true_b, 1000) #通过函数生成特征和标号

调用框架中现有的API来读取数据

def load_array(data_arrays, batch_size, is_train=True):  
    """构造一个PyTorch数据迭代器。"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

next(iter(data_iter)) #通过next函数得到X和y,转成python的data_iter

结果：

[tensor([[ 0.2737, 1.0630],
[ 1.4066, -0.5917],
[ 1.7868, 1.0579],
[ 1.3324, 1.9590],
[ 0.8734, 0.1383],
[-0.3388, -0.7374],
[-0.3113, 0.8442],
[-1.6031, -1.8198],
[ 0.4201, 1.1438],
[ 0.1111, -0.5399]]),
tensor([[1.1285],
[9.0353],
[4.1812],
[0.2043],
[5.4785],
[6.0336],
[0.7109],
[7.1772],
[1.1677],
[6.2597]])]

使用框架的预定义好的层

#`nn`是神经网络的缩写
from torch import nn 

net = nn.Sequential(nn.Linear(2, 1)) #linear(2,1):输入输出维度；放进sequential容器里面

初始化模型参数

net[0].weight.data.normal_(0, 0.01) #权重w （normal_使用正态分布替换data值 均值为0 方差为0.01）
net[0].bias.data.fill_(0) #偏差b 设为0

计算均方误差使用的是MSELoss类，也称为平方 L2 范数

loss = nn.MSELoss()

实例化 SGD 实例

trainer = torch.optim.SGD(net.parameters(), lr=0.03) #传入的两个参数：parameters所有的参数、学习率

训练过程代码与我们从零开始实现时所做的非常相似

num_epochs = 3 #迭代三次数据
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X), y) #net自带模型参数w和b，所以这里不用写出来
        trainer.zero_grad() #梯度清零
        l.backward() #计算backward
        trainer.step() #调用step进行模型更新
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

结果：

epoch 1, loss 0.000314
epoch 2, loss 0.000100
epoch 3, loss 0.000101

比较生成数据集的真实参数和通过有限数据训练获得的模型参数

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

结果：

w的估计误差： tensor([0.0007, 0.0007])
b的估计误差： tensor([0.0003])