EM算法的仿真(三硬币+混合高斯)python 程序
1. 求解抛硬币的参数
(1)首先给出样本数据及说明
- 现在有A,B,C三个硬币,正面出现的概率分别为 π \pi π, p p p, q q q。
- 抛硬币的步骤:首先抛硬币A,硬币A正面朝上接下来抛硬币B,否则抛硬币C。
- 现在得到的样本数据为:
1,1,0,1,0,0,1,0,1,1。
(2)建立参数估计模型
- 假定未知的模型参数 θ = ( π , p , q ) \boldsymbol{\theta} = (\pi,p,q) θ=(π,p,q),每次抛掷硬币A(隐变量)的数据结果为 z z z,硬币B、C(观测变量)正反面的结果为 y y y。
P ( y ∣ θ ) = ∑ z P ( y , z ∣ θ ) = ∑ z P ( y ∣ z , θ ) P ( z ∣ θ ) = π p y ( 1 − p ) 1 − y + ( 1 − π ) q y ( 1 − q ) 1 − y \begin{aligned} P(y|\boldsymbol{\theta}) = \sum_z P(y,z|\boldsymbol{\theta}) = \sum_z P(y|z,\boldsymbol{\theta})P(z|\boldsymbol{\theta})\\ =\pi p^y(1-p)^{1-y} + (1-\pi)q^y(1-q)^{1-y} \end{aligned} P(y∣θ)=z∑P(y,z∣θ)=z∑P(y∣z,θ)P(z∣θ)=πpy(1−p)1−y+(1−π)qy(1−q)1−y - 假定观测数据 y = ( y 1 , y 2 , . . . , y n ) T \boldsymbol{y} = (y_1,y_2,...,y_n)^T y=(y1,y2,...,yn)T,观测次数为 n n n,则最大似然估计的公式为
θ = arg max θ log P ( y ∣ θ ) \boldsymbol{\theta} = \argmax_\boldsymbol{\theta}\log P(\boldsymbol{y}|\boldsymbol{\theta}) θ=θargmaxlogP(y∣θ)
其中 P ( y ∣ θ ) = ∏ i = 0 n [ π p y ( 1 − p ) 1 − y + ( 1 − π ) q y ( 1 − q ) 1 − y ] P(\boldsymbol{y}|\boldsymbol{\theta}) = \prod_{i=0}^n [\pi p^y(1-p)^{1-y} + (1-\pi)q^y(1-q)^{1-y}] P(y∣θ)=i=0∏n[πpy(1−p)1−y+(1−π)qy(1−q)1−y]
(3)采用EM的步骤
-
计算隐变量
假定此时估计的 θ ( i ) = ( π ( i ) , p ( i ) , q ( i ) ) \boldsymbol{\theta}^{(i)} = (\pi^{(i)},p^{(i)},q^{(i)}) θ(i)=(π(i),p(i),q(i))。观测数据来自B的概率为:
μ ( i + 1 ) = π ( i ) ( p ( i ) ) y i ( 1 − p ( i ) ) 1 − y i π ( i ) ( p ( i ) ) y i ( 1 − p ( i ) ) 1 − y i + ( 1 − π ( i ) ) ( q ( i ) ) y i ( 1 − q ( i ) ) 1 − y i \mu ^{(i+1)}=\frac{\pi^{(i)} (p^{(i)})^{y_i}\left( 1-p^{(i)} \right) ^{1-y_i}}{\pi^{(i)} (p^{(i)})^{y_i}\left( 1-p^{(i)} \right) ^{1-y_i}+(1-\pi^{(i)}) (q^{(i)})^{y_i}\left( 1-q^{(i)} \right) ^{1-y_i}} μ(i+1)=π(i)(p(i))yi(1−p(i))1−yi+(1−π(i))(q(i))yi(1−q(i))1−yiπ(i)(p(i))yi(1−p(i))1−yi
观测数据来自C的概率为:1 − μ ( i + 1 ) 1-\mu^{(i+1)} 1−μ(i+1)
-
此时对观测数据来自 B 的概率取平均值就可以得到参数 π ( i + 1 ) = 1 n ∑ j = 1 N μ j ( i + 1 ) \pi^{(i+1)} = \frac{1}{n}\sum_{j=1}^N{\mu _j^{(i+1)}} π(i+1)=n1j=1∑Nμj(i+1)
类似的可以得到
p ( i + 1 ) = ∑ j = 1 N μ j ( i + 1 ) y j ∑ j = 1 N μ j ( i + 1 ) q ( i + 1 ) = ∑ j = 1 N ( 1 − μ j ( i + 1 ) ) y j ∑ j = 1 N ( 1 − μ j ( i + 1 ) ) p^{(i+1)}=\frac{\sum\limits_{j=1}^N{\mu _j^{(i+1)}y_j}}{\sum\limits_{j=1}^N{\mu _j^{(i+1)}}}~~~~~~~~ q^{(i+1)}=\frac{\sum\limits_{j=1}^N{(1-\mu _j^{(i+1)})y_j}}{\sum\limits_{j=1}^N{(1-\mu _j^{(i+1)}})} p(i+1)=j=1∑Nμj(i+1)j=1∑Nμj(i+1)yj q(i+1)=j=1∑N(1−μj(i+1))j=1∑N(1−μj(i+1))yj -
这里面仿真的是对于不同的初值最终 EM 算法会收敛到不同的概率预测值
sample = [1,1,0,1,0,0,1,0,1,1]
times = 20 #设定迭代参数为 20次
mu = []
def coin_EM(pi,p,q):
pi_copy = pi
q_copy = q
p_copy = p
for i in range(times):
sum_p = 0
sum_q = 0
for flap in sample:
if flap == 0:
mu.append(pi*(1-p)/(pi*(1-p)+(1-pi)*(1-q)))
else:
mu.append(pi*p/(pi*p+(1-pi)*q))
sum_p = sum_p + pi*p/(pi*p+(1-pi)*q)
sum_q = sum_q + 1 - pi*p/(pi*p+(1-pi)*q)
pi = sum(mu)/len(sample)
p = sum_p/sum(mu)
q = sum_q/(len(sample) - sum(mu))
mu.clear()
print("给定的初值分别为:")
print("pi = {:.4f} , p = {:.4f} , q = {:.4f}".format(pi_copy,p_copy,q_copy))
print("迭代得到的终值分别为:")
print("pi = {:.4f} , p = {:.4f} , q = {:.4f}".format(pi,p,q))
def MLE(pi,p,q):
index_one = 0
index_zero = 0
for clap in sample:
if clap == 1:
index_one = index_one + 1
index_zero = len(sample) - index_one
proability = pow(pi * p + (1-pi) * q,index_one) \
* pow(pi * (1-p) + (1-pi) * (1-q),index_zero)
print("对这一组的最大似然结果为:{:.5f}".format(proability))
print("第一组:")
coin_EM(0.46,0.55,0.67)
MLE(0.46,0.55,0.67)
print("###############################################")
print("第二组:")
coin_EM(0.5,0.5,0.5)
MLE(0.5,0.5,0.5)
print("###############################################")
print("第三组:")
coin_EM(0.4,0.6,0.7)
MLE(0.4,0.6,0.7)
#结果
第一组:
给定的初值分别为:
pi = 0.4600 , p = 0.5500 , q = 0.6700
迭代得到的终值分别为:
pi = 0.4619 , p = 0.5346 , q = 0.6561
对这一组的最大似然结果为:0.00119
###############################################
第二组:
给定的初值分别为:
pi = 0.5000 , p = 0.5000 , q = 0.5000
迭代得到的终值分别为:
pi = 0.5000 , p = 0.6000 , q = 0.6000
对这一组的最大似然结果为:0.00098
###############################################
第三组:
给定的初值分别为:
pi = 0.4000 , p = 0.6000 , q = 0.7000
迭代得到的终值分别为:
pi = 0.4064 , p = 0.5368 , q = 0.6432
对这一组的最大似然结果为:0.00110
2. 求解混合高斯分布的参数
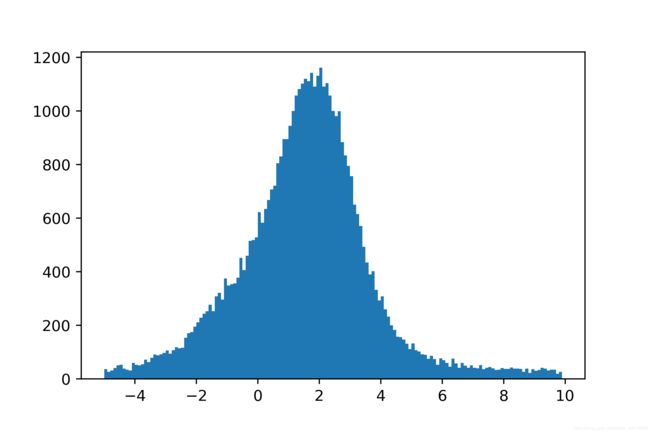
(1)首先生成并展示出混合高斯分布的数据
-
高斯混合模型的概率分布如下:
P ( y ∣ θ ) = ∑ k = 1 K α k ϕ ( y ∣ θ k ) P(y|\boldsymbol{\theta})=\sum_{k=1}^K\alpha_k\phi(y|\boldsymbol{\theta_k}) P(y∣θ)=k=1∑Kαkϕ(y∣θk)
参数为 θ = ( α 1 , α 2 , . . . , α k ; θ 1 , θ 2 , . . . , θ k ) \boldsymbol{\theta} = (\alpha_1,\alpha_2,...,\alpha_k;\boldsymbol{\theta_1},\boldsymbol{\theta_2},...,\boldsymbol{\theta_k}) θ=(α1,α2,...,αk;θ1,θ2,...,θk),且其中 α k \alpha_k αk 是系数(表示从各模型抽取的概率), ∑ k = 1 K α k = 1 , ϕ ( y ∣ θ k ) \displaystyle\sum_{k=1}^K\alpha_k =1,\phi(y|\boldsymbol{\theta_k}) k=1∑Kαk=1,ϕ(y∣θk) 是高斯分布密度, θ k = ( μ k , σ k 2 ) \boldsymbol{\theta_k}=(\mu_k,\sigma_k^2) θk=(μk,σk2),第 k k k 个分模型的概率密度函数是
ϕ ( y ∣ θ k ) = 1 2 π σ k exp ( − ( y − μ k ) 2 2 σ k 2 ) \phi(y|\boldsymbol{\theta_k}) = \displaystyle\frac{1}{\sqrt{2}\pi \sigma_k}\exp({-\frac{\left(y-\mu_k \right)^2}{2\sigma ^2_k}}) ϕ(y∣θk)=2πσk1exp(−2σk2(y−μk)2) -
假定样本是从三个一维高斯分布中抽取出来的,抽取的概率分别为:
p 1 = 1 2 , p 2 = 1 3 , p 3 = 1 6 p_1 = \frac{1}{2},p_2=\frac{1}{3},p_3 = \frac{1}{6} p1=21,p2=31,p3=61 -
这三个高斯函数的参数分别为:( μ 1 , σ 1 \mu_1,\sigma_1 μ1,σ1) = (1,2) , ( μ 2 , σ 2 \mu_2,\sigma_2 μ2,σ2) = (2,1),( μ 3 , σ 3 \mu_3,\sigma_3 μ3,σ3) = (4,8)
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
#下面完成50000次取样
times = 50000
choice = np.random.choice([1,2,3],size = (1,times),p = [1/2,1/3,1/6]).tolist()
sample_list = []
for i in choice[0]:
if i == 1:
sample_list.append(np.random.normal(1,2,1).item())
elif i == 2:
sample_list.append(np.random.normal(2,1,1).item())
else:
sample_list.append(np.random.normal(4,8,1).item())
sample_list = np.array(sample_list)
bins = np.arange(-5,10,0.1)
plt.hist(sample_list,bins)
plt.show()
(2)EM的理论算法流程
-
明确隐变量,写出完全数据的对数似然函数
观测数据 y 1 , y 2 , . . . , y N y_1,y_2,...,y_N y1,y2,...,yN,反映观测数据 y k y_k yk 来自第 k k k 个分模型的隐变量 γ j k \gamma_{jk} γjk
γ j k = { 1 , 第 j 个 观 测 变 量 来 自 第 k 个 分 模 型 0 , 其 余 情 况 \gamma_{jk} = \begin{cases} 1, & 第 j 个观测变量来自第 k 个分模型 \\ 0, & 其余情况 \end{cases} γjk={1,0,第j个观测变量来自第k个分模型其余情况
综合观测数据和未观测数据可以得到完全数据是 ( y j , γ j 1 , γ j 2 , . . . , γ j k ) (y_j,\gamma_{j1},\gamma_{j2},...,\gamma_{jk}) (yj,γj1,γj2,...,γjk)。
写出完全数据的似然函数
P ( y , γ ∣ θ ) = ∏ j = 1 N P ( y j , γ j 1 , γ j 2 , . . . , γ j K ∣ θ ) = ∏ k = 1 K ∏ j = 1 N ( α k ϕ ( y j ∣ θ k ) ) γ j k = ∏ k = 1 K α k n k ∏ j = 1 N [ ϕ ( y j ∣ θ k ) ] γ j k = ∏ k = 1 K α k n k ∏ j = 1 N [ 1 2 π σ k exp ( − ( y j − μ k ) 2 2 σ k 2 ) ] γ j k \begin{aligned} P(y,\boldsymbol{\gamma}|\boldsymbol{\theta}) &= \prod_{j=1}^NP(y_j,\gamma_{j1},\gamma_{j2},...,\gamma_{jK}|\boldsymbol{\theta})\\ &= \prod_{k=1}^K\prod_{j=1}^N(\alpha_k\phi(y_j|\boldsymbol{\theta_k}))^{\gamma_{jk}}\\ &=\prod_{k=1}^K\alpha_k^{n_k}\prod_{j=1}^N[\phi(y_j|\boldsymbol{\theta_k})]^{\gamma_{jk}}\\ &=\prod_{k=1}^K\alpha_k^{n_k}\prod_{j=1}^N[\displaystyle\frac{1}{\sqrt{2}\pi \sigma_k}\exp({-\frac{\left(y_j-\mu_k \right)^2}{2\sigma ^2_k})]^{\gamma_{jk}}} \end{aligned} P(y,γ∣θ)=j=1∏NP(yj,γj1,γj2,...,γjK∣θ)=k=1∏Kj=1∏N(αkϕ(yj∣θk))γjk=k=1∏Kαknkj=1∏N[ϕ(yj∣θk)]γjk=k=1∏Kαknkj=1∏N[2πσk1exp(−2σk2(yj−μk)2)]γjk
其中 n k = ∑ j = 1 N γ j k n_k = \displaystyle\sum_{j=1}^N\gamma_{jk} nk=j=1∑Nγjk, ∑ k = 1 K n k = N \displaystyle\sum_{k=1}^K n_k = N k=1∑Knk=N
变成对数形式 log P ( y , γ ∣ θ ) = ∑ k = 1 K n k log α k + ∑ j = 1 N γ j k [ log ( 1 2 π ) − log σ k − 1 2 σ k 2 ( y j − μ k ) 2 ] \log P(y,\gamma|\boldsymbol{\theta}) = \displaystyle\sum_{k=1}^K n_k\log\alpha_k+\sum_{j=1}^N\gamma_{jk}[\log(\frac{1}{\sqrt{2\pi}})-\log{\sigma_k}-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2] logP(y,γ∣θ)=k=1∑Knklogαk+j=1∑Nγjk[log(2π1)−logσk−2σk21(yj−μk)2] -
E步:确定 Q 函数
Q ( θ , θ ( i ) ) = E [ log P ( y , γ ∣ θ ) ] = ∑ k = 1 K n k log α k + ∑ j = 1 N γ ^ j k [ log ( 1 2 π ) − log σ k − 1 2 σ k 2 ( y j − μ k ) 2 ] \begin{aligned} Q(\theta,\theta^{(i)}) &= E[\log{P(y,\gamma|\boldsymbol{\theta})}]\\ &= \displaystyle\sum_{k=1}^K n_k\log\alpha_k+\sum_{j=1}^N\hat{\gamma}_{jk}[\log(\frac{1}{\sqrt{2\pi}})-\log{\sigma_k}-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2] \end{aligned} Q(θ,θ(i))=E[logP(y,γ∣θ)]=k=1∑Knklogαk+j=1∑Nγ^jk[log(2π1)−logσk−2σk21(yj−μk)2]
其中 γ ^ j k = α k ϕ ( y j ∣ θ k ) ∑ k = 1 K α k ϕ ( y j ∣ θ k ) ( j = 1 , 2 , . . , N ) ( k = 1 , 2 , . . . , K ) \hat{\gamma}_{jk}=\frac{\alpha_k\phi \left(y_j|\theta_k \right)}{\sum\limits_{k=1}^K{\alpha_k\phi \left(y_j|\theta_k \right)}}\left(j=1,2, ..,N \right)\left(k=1,2, ...,K \right) γ^jk=k=1∑Kαkϕ(yj∣θk)αkϕ(yj∣θk)(j=1,2,..,N)(k=1,2,...,K) -
M步:确定 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)
θ ( i + 1 ) = arg max θ Q ( θ , θ ( i ) ) \theta^{(i+1)} = \argmax_{\boldsymbol{\theta}}Q(\boldsymbol{\theta},\boldsymbol{\theta}^{(i)}) θ(i+1)=θargmaxQ(θ,θ(i))
通过求偏导可得
μ ^ k = ∑ j = 1 N γ ^ j k y j ∑ j = 1 N γ ^ j k σ ^ k 2 = ∑ j = 1 N γ ^ j k ( y j − μ k ) 2 ∑ j = 1 N γ ^ j k α ^ k = ∑ j = 1 N γ ^ j k N ( k = 1 , 2 , . . . , K ) \hat{\mu}_k=\frac{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}y_j}}{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}}}~~~~ \hat{\sigma}_{k}^{2}=\frac{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}\left( y_j-\mu_k \right) ^2}}{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}}}~~~~ \hat{\alpha}_k=\frac{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}}}{N}\left( k=1,2,...,K \right) μ^k=j=1∑Nγ^jkj=1∑Nγ^jkyj σ^k2=j=1∑Nγ^jkj=1∑Nγ^jk(yj−μk)2 α^k=Nj=1∑Nγ^jk(k=1,2,...,K)
(3)EM的编程算法流程
-
EM 的步骤:
输入:观测数据 y 1 , y 2 , . . . , y N y_1,y_2,...,y_N y1,y2,...,yN,高斯混合模型;
输出:高斯混合模型参数
-
取参数的初始值并开始迭代。
-
E步:依据当前模型参数,计算分模型 k k k对观测数据 y j y_j yj的响应度
γ ^ j k = α k ϕ ( y j ∣ θ k ) ∑ k = 1 K α k ϕ ( y j ∣ θ k ) ( j = 1 , 2 , . . , N ) ( k = 1 , 2 , . . . , K ) \hat{\gamma}_{jk}=\frac{\alpha_k\phi \left(y_j|\theta_k \right)}{\sum\limits_{k=1}^K{\alpha_k\phi \left(y_j|\theta_k \right)}}\left(j=1,2, ..,N \right)\left(k=1,2, ...,K \right) γ^jk=k=1∑Kαkϕ(yj∣θk)αkϕ(yj∣θk)(j=1,2,..,N)(k=1,2,...,K)
- M步:计算新一轮的迭代参数
μ ^ k = ∑ j = 1 N γ ^ j k y j ∑ j = 1 N γ ^ j k σ ^ k 2 = ∑ j = 1 N γ ^ j k ( y j − μ k ) 2 ∑ j = 1 N γ ^ j k α ^ k = ∑ j = 1 N γ ^ j k N ( k = 1 , 2 , . . . , K ) \hat{\mu}_k=\frac{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}y_j}}{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}}}~~~~ \hat{\sigma}_{k}^{2}=\frac{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}\left( y_j-\mu_k \right) ^2}}{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}}}~~~~ \hat{\alpha}_k=\frac{\sum\limits_{j=1}^N{\hat{\gamma}_{jk}}}{N}\left( k=1,2,...,K \right) μ^k=j=1∑Nγ^jkj=1∑Nγ^jkyj σ^k2=j=1∑Nγ^jkj=1∑Nγ^jk(yj−μk)2 α^k=Nj=1∑Nγ^jk(k=1,2,...,K)
(3)在这个例子中的EM
- 在这里总共有50000个样本,因此 N = 50000 N=50000 N=50000。总共有3个高斯分布,因此 K = 3 K=3 K=3。
- 给出初始迭代值
p 1 = 1 4 , p 2 = 1 2 , p 3 = 1 4 p_1 = \frac{1}{4},p_2=\frac{1}{2},p_3 = \frac{1}{4} p1=41,p2=21,p3=41
( μ 1 , σ 1 \mu_1,\sigma_1 μ1,σ1) = (1,1) , ( μ 2 , σ 2 \mu_2,\sigma_2 μ2,σ2) = (2,2), ( μ 3 , σ 3 \mu_3,\sigma_3 μ3,σ3) = (3,3) - 得到的迭代收敛值
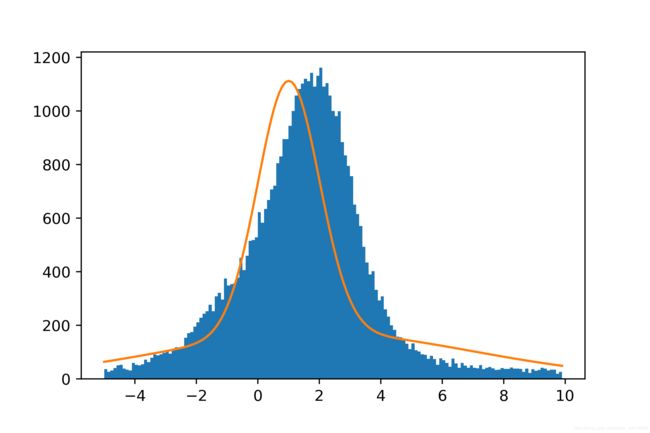
得到的概率值为: p 1 = 0.17 , p 2 = 0.35 , p 3 = 0.47 p_1 = 0.17,p_2 = 0.35,p_3 = 0.47 p1=0.17,p2=0.35,p3=0.47
得到的分布为:( μ 1 , σ 1 \mu_1,\sigma_1 μ1,σ1) = (1,1) , ( μ 2 , σ 2 \mu_2,\sigma_2 μ2,σ2) = (1,1), ( μ 3 , σ 3 \mu_3,\sigma_3 μ3,σ3) = (2,5)
import scipy.stats
gamma = np.empty([times,3])
p = np.array([1 / 4, 1 / 2, 1 / 4])
mu = np.array([1, 2, 3])
std = np.array([1, 2, 3])
#这里设定迭代次数为1000次
iteration = 1000
# 这里进行 E-step的操作
def E_step():
calculate_temp = np.empty((times,3))
for k in range(3):
calculate_temp[:, k] = p[k] * scipy.stats.norm(mu[k], std[k]).pdf(sample_list)
divide_temp = np.sum(calculate_temp, axis=1).reshape(times, )
for k in range(3):
gamma[:, k] = calculate_temp[:, k] / divide_temp
#这里进行M-step的操作
def M_step():
for k in range(3):
# 这里更新mu的值
mu[k] = np.divide(np.sum(gamma[:,k] * sample_list) ,np.sum(gamma[:,k]))
# 这里更新std的值
std[k] = np.sqrt(np.sum(gamma[:,k] * np.square(sample_list - mu[k]))/np.sum(gamma[:,k]))
# 这里更新p的值
p[k] = np.sum(gamma[:,k]) / times
for cnt in np.arange(iteration):
E_step()
M_step()
print("得到的概率值为:p1 = {:.2f},p2 = {:.2f},p3 = {:.2f}".format(p[0],p[1],p[2]))
print("得到的分布为:(mu1,std1) = ({},{}) (mu2,std2) = ({},{}) (mu3,std3) = ({},{})".format(mu[0],std[0],mu[1],std[1],mu[2],std[2]))
(4)画出EM计算出的结果
import math
EM_lis = np.arange(-5,10,0.1)
EM_draw = np.zeros(EM_lis.shape)
for j in range(3):
EM_draw = EM_draw + scipy.stats.norm(mu[j],std[j]).pdf(EM_lis)* p[j]
#下面乘以4500只是做一个scale,并没有其他的含义
plt.plot(EM_lis,EM_draw*4500)
plt.hist(sample_list,bins)
plt.show()