(人工智能的数学基础)第一章特征向量与矩阵分析——第三节:特征向量与特征值
参考
- 3Blue1Brown系列:特征向量和特征值
- 第十章 线性代数之 特征向量与特征值】3Blue1Brown
- 知乎:线性代数的本质10 特征向量和特征值
文章目录
- 一:特征向量与特征值概念引入
- 二:特征向量与特征值概念求解
- 三:特征向量与特征值概念注意
- 四:如果基向量就是特征向量(特征基)
- 五:特征向量与特征值应用举例-特征降维
一:特征向量与特征值概念引入
我们知道,基向量 i = ( 1 0 ) i=\begin{pmatrix} 1 \\ 0 \end{pmatrix} i=(10)和 j = ( 0 1 ) j=\begin{pmatrix} 0 \\ 1 \end{pmatrix} j=(01)会通过 ( 3 1 0 2 ) \begin{pmatrix} 3 & 1\\ 0 & 2\end{pmatrix} (3012)变换为 i = ( 3 0 ) i=\begin{pmatrix} 3 \\ 0 \end{pmatrix} i=(30)和 j = ( 1 2 ) j=\begin{pmatrix} 1 \\ 2 \end{pmatrix} j=(12),所以通过矩阵 ( 3 1 0 2 ) \begin{pmatrix} 3 & 1\\ 0 & 2\end{pmatrix} (3012)就可以描述这个变换
如下图,黄色向量张成的空间为粉色直线,在矩阵 ( 3 1 0 2 ) \begin{pmatrix} 3 & 1\\ 0 & 2\end{pmatrix} (3012)所描述的变化下、,黄色向量离开了它原来张成的空间,这是因为黄色向量既有缩放又有旋转变换
- 如果黄色向量只有缩放没有旋转,那么最终黄色向量会和粉色向量重合
如下图,由于黄色向量只经历了缩放而没有经历旋转,所以黄色向量仍然留在原来张成的空间上
特征向量和特征值:如果某向量经过线性变换后仍然停留在其变换前的张成空间中,则称此类向量为特征向量;而特征值指的就是该特征向量被拉伸或压缩时的比例因子。也即可以这样理解它们,一个向量 v v v在矩阵变换 A A A下得到了一个新的向量 A v Av Av,该向量等于将原来的向量 v v v缩放 λ \lambda λ倍,即
A v = λ v Av=\lambda v Av=λv
特征向量和特征值描述了这样一个事实:我们知道,变换矩阵会对原向量进行旋转和缩放然后得到新向量。此时,如果得出的新向量与原向量方向相同,只是在大小上存在区别,则称变化前的向量为变换矩阵的特征向量,同时,变化矩阵只对原向量进行缩放操作,旋转角度为0。变换前后矩阵特征向量的缩放比例称为该变换矩阵的特征值
假设特征值为1,特征向量为 v v v,则有 A v = 1 ⋅ v Av=1 \cdot v Av=1⋅v
假设特征值为 − 1 2 -\frac{1}{2} −21,特征向量为 v v v,则有 A v = − 1 2 ⋅ v Av=-\frac{1}{2} \cdot v Av=−21⋅v
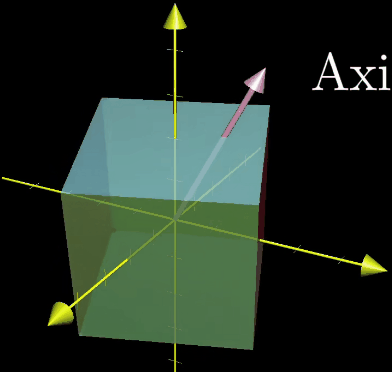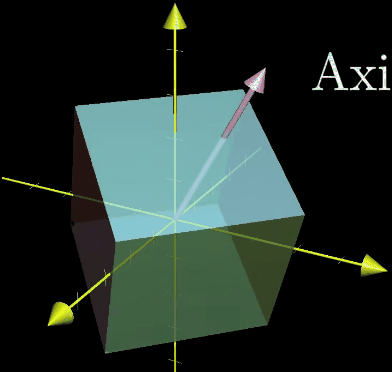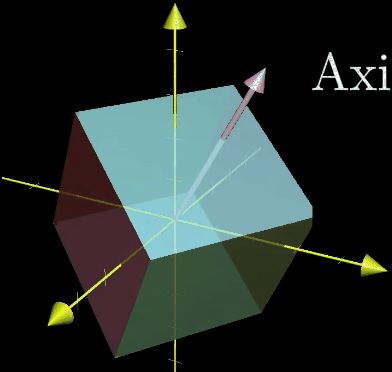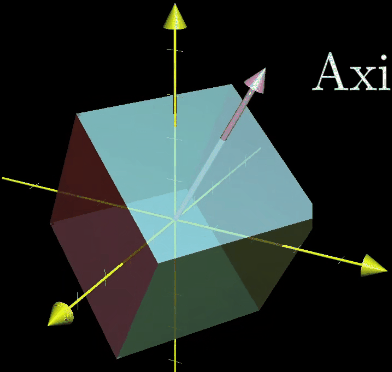
如果考虑一个三维空间中的旋转变化,该变化的特征向量就是旋转轴,在这种旋转变化中,特征值为1,因为空间只发生旋转而不会有拉伸和压缩
二:特征向量与特征值概念求解
对于下面的定义式,现在等式两边类型不统一
A v = λ v Av=\lambda v Av=λv
在等式右面加入单位矩阵 I I I,使其也变为“矩阵乘向量”的形式
A v = ( λ I ) v Av=(\lambda I)v Av=(λI)v
移动到左面
A v − ( λ I ) v = 0 Av-(\lambda I)v=0 Av−(λI)v=0
将 v v v提出来之后,此式就可以看作向量 v v v在矩阵 ( A − λ I ) (A- \lambda I) (A−λI)的作用下变成了零向量
( A − λ I ) v = 0 (A-\lambda I)v=0 (A−λI)v=0
这说明这个矩阵具有压缩向量的作用,可以将非零向量压缩为零向量。所以我们需要一个非零解 v v v,使得矩阵和它的乘积为零向量,而空间压缩其本质就是矩阵行列式为零,也即
d e t ( A − λ I ) = 0 det(A-\lambda I)=0 det(A−λI)=0
例如下图,当 λ \lambda λ改变时,矩阵也在改变,行列式的值同样在改变
当 λ = 1 \lambda=1 λ=1时,空间被压缩到低维度上(即行列式为0)
三:特征向量与特征值概念注意
1:二维线性变换不一定都有特征向量
如下图,黄色向量经过矩阵作用后并没有停留在原来张成的空间中
并且通过运算也可得知,它没有实数解
2:同一个特征值可能对应多个特征向量,这几个特征向量可能不在一条直线上
如下图,利用一个矩阵将所有向量都变为两倍,此时存在唯一特征值是2,但是平面内每一个向量都是属于这个特征值的特征向量
四:如果基向量就是特征向量(特征基)
如果所有基向量都是特征向量,那么此时矩阵的对角元就是他们所属的特征值,该矩阵为对角阵
五:特征向量与特征值应用举例-特征降维
特征向量与特征值的一个典型应用就是特征降维,其核心思想是在尽可能少地影响待观测对象特征向量可分离性的前提下,尽可能多地减少表达该对象属性特征的向量维度
例如经典的特征降维方法主成分分析(PCA),会将所有原特征向量分别向变化矩阵对应特征值较大的特征向量方向投影,这里的变化矩阵是指协方差矩阵