图的两种遍历:深度优先遍历+广度优先遍历
一、深度优先遍历
1、简介
深度优先遍历是指按照深度方向搜索,它类似于树的先根遍历,是树的先根遍历的推广。
基本思想(通俗)
选一条路走到 底,直到 走不通,就 原路返回看看 是否还有路可走,如果返回到起点还无路可走,说明深度优先遍历已完成。
2、举例说明
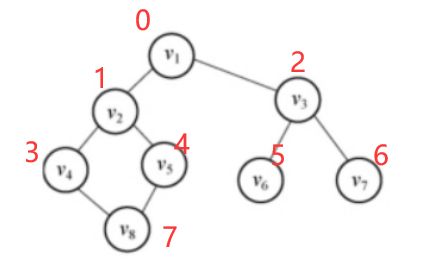
这是要深度遍历的无向图:
深度遍历依次访问的点为:
v1->v2->v4->v8->v5->v3->v6->v7
3、C语言代码
(1)邻接矩阵存储无向图。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
对于图的存储,请参考我的文章:图的三种存储结构:邻接矩阵表示法+链表法+十字链表法
存储无向图
#include
#include
#define MAX_VERTEM_NUM 10
#define INFINITY 32768
typedef enum{
DG,DN,UDG,UDN
}graghKind;
//digraph DG有向图
//directed network DN有向网
//undirected graph UDG无向图
//undirected network UDN无向网
typedef char vertemData;
typedef struct {
vertemData vert[MAX_VERTEM_NUM]; //顶点向量
int adj[MAX_VERTEM_NUM][MAX_VERTEM_NUM]; //邻接矩阵
int vertNum,arcNum; //图的顶点数和弧数
graghKind gragh; //图的类型
}adjMatrix;
//求顶点位置
int locateVertem(adjMatrix *G,vertemData v){
for(int j=0;jvertNum;j++)
{
if(G->vert[j]==v)
{
return j;
}
}
}
//创建无向图
int creatUDG(adjMatrix *G){
int i,j,k,weight;
vertemData v1,v2;
printf("请输入图的顶点数和弧数:\n");
scanf("%d %d",&G->vertNum,&G->arcNum);
for(i=0;ivertNum;i++)
for(j=0;jvertNum;j++)
G->adj[i][j] = 0;
for(i=0;ivertNum;i++)
{
printf("请输入图的顶点%d:\n",i);
getchar();
scanf("%c",&G->vert[i]);
}
for(k=0;karcNum;k++){
printf("请输入弧%d的两个顶点:\n",k);
getchar();
scanf("%c %c",&v1,&v2);
i = locateVertem(G,v1);
j = locateVertem(G,v2);
G->adj[i][j] = 1;
G->adj[j][i] = 1;
}
printf("\n无向图存储完毕!\n\n");
return 0;
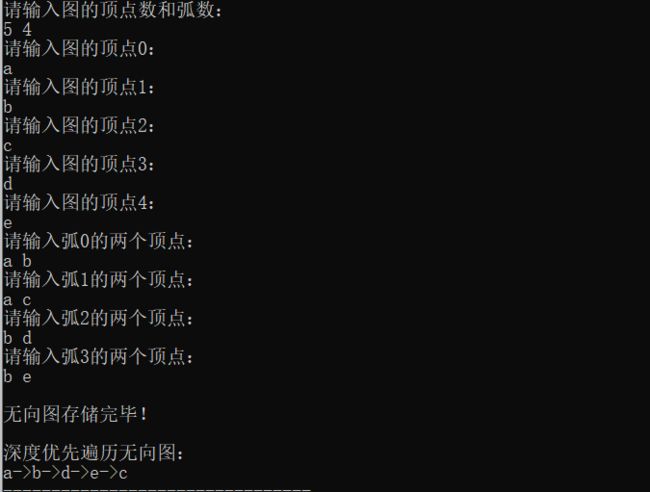
} 运行结果
(2) 用一个数组去存储已访问点的信息
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0代表该点未访问,1代表该点访问了。
(3)深度遍历的算法描述
- 更新访问点数组信息,在邻接矩阵当中找到该访问点的最近的邻接点,访问该邻接点,输出遍历顶点信息,重复此步骤。
- 当无法继续深度遍历的时候,在访问点数组中往后依次退1,直到能有一个顶点能继续深度遍历。
- 当起点都无法继续深度遍历的时候,对图的深度遍历已完成
实际就是从第n个顶点开始、标记该顶点已被访问,然后查找该顶点第一个未访问的邻接点第i个顶点,再去第i个顶点 深度遍历。
实际就是一个递归的过程。
//深度遍历无向图
void depth_first_traversal_UDG(adjMatrix *G,int *v,int n)
{
int i;
if(G==NULL) return;
if(n<0||n>G->vertNum) return;
v[n] = 1;
if(n==0) printf("%c",G->vert[n]);
else printf("->%c",G->vert[n]);
for(i=0;ivertNum;i++)
if(G->adj[n][i]!=0&&v[i]!=1) depth_first_traversal_UDG(G,v,i);
} (4)完整代码
#include
#include
#define MAX_VERTEM_NUM 10
#define INFINITY 32768
typedef enum{
DG,DN,UDG,UDN
}graghKind;
//digraph DG有向图
//directed network DN有向网
//undirected graph UDG无向图
//undirected network UDN无向网
typedef char vertemData;
typedef struct {
vertemData vert[MAX_VERTEM_NUM]; //顶点向量
int adj[MAX_VERTEM_NUM][MAX_VERTEM_NUM]; //邻接矩阵
int vertNum,arcNum; //图的顶点数和弧数
graghKind gragh; //图的类型
}adjMatrix;
//求顶点位置
int locateVertem(adjMatrix *G,vertemData v){
for(int j=0;jvertNum;j++)
{
if(G->vert[j]==v)
{
return j;
}
}
}
//创建无向图
int creatUDG(adjMatrix *G){
int i,j,k,weight;
vertemData v1,v2;
printf("请输入图的顶点数和弧数:\n");
scanf("%d %d",&G->vertNum,&G->arcNum);
for(i=0;ivertNum;i++)
for(j=0;jvertNum;j++)
G->adj[i][j] = 0;
for(i=0;ivertNum;i++)
{
printf("请输入图的顶点%d:\n",i);
getchar();
scanf("%c",&G->vert[i]);
}
for(k=0;karcNum;k++){
printf("请输入弧%d的两个顶点:\n",k);
getchar();
scanf("%c %c",&v1,&v2);
i = locateVertem(G,v1);
j = locateVertem(G,v2);
G->adj[i][j] = 1;
G->adj[j][i] = 1;
}
printf("\n无向图存储完毕!\n\n");
return 0;
}
//深度遍历无向图
void depth_first_traversal_UDG(adjMatrix *G,int *v,int n)
{
int i;
if(G==NULL) return;
if(n<0||n>G->vertNum) return;
v[n] = 1;
if(n==0) printf("%c",G->vert[n]);
else printf("->%c",G->vert[n]);
for(i=0;ivertNum;i++)
if(G->adj[n][i]!=0&&v[i]!=1) depth_first_traversal_UDG(G,v,i);
}
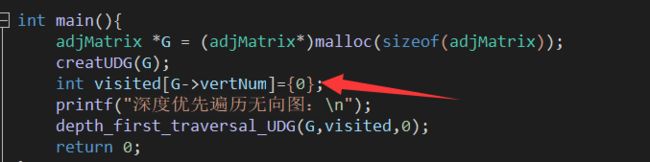
int main(){
adjMatrix *G = (adjMatrix*)malloc(sizeof(adjMatrix));
creatUDG(G);
int visited[G->vertNum]={0};
printf("深度优先遍历无向图:\n");
depth_first_traversal_UDG(G,visited,0);
return 0;
} 运行结果
附
二、广度优先遍历
1、简介
广度优先搜索是指按照广度方向搜索,它类似于树的按层次遍历,是树的按层次遍历的推广。
基本思想(通俗)
把一层的邻接点访问完后再去访问下一层。
2、举例说明
这是要广度遍历的无向图:
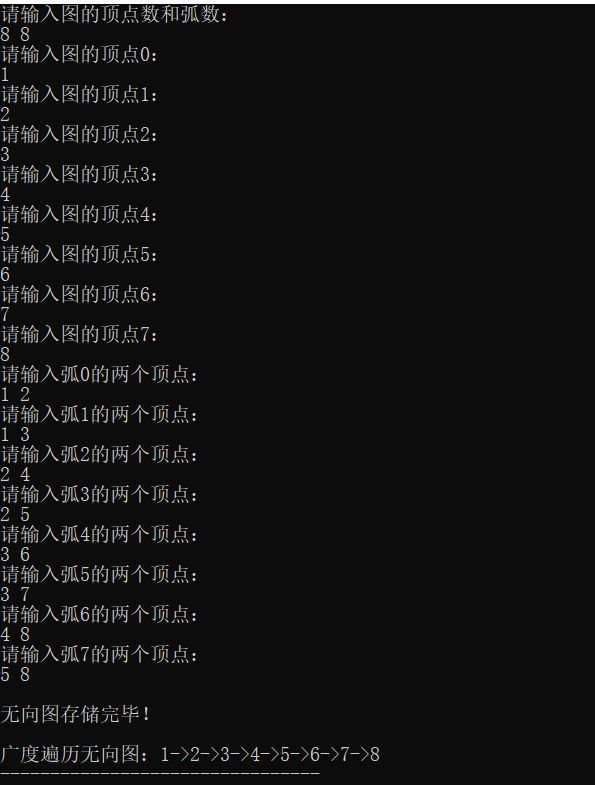
对无向图进行广度优先遍历:
v1->v2->v3->v4->v5->v6->v7->v8
3、C语言代码
(1)算法描述
当访问到n层的时候,依次入队列,出队列的顶点访问其邻接点并入队列。
广度遍历上图的情况下队列的变化如下:
1
2 3
3 4 5
4 5 6 7
5 6 7 8
6 7 8
7 8
8(2)完整代码
#include
#include
#define MAX_VERTEM_NUM 10
typedef enum{
DG,DN,UDG,UDN
}graghKind;
//digraph DG有向图
//directed network DN有向网
//undirected graph UDG无向图
//undirected network UDN无向网
typedef char vertemData;
int visited[MAX_VERTEM_NUM] = {0};//访问数组
/*邻接矩阵*/
typedef struct {
vertemData vert[MAX_VERTEM_NUM]; //顶点向量
int adj[MAX_VERTEM_NUM][MAX_VERTEM_NUM]; //邻接矩阵
int vertNum,arcNum; //图的顶点数和弧数
graghKind gragh; //图的类型
}adjMatrix;
/*队列结构*/
typedef struct QNode
{
vertemData data;
struct QNode *next;
}QNode;
typedef struct
{
QNode *front,*rear; //队头队尾指针
}LinkQueue;
/*求顶点位置*/
int locateVertem(adjMatrix *G,vertemData v){
for(int j=0;jvertNum;j++)
{
if(G->vert[j]==v)
{
return j;
}
}
}
/*创建无向图*/
int creatUDG(adjMatrix *G){
int i,j,k,weight;
vertemData v1,v2;
printf("请输入图的顶点数和弧数:\n");
scanf("%d %d",&G->vertNum,&G->arcNum);
for(i=0;ivertNum;i++)
for(j=0;jvertNum;j++)
G->adj[i][j] = 0;
for(i=0;ivertNum;i++)
{
printf("请输入图的顶点%d:\n",i);
getchar();
scanf("%c",&G->vert[i]);
}
for(k=0;karcNum;k++){
printf("请输入弧%d的两个顶点:\n",k);
getchar();
scanf("%c %c",&v1,&v2);
i = locateVertem(G,v1);
j = locateVertem(G,v2);
G->adj[i][j] = 1;
G->adj[j][i] = 1;
}
printf("\n无向图存储完毕!\n\n");
return 0;
}
/*创建空队列*/
int init_queue(LinkQueue *L)
{
L->front=L->rear=(QNode*)malloc(sizeof(QNode));
if(!L->front) return 0;
L->front->next=NULL;
return 0;
}
/*判断队列是否为空*/
int empty_queue(LinkQueue *L)
{
if(L->front->next==NULL) return 1;
else return 0;
}
/*入队列*/
int in_queue(LinkQueue *L,int n)
{
QNode *t = (QNode*)malloc(sizeof(QNode));
if(!t) exit(0);
t->data = n;
t->next = NULL;
L->rear->next = t;
L->rear = t;
free(t);
return 0;
}
/*出队列*/
int out_queue(LinkQueue *L)
{
QNode *t;
if(L->front==L->rear) return 0;
t = L->front->next;
L->front->next = t->next;
if(t==L->rear) L->rear = L->front;
return 1;
}
/*广度遍历*/
int BFS_traverse_UDN(adjMatrix *G)
{
int i=0,j;
LinkQueue *L = (LinkQueue*)malloc(sizeof(LinkQueue));
init_queue(L);
printf("广度遍历无向图:");
visited[i] = 1;
printf("%c",G->vert[i]);
in_queue(L,i);
do
{
out_queue(L);
for(j=0;jvertNum;j++)
{
if(G->adj[i][j]!=0&&visited[j]!=1)
{
visited[j] = 1;
printf("->%c",G->vert[j]);
in_queue(L,j);
}
}
i++;
}while(!empty_queue(L));
free(L);
return 0;
}
int main()
{
adjMatrix *G = (adjMatrix*)malloc(sizeof(adjMatrix));
creatUDG(G);
BFS_traverse_UDN(G);
return 0;
}
附