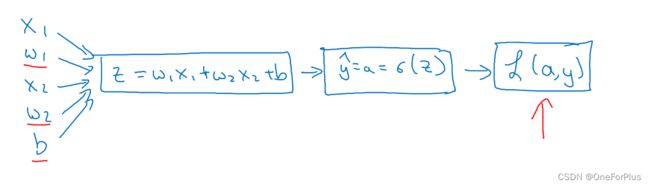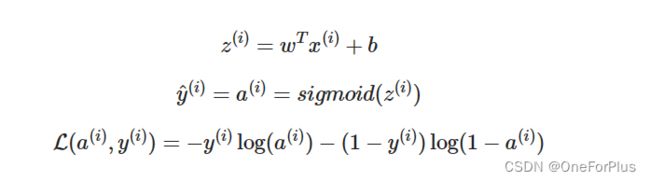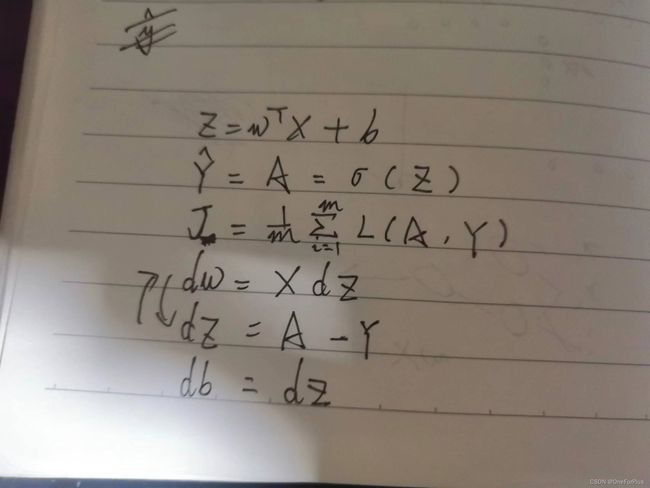deepLearning-Logistic Regression 逻辑回归单元
一直是跟着cousera上吴恩达的课学下来的，目前到一课程第四周，还没做第四周作业。
除了明显为个人手写并用手机拍摄，以下提供的图片都来自吴恩达老师课件的截图
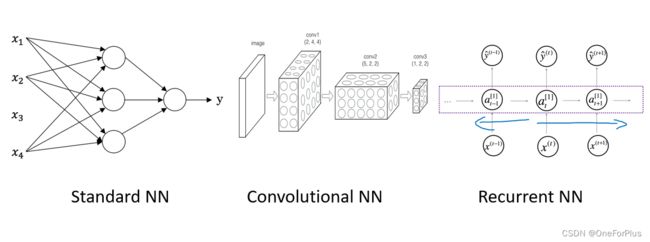
neural network 神经网络
在后期第四周的课里说明了这个和人脑神经元是没有可对比性的，也就是两者是完全没关系的东西。
这里给出个人理解的定义：神经网络就是由输入，多个层级的隐藏层，输出组成的预测模型。可以通过一个训练组进行训练，测试组进行测试。
对神经网络的理解可以参考电路中逻辑的实现，像是异或等的实现。
吴恩达老师课程里的一组关于神经网络的图片
Logistic Regression 逻辑回归单元
逻辑回归单元：实际就是神经网络中的一个节点，在前期课程中，这个节点通常是以神经网络中的输出节点为例的。
向前传播：根据输入+等式一直往后推到结果。这实际就是后来更新参数后要做的一个步骤，求得预测结果。
向后传播：根据结果+等式一直往前推到开头，实际就是求得个参数对结果的导数，知道参数对结果的影响大小。
单个样本时
涉及到的公式
当只有一个样本时，也就是上述 x ( i ) x^{(i)} x(i)时， x x x维度为 ( n , 1 ) (n,1) (n,1)
而在逻辑回归单元也只涉及到一个节点的计算，故此时 w w w维度应为 ( n , 1 ) (n,1) (n,1),故转置矩阵 w T w^{T} wT维度为 ( 1 , n ) (1,n) (1,n)
此时， z z z以及 y ^ \hat{y} y^的维度将是 ( 1 , 1 ) (1,1) (1,1)也就是我们想要的唯一的结果，但应注意到此时可能还需要对 y ^ \hat{y} y^进行处理才能是我们要的预测值。比如：判断一张图片是不是猫的时候， y ^ \hat{y} y^的结果可能会是 0.66 0.66 0.66等的小数，此时就需要键入判断条件，让结果转化为 0 0 0， 1 1 1来判断图片是不是猫。
损失函数 L ( a ( i ) , y ( i ) ) L( a^{(i)} , y^{(i)} ) L(a(i),y(i))对应到单个样本的误差，实际打代码时，其并没有显式地出现，而是作为成本函数的一部分加以运用。成本函数 c o s t ( A , Y ) cost( A, Y ) cost(A,Y)对应到多个样本的误差的平均值，实际就是运用这个函数来向前传播。
c o s t cost cost函数如下：
单个样本时，由损失函数向前传播得出的的导数如下：
其含义是对应参数对损失函数的求导
多个样本时
为了尽量避免在算法中出现 f o r for for循环拖慢运行速度，此时尽量将各种数据向量化，此时这里是对样本也就是 x x x的向量化，后续还有对 w w w也就是多节点时候的向量化，按照课程的说法，加入样本时按列加入，也就是一个样本占一列，比如样本维度为 ( n , m ) (n,m) (n,m)则说明存在 m m m个样本，由 n n n个数据唯一表示样本， w w w同理。
那么此时的各公式可归纳为如下：
说明：
1. X X X此时是 ( n , m ) ( n , m ) (n,m)维， w T w^{T} wT是 ( 1 , n ) (1 , n) (1,n)维，结果 z z z此时则是 ( 1 , m ) (1 , m) (1,m)维
2.激活函数在输出节点的选择上可以选择 s i g m o d ( ) sigmod() sigmod()函数此时选择的就是它。而它并不会改变输入的维度，因此 Y ^ \hat{Y} Y^维度为 ( 1 , m ) (1 , m) (1,m)刚好对应到 m m m个样本的预测判断结果。
3.对此时 c o s t cost cost函数的我的理解是，每个样本对应一个lose结果，此时算出来的 L ( A , Y ) L(A ,Y) L(A,Y)应当是一个 ( 1 , m ) (1 , m) (1,m)维的结果，而后累加，再除以样本数，就是 c o s t cost cost结果了。
4.下面的导数就没特意去理解其维数关系了，只需要跟着之前推导出来的公式去打代码就可以了。
逻辑回归单元的更新
通过train集训练逻辑回归单元，而后用test集测试训练后的逻辑回归单元的效果如何。
因为整个单元的目的就是算出合适的 w w w, b b b来组成 z = w ∗ X + b z=w*X+b z=w∗X+b，然后当 X X X，也就是待预测数据传入时能得出一个合适的结果。所以整一个是围绕算出合适的 w w w和 b b b进行的。因此，我们要做到的就是不断更新 w w w, b b b使 c o s t cost cost结果最小，也就是最趋近于真实的结果。
更新公式：
α \alpha α其含义是更新速率。合适的更新速率能较快获得较合适的 w w w, b b b，其偏大可能会直接错过 w w w, b b b,偏小则会导致更新较慢，所以在通常要通过多次实验获得合适的 α \alpha α。
w = w − α ⋅ d w w=w-\alpha\cdot dw w=w−α⋅dw
b = b − α ⋅ d b b=b-\alpha\cdot db b=b−α⋅db
实现逻辑回归单元
1.初始化 w w w, b b b
2.根据测试数据集(包含： X X X, Y Y Y,即有辨认数据，也有辨认结果数据)，算出 A A A, d w dw dw, d b db db, c o s t cost cost.
3.循环num_iterations次数更新 A A A, w w w, b b b, d w dw dw, d b db db, c o s t cost cost。 c o s t cost cost在这里是为了后期验证 w w w, b b b的有效性，或者说可视化更新过程的一个东西。
4.得出最后的w,b,也就是获得一个训练后的逻辑回归单元。
5.可以输入测试数据集测试回归单元的有效性了。
注意事项
1.num_iterations并不是越大越好，它越大最后出来的 w w w, b b b则越只能契合训练数据集，也就是说它对测试数据级的辨别能力会变弱。术语大概为：过度契合。
2.没有显式去求得的影响 w w w, b b b质量的参数，也称为超参数，有num_iterations, α \alpha α后续可能还有其他，这里只是想起来提一下。
3.不要混淆了 x ( 1 ) x^{(1)} x(1)和 x 1 x_1 x1的区别，一个是一个样本，一个是一个样本里的一个数据。
以上为个人观点，如有不当之处请批评指正