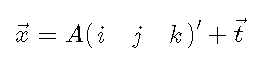3Dslicer医学图像三维坐标系(xyz,RAS,IJK)差异，转换，旋转，平面角
目录
World coordinate system世界坐标系xyz
Anatomical coordinate system解剖学坐标系(LPS/RAS/RAI)
Image coordinate system图像坐标系ijk
Image transformation图像转换
三维坐标变换
A.旋转矩阵和旋转向量
B.欧拉角
C.四元数编辑
计算平面角Angle Planes插件
参考链接
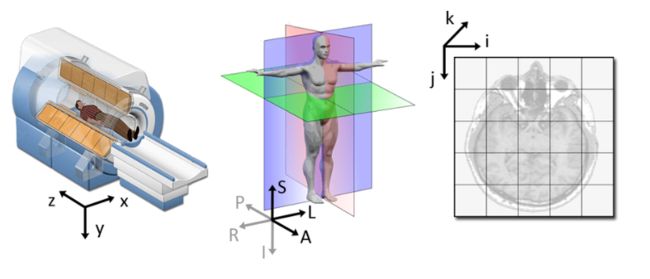
处理医学图像和应用程序时的问题之一是坐标系之间的差异。成像应用中常用三种坐标系：
xyz是世界坐标系
RAS是解剖坐标系，单位mm
IJK是像素/体素坐标系，单位像素pixel/体素voxel
世界（xyz轴） 解剖学（RAS轴） 图像坐标系（IJK轴）
每个坐标系都有一个用途，并以不同的方式表示其数据。
World coordinate system世界坐标系xyz
世界坐标系通常是一个笛卡尔坐标系，其中定位了模型（例如MRI扫描仪或患者）。每个模型都有自己的坐标系，但只有一个世界坐标系来定义每个模型的位置和方向。
Anatomical coordinate system解剖学坐标系(LPS/RAS/RAI)
医学成像技术最重要的模型坐标系是解剖空间（也称为患者坐标系）。这个空间由三个平面组成，用于描述人类的标准解剖位置：
- axial 平面平行于地面，将上与下分开
- coronal 平面垂直于地面，将前与后分开
- sagittal平面将左与右分开
从这些平面可以看出，所有轴的符号都在正方向上（例如，负上轴由下轴表示）。
解剖学坐标系是一个连续的三维空间，其中对图像进行了采样。在神经影像学中，通常根据正在扫描其大脑的人来定义这个空间。因此，3D基是沿着前后，下上和左右的解剖轴定义的。
然而，不同的医疗应用使用这种3D基础的不同定义。最常见的是以下基础：
- LPS（左、后、上）用于 DICOM 映像和 ITK 工具包
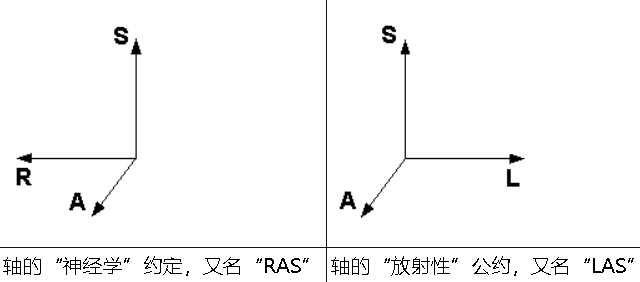
- RAS（右，前，上）类似于LPS，前两个轴翻转并由3D切片器使用
- LPS(Left, Posterior, Superior): MHD图像(meta image), ITK工具包, ITK-Snap软件(该软件中写的是RAI)使用
- RAS(Right, Anterior, Superior): Nifti图像和3D Slicer软件使用
注意以上两种均为右手坐标系. 其他的选择(如: RPI)和左手坐标系(如: LAS)也是可能遇到的, 需要注意区分.
警告: 人们并不总是用三个连续的字母表示正方向, 有时候也表示出发(from)的方向(也就是负方向), 此时上面的LPS会被写成RAI, 对应的到达(to)方向才是LPS. 比如ITK-Snap软件中Tools->Image Information->Orientation就写的是RAI, 表达的意思是 from RAI --> to LPS , 同样的使用 ITK 导出的MHD格式图像也是使用From模式.
这两个基础同样有用且合乎逻辑。只需要知道图像被引用到哪个基础。
Image coordinate system图像坐标系ijk
图像坐标系描述了如何获取相对于解剖结构的图像。医疗扫描仪创建从左上角开始的点和细胞的常规矩形阵列。i 轴向右增大，j 轴向右增大，k 轴向后增大。
除了每个体素的强度值（i j k）之外，还存储解剖坐标的原点和间距。
- 原点origin表示第一个体素 voxel（0，0，0） 在解剖坐标系中的位置，例如 （100mm， 50mm， -25mm）
- 间距spacing指定沿每个轴的体素之间的距离，例如（1.5mm，0.5mm，0.5mm）
以下 2D 示例显示了原点和间距的含义：
使用原点和间距，可以计算出每个（图像坐标）体素在解剖坐标中的相应位置。
Image transformation图像转换
从图像空间向量的变换(ijk)′到解剖空间向量x是仿射变换，线性变换A
转换矩阵A是一个3×3矩阵，并包含有关空间方向和轴缩放的所有信息。
t是一个3×1向量，并包含有关第一个体素的几何位置的信息。
最后一个方程表明线性变换是通过矩阵乘法和向量加法平移来执行的。为了表示转换和平移，必须使用矩阵乘法来表示增强矩阵。此技术要求矩阵一个在底部增加了一行额外的零，在右侧增加了一列（translation vector），在右下角增加了一个“1”。此外，所有向量都必须写成齐次坐标，这意味着“1”在最后被增强。
根据所使用的解剖空间（LPS 或 RAS）的不同，4×4矩阵称为 IJK 到线性函数矩阵或 IJK 拓扑矩阵，因为它表示从 IJK 到 LPS 或 RAS 的转换
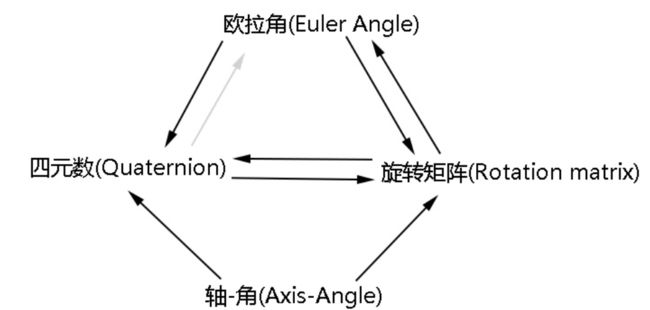
三维坐标变换
A.旋转矩阵和旋转向量
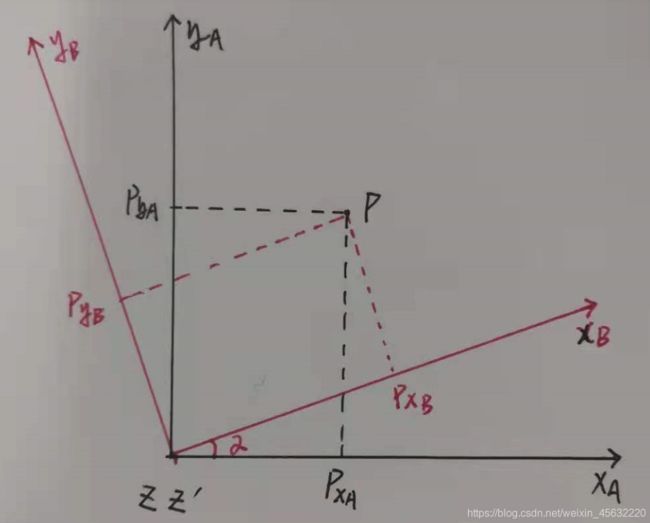
a坐标变换
b旋转向量
在3D图形学中，最常用的旋转表示方法便是四元数和欧拉角，比起矩阵来具有节省存储空间和方便插值的优点。
B.欧拉角
定义
，
，
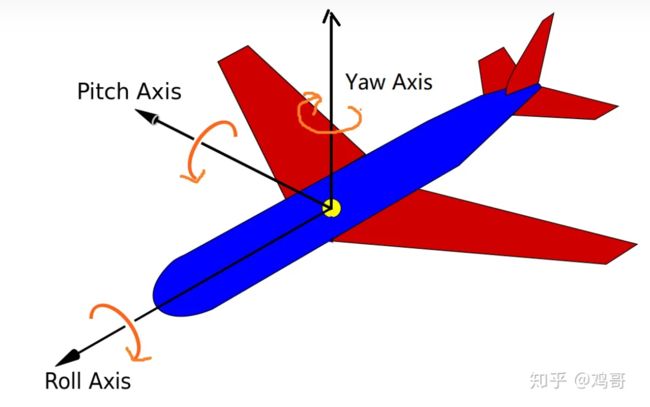
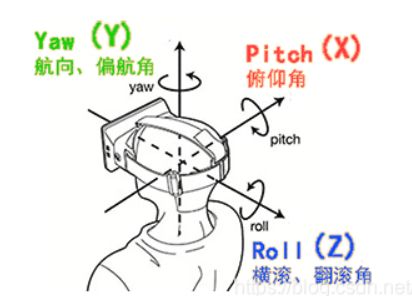
分别为绕Z轴、Y轴、X轴的旋转角度，如果用Tait-Bryan angle表示，分别为Yaw、Pitch、Roll。
(1) 欧拉角的表示方式不唯一。给定某个起始朝向和目标朝向，即使给定yaw、pitch、roll的顺序，也可以通过不同的yaw/pitch/roll的角度组合来表示所需的旋转。比如，同样的yaw-pitch-roll顺序，(0,90,0)和(90,90,90)会将刚体转到相同的位置。这其实主要是由于万向锁(Gimbal Lock)引起的 (2) 欧拉角的插值比较难。
(3) 计算旋转变换时，一般需要转换成旋转矩阵，这时候需要计算很多sin, cos，计算量较大。
C.四元数
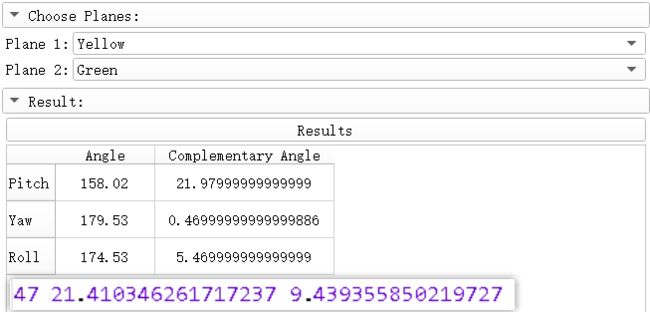
计算平面角Angle Planes插件
下载Angle Planes插件
此模块用于使用法线计算两个平面之间的角度。用户可以选择使用已在Slicer上实现的两个平面，也可以使用地标(至少3个地标)定义一个平面。也可以保存平面，以便在其他模型中重复使用。
Pitch Angle，complementary angle补角
右手系xyz顺规(分别对应roll, pitch,yaw)
参考链接
方向和体素顺序术语：RAS、激光、低密度聚乙烯、资源说明书、XYZ和所有这一切 (grahamwideman.com)
坐标系 - 切片器维基 (slicer.org)
slicer软件中RAS转换为像素坐标方法
旋转矩阵及左右乘的意义，看这一篇就够了_默以成之的博客-CSDN博客_旋转矩阵左乘和右乘的区别
四元数与欧拉角（Yaw、Pitch、Roll）的转换_xiaoma_bk的博客-CSDN博客_四元数转欧拉角医学影像简介(Medical Imaging Guide) (jarvis73.com)
三维旋转：欧拉角、四元数、旋转矩阵、轴角之间的转换 - 知乎pitch、yaw、roll三个角的区别_道道道人间道的博客-CSDN博客_yaw