Halcon 点云拟合平面并获取单位法向量及位姿
确实因为halcon的文档写的太好了,所以网上关于halcon的博客就很少,点云拟合平面的文档上介绍的比较详细,但是如何从平面模型中读取法向量可确实是难到了,找了三个小时人傻了,然后发现还是一行函数。
首先来说三维点云拟合平面,首先gen_object_model_3d_from_points,把点云转化为3d模型,输入:X,Y,Z坐标,输出ObjectModel3D
gen_object_model_3d_from_points( : : X, Y, Z : ObjectModel3D)
再选择拟合成想要的平面,使用fit_primitives_object_model_3d 把该上模型转化到Plane
fit_primitives_object_model_3d( : : ObjectModel3D, ParamName, ParamValue : ObjectModel3DOut)
ObjectModel3D:输入模型
ParamName:选择'primitive_type':拟合的类型,'fitting_algorithm':拟合方法等等
ParamValue:对应'primitive_type'------'cylinder', 'sphere', 'plane',就是"圆柱体","球体","平面"。对应'primitive_type'------'least_squares', 'least_squares_huber', 'least_squares_tukey'几种最小二乘法,这里选择plane和least_squares
ObjectModel3DOut:输出的平面
得到平面之后,ObjectModel3DOut相当于一个平面的模型,他里边包含各种平面的参数:pose,nomals等等,需要使用一个函数get_object_model_3d_params
get_object_model_3d_params( : : ObjectModel3D, ParamName : ParamValue)
F1文档查看,有所有想要的信息~
然后选择ParamName是'primitive_parameter',取出法向量
选择ParamName是'primitive_pose',取出位姿
代码如下:
X:=[-0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04]
Y:=[-0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04]
Z:=[-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0]
*生成3D模型
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
dev_open_window(0, 0, 512, 512, 'black', WindowHandle)
*展示一下这个平面
fit_primitives_object_model_3d (ObjectModel3D, ['primitive_type','fitting_algorithm'], ['plane','least_squares_tukey'], ObjectModel3DOut)
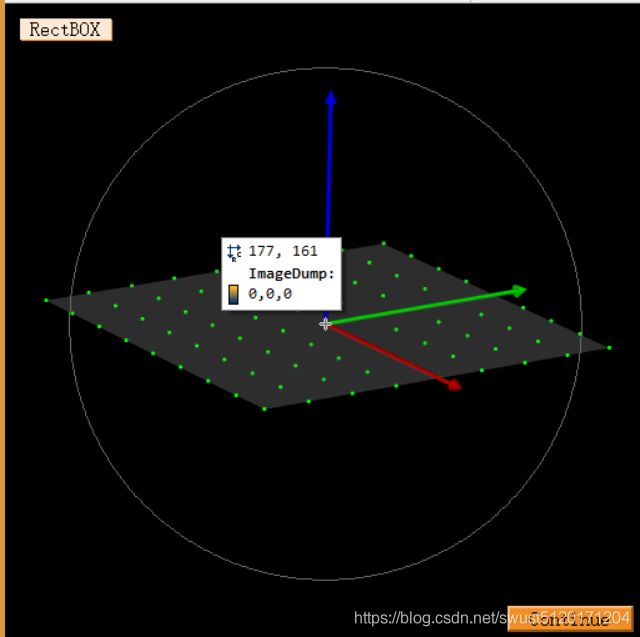
visualize_object_model_3d (WindowHandle,[ObjectModel3D,ObjectModel3DOut], [],[], \
['color_0','color_1','alpha_1','disp_pose'], ['green','gray',0.5,'true'],'RectBOX', [], [], Pose)
*获取法向量,Normal的前三个数值就是单位法向量
get_object_model_3d_params (ObjectModel3DOut, 'primitive_parameter', Normals)平面图如下:
单位法向量:
刚好是Z轴正方向的那个法向量。