2022年全国研究生数学建模竞赛华为杯F题COVID-19疫情期间生活物资的科学管理问题求解全过程文档及程序

2022年全国研究生数学建模竞赛华为杯

F题 COVID-19疫情期间生活物资的科学管理问题

原题再现：

  一、背景介绍
  进入2022年以来全国范围内陆续出现了多次较大规模疫情爆发事件[1-2]。在大规模疫情爆发期间由于我国采用封闭式管理方式来实现疫情的快速清零，从而疫情期间各类人群的科学管理变得尤为重要[3-4]。由于大部分地区管理者尚未遇见如此大规模爆发的疫情及不同地区疫情爆发时长、人口规模与地理位置等的差异性，众多地区仍未形成较为科学的统一管理模式，使得疫情的清零周期普遍较长。在对大规模的人员采用封闭式管理的情况下，关联地区的经济发展持续放缓，再考虑到全球经济形势及疫情等因素所导致的经济下行压力[5]，我们急需形成规范化的疫情快速清零机制。
  在疫情期间由于对确诊病例、无症状感染者及密切接触者采用集中治疗或隔离的手段，因此此类人群的科学管理较易实现。然而，对于大量、分散居家隔离人员实现统一化管理成为新的难点问题，目前我们所搜集到的典型问题包括如下三个方面：
  （1）生活物资的科学发放问题：在疫情期间由于采用封闭式管理方式，居民的生活物资发放成为所有问题中的焦点问题。如果发放不当不仅会影响隔离居民的生活，还很有可能在生活物资发放过程中造成疫情的二次传播。
  （2）特殊群体的管理问题：小区里往往具有一定规模的行动不便或信息化水平较低的特殊群体。对于这些人群的管理会消耗掉大量的人力资源，加剧了疫情期间防疫人员与资源的紧缺。另外，在大规模疫情期间高校学生们的科学管理问题也是需要重点关注的问题。
  （3）为援助与医务人员提供高效服务问题：在疫情期间援助与医务人员的服务对疫情的防控与治疗起到无可替代的作用。只有对这些人群实现高效的服务，才能够更快地控制疫情[6]。然而，援助与医务人员所需的物资与广大居民的需求可能存在显著差异，我们需要付出更多的时间和精力去凑齐相关物资。这项工作也是一项不可忽视的重要任务。

  本赛题聚焦第一个问题，解决疫情期间生活物资的科学管理问题，在全面提高疫情防控效率的同时，努力节约相关部门的人员投入与经费支出，并为今后的应急管理方案打下坚实的理论与实践基础。
  二、问题的描述
  疫情期间生活物资的管理是一项复杂的系统工程。交警、高速公路管理部门、商务局、邮政部门、防疫部门、民委及市场监管局等均参与其中。通常疫情发现的越早越有利于疫情的防控，然而在实际管理过程中仍会出现疫情发现较晚的特殊情况。如果疫情发现较晚，大量的人群间有了错综复杂的交互，全民居家隔离与全民核酸检测成为了较优的选择。由此产生的大规模居家人群的科学管理成为了新的难点。
  在大规模疫情爆发期间可能会涉及到成百上千的小区及几百万规模的居家隔离人员。不同小区人口规模不同且组织化水平参差不齐。在疫情爆发初期，不少居民得到可能封城的消息后都去购买生活物资而导致大规模人员聚集。没有采购到足够物资的人群也通过其它平台订购生活物资，增加了疫情传播的风险。当时网络平台上的讨论也说明在疫情的初期存在一定程度的管理混乱，百姓们唯恐得不到足够数量的生活物资而恐慌[7-8]，疫情期间生活物资的科学管理被推上了风口浪尖。
  相关数据分析表明，在疫情期间政府完全有能力调动足够数量的生活物资。只是生活物资发放给社区居民的渠道不畅[9]。因此我们需要制定科学的管理方案来高效应对疫情。值得庆幸的是在最近几个月在不同城市大规模疫情的控制过程中我们积累下了众多宝贵的经验。其中采用蔬菜包的做法为疫情期间居民生活物资的有效发放起到了一定的作用。
  蔬菜包主要以新鲜蔬菜为主，因其人人每天必须，且保质期相对较短，从而配送频率较高，造成人员间密切接触。米、面、油及肉等虽然也是居民迫切需要的生活物资，但因保质期长且主要由政府储备，因此其配送任务可以穿插到蔬菜包的配送过程。另外，水果也是居民们普遍需要的，如果生产出来却无法销售也对经济发展不利，因此在不增加疫情传播风险的情况下，也要考虑诸如水果等非必须食品的科学供应。由于蔬菜无论在数量、频次、影响等方面都更突出，故本赛题聚焦蔬菜的科学供应。
  三、需要解决的问题
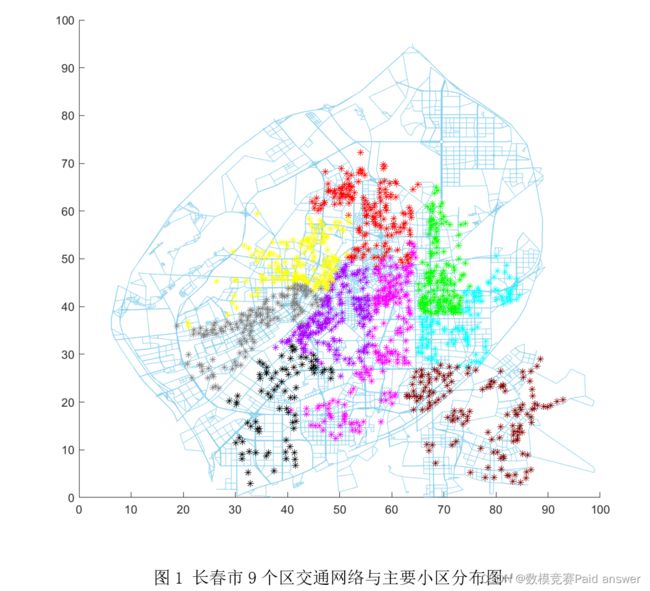
  目前我们搜集到了长春市9个区的各项基础数据，不同区的隔离人口数量与生活物资投放点数量如附件2所示。这9个区的交通网络基础数据和主要小区的相关数据如附件3所示，各区交通网络图及其小区的分布图如图1所示。请你们结合数学建模的方法解决如下几个问题：

  问题一：各种生活物资的大规模流动方式对疫情的影响
  不少城市的疫情在短时间内无法得到快速控制，反思其原因，有一种观点认为疫情的发展或被控制扑灭与生活物资发放方式有关。请结合附件1中所提供的长春市COVID-19疫情期间病毒感染人数数据及其它附件数据或你们能搜集到的数据对长春市实行发放蔬菜包前后效果进行判别与分析，以利今后的防控工作。
  问题二：生活物资投放点数量与位置问题
  在疫情爆发初期长春市的生活物资主要通过若干个投放点进行发放。考虑到在疫情初期既需要大量的人力资源又同时要求尽量减少人员流动、接触，投放点的数量显得尤为重要。在附件2中提供了当时长春市不同区域投放点数量分布结果。请结合附件3中和附件4中有关数据，讨论投放点数量的合理性，并通过数学建模进行适当的优化。另外，请充分考虑未来疫情、自然灾害等特殊事件，对于政府储备物资和大规模物资分拣场所的位置与数量规模进行合理规划，并提出最优的选址数量、规模及其潜在的备用场所位置。
  注：请务必将相关结果以表格的形式放置在正文中,其中主要参数包括选址位置及所属区域、选址半径、管辖范围小区个数及管辖范围内人口数等关键信息应该体现在表格中。
  问题三：生活物资的科学发放问题
  在疫情期间生活物资的发放过程中蔬菜作为一类人们急需且保质期较短的特殊产品，其分配的效果比较重要。长春市经过一段探索发现蔬菜包形式既减轻本市志愿者的数量与工作量又减少人员对蔬菜的接触。请依据附件5分析蔬菜包需求、发放规律，并根据附件3中的各小区位置与人口信息，评价并调整4月10日至4月15日蔬菜包供应方案。
  问题四：为长春市做好大规模封控情况下居民生活物资有序发放预案
  长春市三月的疫情虽然安全扑灭，但未雨绸缪，请你们在第二、三问的基础上，结合附件3给出的长春市街道和小区情况的表格，做出特殊时期保障居民生活物资供应的详细预案（有序网络图）。网络上游是各项物资来源（每个区选一个地点，参赛队可自行根据坐标选择），中游是各项物资的集散地(集散地数量自行选择，可以先按附件2设置，再调整优化)，网络下游是长春市所有小区。物流是一个周期内各天通过网络各条边所运输的各项生活物资的数量（开始可以只考虑蔬菜，不同日期可以发送不同品种蔬菜以增加居民的蔬菜品种）。开始时，网络的各条边可以不使用真实的街道，认为两点之间由最短路连接。后来可以选择少数行政区按真实街道选择路线，直至全市。由于是特殊时期，所以节省人力（工作量按运输里程与小区居民人数乘积计算）是最重要的指标，同时希望减少人员的直接、间接接触。在完成有序网络图后请进一步考虑用卡车运送物资，大卡车每辆可装10吨，小卡车每辆可装4吨,观察预案有无显著不同。
  注：请以图形或表格的方式精简地将相关结果在正文中表述出来，并请对照指标分析与评价你们给出的发放预案的优势。
  四、数据说明
  （1）附件1：长春市COVID-19疫情期间病毒感染人数数据（数据来自长春市卫生健康委员会网站http://wjw.changchun.gov.cn）
  （2）附件2：长春市9个区隔离人口数量与生活物资投放点数量（数据为某天的截面数据，不同天的人口数可能存在误差）
  （3）附件3：长春市9个区交通网络数据和主要小区相关数据（数据为网络抓取的近似数据）
  （4）附件4：长春市疫情期间每日生活物资相关数据（数据由长春市商务局提供）
  （5）附件5：长春市疫情期间每日各区蔬菜包相关数据（数据由长春市商务局提供）

整体求解过程概述(摘要)

  2022 年以来全国范围内陆续出现了多次较大规模疫情爆发事件，在严峻的疫情期间，生活物资的科学发放问题亟待解决。本文利用文本挖掘、多元因子分析、聚类分析、Dijkstra最短路径等算法，结合题目所提供的长春市的数据，为长春市各区物资投放点的数量及位置、物资发放方案、运送物资的路线规划做出了合理分析及优化。
  针对问题一，本文采用基于文本挖掘的多元因子分析方法，使用 Python 软件，对蔬菜包、自采、对接等关键词进行检索，确定了 3 月 26 日为蔬菜包发放的起始时间。考虑当地政府防疫政策、蔬菜价格、企业是否营运等多个因素，建立数学模型，结合长春市疫情期间病毒感染人数数据进行多元因子分析，最后得到长春市实行发放蔬菜包前后效果的对比分析结果。
  针对问题二，本文采用基于欧氏距离的聚类分析方法，首先判别主要小区物资投放点是否合理，甄别出不合理区域，将附件所提供的交通路口节点与交通路口路线终点进行表关联，按区域划分确定物资投放点数量及备用物资投放点数量，将所得到的物资投放点横纵坐标与附件 3 中各主要小区数据的横纵坐标作欧氏距离计算，得出物资投放点所属区域，进而计算出选址半径，并利用 K-means 聚类明确物资投放点辐射范围。最后依托题中所给数据，给出政府储备物资和大规模物资分拣场所的位置与最优选址数量、规模。
  针对问题三，本文基于人口信息、蔬菜包发放信息及小区位置制定最优供应方案。首先为了方便读取数据，对题中所给信息进行规整化处理，绘制不同区域接收与自采蔬菜包随日期变化曲线图、堆叠柱状图等，深度分析得出长春市蔬菜包发放规律：蔬菜包采购与发放数量与感染人数呈正相关。联系问题一结果与附件所给信息，判断出现有蔬菜包供应方案不合理，构建多元非线性回归模型，使用 SPSS 软件，经过影响因素间相关性分析和模型显著检验，最后得出预测值，将其作为优化后蔬菜包供应方案。
  针对问题四，在第二、三问的基础之上，结合附件 3 给出的长春市街道和小区情况的表格，做出特殊时期保障居民生活物资供应的详细预案。本文根据附件 2 及搜集到的路网信息和小区数据，采用 Dijkstra 算法确定中游物资集散地和上游物资来源地的选址，并为运送物资规划了最佳路径，绘制出有序网络图。运用遗传算法为各路线分配不同运量的卡车，从而节省人力并减少人员间的直接或间接接触，进而控制疫情的发展。

模型假设：

  根据影响疫情蔓延的因素与题中所给的条件及要求，本文做出以下假设：
  （1） 假设本题附件所提供的数据均真实有效；
  （2） 假设物资投放点运送物资的速度均相同；
  （3） 假设不考虑卡车加速和制动导致的速度变化；
  （4） 假设每个小区的需求量不超过大卡车的运量；
  （5） 卡车不能出现超载情况。

问题分析：

  针对问题一，本文采用基于文本挖掘的多元因子分析方法，使用 Python 软件，对蔬菜包、自采、对接等关键词进行检索，确定了 3 月 26 日为蔬菜包发放的起始时间。考虑当地政府防疫政策、蔬菜价格、企业是否营运等多个因素，建立数学模型，结合长春市疫情期间病毒感染人数数据进行多元因子分析，最后得到长春市实行发放蔬菜包前后效果的对比分析结果。
  针对问题二，本文采用基于欧氏距离的聚类分析方法，首先判别主要小区物资投放点
是否合理，甄别出不合理区域，将附件所提供的交通路口节点与交通路口路线终点进行表
关联，按区域划分确定物资投放点数量及备用物资投放点数量，将所得到的物资投放点横
纵坐标与附件 3 中各主要小区数据的横纵坐标作欧氏距离计算，得出物资投放点所属区域，
进而计算出选址半径，并利用 K-means 聚类明确物资投放点辐射范围。最后依托题中所给
数据，给出政府储备物资和大规模物资分拣场所的位置与最优选址数量、规模。
  针对问题三，本文基于人口信息、蔬菜包发放信息及小区位置制定最优供应方案。首先为了方便读取数据，对题中所给信息进行规整化处理，绘制不同区域接收与自采蔬菜包随日期变化曲线图、堆叠柱状图等，深度分析得出长春市蔬菜包发放规律：蔬菜包采购与发放数量与感染人数呈正相关。联系问题一结果与附件所给信息，判断出现有蔬菜包供应方案不合理，构建多元非线性回归模型，使用 SPSS 软件，经过影响因素间相关性分析和模型显著检验，最后得出预测值，将其作为优化后蔬菜包供应方案。

  虽然长春此次疫情被扑灭，但是疫情形势依然不容乐观，我们需要未雨绸缪、做好疫情反扑的应对准备。针对问题四，在第二、三问的基础之上，结合附件 3 给出的长春市街道和小区情况的表格，做出特殊时期保障居民生活物资供应的详细预案。本文根据附件 2及搜集到的路网信息和小区数据，采用 Dijkstra 算法确定中游物资集散地和上游物资来源地的选址，并为运送物资规划了最佳路径，绘制出有序网络图。运用遗传算法为各路线分配不同运量的卡车，从而节省人力并减少人员间的直接或间接接触，进而控制疫情的发展。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分Python程序如下:

def getNameData(min_row, max_row, min_col, max_col, workbook):
 data = []
 for row in workbook.iter_rows(min_row=min_row, max_row=max_row, min_col=min_col, 
max_col=max_col):
 line = []
 for cell in row:
 line.append(cell.value)
 data.append(line)
 return data
def getNameData0(min_row, max_row, min_col, max_col, workbook):
 data = []
 for row in workbook.iter_rows(min_row=min_row, max_row=max_row, min_col=min_col, 
max_col=max_col):
 line = []
 for cell in row:
 line.append(cell.value)
 data.append(line[0])
 return data
import openpyxl
def saveData(data, name):
 wb_write1 = openpyxl.Workbook()
 ws_write1 = wb_write1['Sheet']
 ws_write1.append(
 ['日期', '变化率'])
 for i in range(len(data)):
 d = tuple(data[i])
 ws_write1.append(d)
 wb_write1.save(name)
def removeNone(who):
 return [item if item != None else 0 for item in who]

import openpyxl
from read import getNameData, getNameData0, saveData, removeNone
import numpy as np
workbook = openpyxl.load_workbook('附件 1：长春市 COVID-19 疫情期间病毒感染人数数
据.xlsx').worksheets[0]
workbook1 = openpyxl.load_workbook('附件 1：长春市 COVID-19 疫情期间病毒感染人数数
据.xlsx').worksheets[1]
label_to_name = {}
date_save, sheet1_save, sheet2_save = [], [], []
dh, dh_data = getNameData(1, 1, 2, 10, workbook)[0], getNameData(12, 12, 2, 10, workbook)[0]
h11 = getNameData0(27, 59, 11, 11, workbook)
real, real_data = getNameData(1, 1, 12, 28, workbook)[0], [item if item != None else 0 for 
item in getNameData(12, 12, 12, 28, workbook)[0]]
q1 = getNameData0(2, 26, 11, 11, workbook)
h1 = getNameData0(27, 82, 11, 11, workbook)
print(np.mean(q1)>np.mean(h11))
#print(np.mean(q1)>np.mean(h1))
date1 = getNameData0(2, 26, 1, 1, workbook)
date2 = getNameData0(27, 82, 1, 1, workbook)
date = date1 + date2
date = [item+'日' for item in date]
q2 = getNameData0(2, 26, 2, 2, workbook1)
q2 = [item if item != None else 0 for item in q2]
h2 = getNameData0(27, 82, 2, 2, workbook1)
print(np.sum([(item-np.mean(q1))**2 for item in q1])/len(q1))
#print(np.sum([(item-np.mean(h11))**2 for item in h11])/len(h11))
print(np.sum([(item-np.mean(h1))**2 for item in h11])/len(h1))
#####
print(np.sum([(item-np.mean(q2))**2 for item in q2])/len(q2))
print(np.sum([(item-np.mean(h2))**2 for item in h2])/len(h2))
#####
total1, total2 = q1 + h1, q2 + h2
for i in range(len(total1)):
 if i < len(total1)-1:
 try:
 p = (total1[i+1] - total1[i])/total1[i]
 except:
 p = 0.0
 t = date[i]+'-'+date[i+1]
 date_save.append(t)
 sheet1_save.append([t, round(p, 4)])
for j in range(len(dh_data)):
for i in range(len(real_data)):
 if dh_data[j] == real_data[i]:
 label_to_name[real[i]] = dh[j]
print(label_to_name)
for i in range(0, len(total2)):
 if i < len(total2)-1:
 try:
 p = (total2[i+1] - total2[i])/total2[i]
 except:
 p = 0.0
 sheet2_save.append(round(p, 4))
sheet2_save = [[date_save[i], sheet2_save[i]]for i in range(len(sheet2_save))]
saveData(sheet1_save, '新增本土感染者变化率.xlsx')
saveData(sheet2_save, '新增无症状感染者变化率.xlsx')
print(np.mean(removeNone(getNameData0(2,26,2,2,workbook))))
print(np.mean(removeNone(getNameData0(27,59,2,2,workbook))))
print(np.mean(removeNone(getNameData0(2,26,3,3,workbook))))
print(np.mean(removeNone(getNameData0(27,59,3,3,workbook))))
print(np.mean(removeNone(getNameData0(2,26,4,4,workbook))))
print(np.mean(removeNone(getNameData0(27,59,4,4,workbook))))
print(np.mean(removeNone(getNameData0(2,26,5,5,workbook))))
print(np.mean(removeNone(getNameData0(27,59,5,5,workbook))))
print(np.mean(removeNone(getNameData0(2,26,6,6,workbook))))
print(np.mean(removeNone(getNameData0(27,59,6,6,workbook))))
print(np.mean(removeNone(getNameData0(2,26,7,7,workbook))))
print(np.mean(removeNone(getNameData0(27,59,7,7,workbook))))
print(np.mean(removeNone(getNameData0(2,26,8,8,workbook))))
print(np.mean(removeNone(getNameData0(27,59,8,8,workbook))))
print(np.mean(removeNone(getNameData0(2,26,9,9,workbook))))
print(np.mean(removeNone(getNameData0(27,59,9,9,workbook))))
print(np.mean(removeNone(getNameData0(2,26,10,10,workbook))))
print(np.mean(removeNone(getNameData0(27,59,10,10,workbook))))

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可