强化学习笔记_8_连续控制
1. 离散控制与连续控制 Discrete VS Continuous Control
-
Discrete Action Space
-
Continuous Action Space
-
DQN算法、Policy Network等可以解决离散控制问题,输出为一个确定维度的向量
-
Discretization,离散化,将动作空间变为有限的离散空间;适用于维度比较小的问题。
设控制问题的自由度为 d d d,则动作空间为 d d d维的,离散化时,离散空间内点的数量随着 d d d指数增加,导致维数灾难、训练困难。
-
其他方法:Deterministic policy network; Stochastic policy network.
2. Deterministic Policy Gradient (DPG, 确定策略梯度)
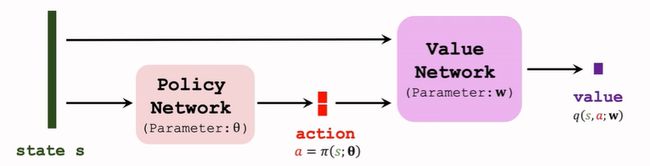
2.1. Deterministic Actor-Critic
- deterministic policy network (actor): a = π ( s ; θ ) a=\pi(s;\theta) a=π(s;θ),输出不是一个概率,而是一个具体的动作 a a a,输出维度为动作空间的维数;
- value network (critic): q ( s , a ; w ) q(s,a;w) q(s,a;w);
2.2. Updating Value Network by TD
-
Transition: ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1)
-
Value network:
q t = q ( s , a ; w ) q t + 1 = q ( s t + 1 , a t + 1 ; w ) , w h e r e a t + 1 ′ = π ( s t + 1 ; θ ) \begin{aligned} q_t&=q(s,a;w) \\q_{t+1}&=q(s_{t+1},a_{t+1};w),where\quad a_{t+1}'=\pi(s_{t+1};\theta) \end{aligned} qtqt+1=q(s,a;w)=q(st+1,at+1;w),whereat+1′=π(st+1;θ) -
TD error: δ t = q t − ( r t + γ ⋅ q t + 1 ) \delta_t=q_t-(r_t+\gamma\cdot q_{t+1}) δt=qt−(rt+γ⋅qt+1)
TD target: y t = r t + γ ⋅ q t + 1 y_t=r_t+\gamma\cdot q_{t+1} yt=rt+γ⋅qt+1
-
Update: w ← w − α ⋅ δ t ⋅ ∂ q ( s t , a t ; w ) ∂ w w\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial q(s_t,a_t;w)}{\partial w} w←w−α⋅δt⋅∂w∂q(st,at;w)
2.3. Updating Policy Network by DPG
Goal: Increasing q ( s , a ; w ) q(s,a;w) q(s,a;w), where a = π ( s ; θ ) a=\pi(s;\theta) a=π(s;θ)
DPG:
g = ∂ q ( s , π ( s ; θ ) ; w ) ∂ θ = ∂ a ∂ θ ⋅ ∂ q ( s , a ; w ) ∂ a g = ∂ q ( s , π ( s ; θ ) ; w ) ∂ θ = ∂ a ∂ θ ⋅ ∂ q ( s , a ; w ) ∂ a g=\frac{\partial q(s,\pi(s;\theta);w)}{\partial \theta}=\frac{\partial a}{\partial \theta}\cdot\frac{\partial q(s,a;w)}{\partial a}g=\frac{\partial q(s,\pi(s;\theta);w)}{\partial \theta}=\frac{\partial a}{\partial \theta}\cdot\frac{\partial q(s,a;w)}{\partial a} g=∂θ∂q(s,π(s;θ);w)=∂θ∂a⋅∂a∂q(s,a;w)g=∂θ∂q(s,π(s;θ);w)=∂θ∂a⋅∂a∂q(s,a;w)
Gradient ascent: θ ← θ + β ⋅ g \theta\leftarrow \theta+\beta\cdot g θ←θ+β⋅g
2.4. Improvement: Using Target Network
-
Bootstrapping
TD error δ t = q t − ( r t + γ ⋅ q t + 1 ) \delta_t=q_t-(r_t+\gamma\cdot q_{t+1}) δt=qt−(rt+γ⋅qt+1)导致Bootstrapping,如果初始产生了高估(低估),则会导致后续的高估(低谷)。
解决方案:使用不同的网络计算TD target——target networks
-
target networks
-
Value network: q t = q ( s t , a t ; w ) q_t=q(s_t,a_t;w) qt=q(st,at;w)
-
Value network: q t + 1 = q ( s t + 1 , a t + 1 ′ ; w − ) , w h e r e a t + 1 ′ = π ( s t + 1 ; θ − ) q_{t+1}=q(s_{t+1},a'_{t+1};w^-),where\quad a_{t+1}'=\pi(s_{t+1};\theta^-) qt+1=q(st+1,at+1′;w−),whereat+1′=π(st+1;θ−)
Target value network: q ( s t , a t ′ ; w − ) q(s_{t},a'_{t};w^-) q(st,at′;w−)
Target policy network: π ( s t ; θ − ) \pi(s_{t};\theta^-) π(st;θ−)
-
-
用到的算法概括如下:
-
Updating target network
hyper-parameter τ ∈ ( 0 , 1 ) \tau\in(0,1) τ∈(0,1),使用加权平均 (weighted averaging) 更新参数:
w − ← τ ⋅ w + ( 1 − τ ) ⋅ w − θ − ← τ ⋅ θ + ( 1 − τ ) ⋅ θ − \begin{aligned} w^-&\leftarrow\tau\cdot w+(1-\tau)\cdot w^- \\\theta^-&\leftarrow\tau\cdot \theta+(1-\tau)\cdot \theta^- \end{aligned} w−θ−←τ⋅w+(1−τ)⋅w−←τ⋅θ+(1−τ)⋅θ−
target network中的参数依然与原网络相关,故无法完全解决bootstrapping
2.5. Improvements
- Target network
- Experience relay
- Multi-step TD target
2.6. Stochastic Policy VS Deterministic Policy
3. Stochastic Policy for Continuous Control (离散策略)
3.1. Policy Network
-
Univariate Normal Distribution (单变量正态分布)
考虑单自由度情况,自由度 d = 1 d=1 d=1,均值(mean) μ \mu μ和标准差(std) σ \sigma σ是状态 s s s的函数;
使用正态分布的概率密度函数作为策略函数:
π ( a ∣ s ) = 1 2 π σ ⋅ exp ( − ( a − μ ) 2 2 σ 2 ) \pi(a|s)=\frac{1}{\sqrt{2\pi}\sigma}\cdot\exp(-\frac{({a-\mu})^2}{2\sigma^2}) π(a∣s)=2πσ1⋅exp(−2σ2(a−μ)2) -
Multivariate Normal Distribution (多变量正态分布)
自由度为 d d d,动作空间action a a a为 d d d维,均值和标准差分别为 μ , σ : S → R d \pmb{\mu},\pmb{\sigma}:\mathcal{S}\rightarrow\R^d μ,σ:S→Rd,输入为状态 s s s,输出为 d d d维向量。
使用 μ i , σ i \mu_i,\sigma_i μi,σi表示 μ ( s ) , σ ( s ) \pmb{\mu}(s),\pmb\sigma(s) μ(s),σ(s)的第 i i i个分量。假设动作空间内各个维度都是独立的,则PDF:
π ( a ∣ s ) = Π i = 1 d 1 2 π σ i ⋅ exp ( − ( a i − μ i ) 2 2 σ i 2 ) \pi(a|s)=\Pi_{i=1}^d \frac{1}{\sqrt{2\pi}\sigma_i}\cdot\exp(-\frac{(a_i-\mu_i)^2}{2\sigma_i^2}) π(a∣s)=Πi=1d2πσi1⋅exp(−2σi2(ai−μi)2) -
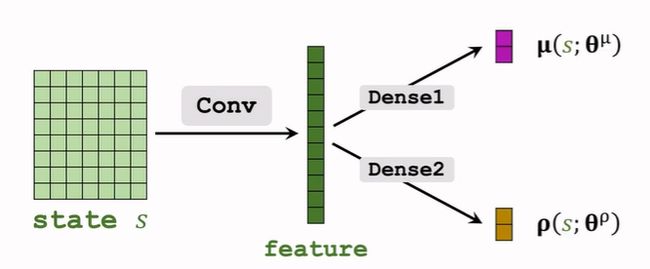
Function Approximation
-
使用神经网络 μ ( s ; θ μ ) \pmb\mu(s;\pmb\theta^\mu) μ(s;θμ)对均值 μ ( s ) \pmb\mu(s) μ(s)进行近似;
-
使用神经网络 σ ( s ; θ σ ) \pmb\sigma(s;\pmb\theta^\sigma) σ(s;θσ)对均值 σ ( s ) \pmb\sigma(s) σ(s)进行近似(效果不好); -
对方差的对数进行近似,使用神经网络 ρ ( s ; θ ρ ) \pmb\rho(s;\theta^\rho) ρ(s;θρ)对 ρ \rho ρ近似
ρ i = ln σ i 2 , i = 1 , ⋅ ⋅ ⋅ , d \rho_i=\ln\sigma_i^2,i=1,···,d ρi=lnσi2,i=1,⋅⋅⋅,d
-
-
Continuous Control
-
观测得到当前状态 s t s_t st;
-
计算均值和方差 μ ^ = μ ( s ; θ μ ) \pmb{\hat{\mu}}=\pmb\mu(s;\theta^\mu) μ^=μ(s;θμ),方差 ρ ^ = μ ( s ; θ ρ ) , σ ^ i 2 = exp ( ρ ^ i ) \pmb{\hat{\rho}}=\pmb\mu(s;\theta^\rho),\hat{\sigma}_i^2=\exp(\hat{\rho}_i) ρ^=μ(s;θρ),σ^i2=exp(ρ^i);
-
随机采样得到动作
a ∼ N ( μ ^ , σ ^ i ) , i = 1 , ⋅ ⋅ ⋅ , d a\sim\mathcal{N}(\hat{\mu},\hat{\sigma}_i),i=1,···,d a∼N(μ^,σ^i),i=1,⋅⋅⋅,d
-
-
Training Policy Network
-
Auxiliary network,辅助神经网络
-
Policy gradient methods
- option 1: REINFORCE
- option 2: Actor-Critic
-
3.2. Training (1/2): Auxiliary Network
-
Stochastic policy gradient:
g ( a ) = ∂ ln π ( a ∣ s ; θ ) ∂ θ ⋅ Q π ( s , a ) g(a)=\frac{\partial \ln\pi(a|s;\theta)}{\partial\theta}\cdot Q_\pi(s,a) g(a)=∂θ∂lnπ(a∣s;θ)⋅Qπ(s,a) -
Policy network:
π ( a ∣ s ; θ μ , θ ρ ) = Π i = 1 d 1 2 π σ i ⋅ exp ( − ( a i − μ i ) 2 2 σ i 2 ) \pi(a|s;\pmb\theta^\mu,\pmb\theta^\rho)=\Pi_{i=1}^d \frac{1}{\sqrt{2\pi}\sigma_i}\cdot\exp(-\frac{(a_i-\mu_i)^2}{2\sigma_i^2}) π(a∣s;θμ,θρ)=Πi=1d2πσi1⋅exp(−2σi2(ai−μi)2)
Log of policy network:
ln π ( a ∣ s ; θ μ , θ ρ ) = ∑ i = 1 d [ − ln σ i − ( a i − μ i ) 2 2 σ i 2 ] + c o n s t = ∑ i = 1 d [ − ρ i 2 − ( a i − μ i ) 2 2 ⋅ exp ( ρ i ) ] + c o n s t \begin{aligned} \ln\pi(a|s;\pmb\theta^\mu,\pmb\theta^\rho) &=\sum_{i=1}^d [-\ln\sigma_i-\frac{(a_i-\mu_i)^2}{2\sigma_i^2}]+const \\&=\sum_{i=1}^d [-\frac{\rho_i}{2}-\frac{(a_i-\mu_i)^2}{2\cdot\exp(\rho_i)}]+const \end{aligned} lnπ(a∣s;θμ,θρ)=i=1∑d[−lnσi−2σi2(ai−μi)2]+const=i=1∑d[−2ρi−2⋅exp(ρi)(ai−μi)2]+const -
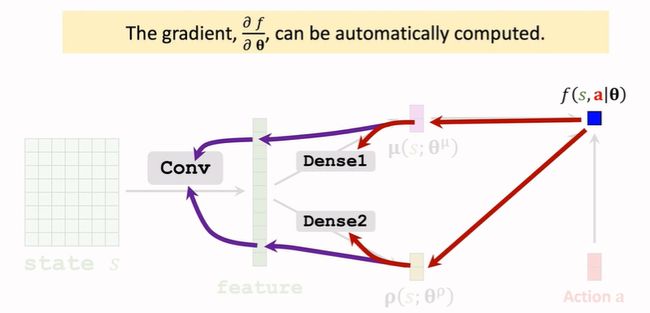
Auxiliary Network:
f ( s , a ; θ ) = ∑ i = 1 d [ − ρ i 2 − ( a i − μ i ) 2 2 ⋅ exp ( ρ i ) ] , θ = ( θ μ , θ ρ ) f(s,a;\pmb\theta)=\sum_{i=1}^d [-\frac{\rho_i}{2}-\frac{(a_i-\mu_i)^2}{2\cdot\exp(\rho_i)}],\pmb\theta=(\pmb\theta^\mu,\pmb\theta^\rho) f(s,a;θ)=i=1∑d[−2ρi−2⋅exp(ρi)(ai−μi)2],θ=(θμ,θρ)

3.2. Training (2/2): Policy gradient methods
-
Stochastic policy gradient:
f ( s , a ; θ ) = ln π ( a ∣ s ; θ ) + c o n s t g ( a ) = ∂ ln π ( a ∣ s ; θ ) ∂ θ ⋅ Q π ( s , a ) \begin{aligned} f(s,a;\pmb\theta)&=\ln\pi(a|s;\pmb\theta)+const \\g(a)&=\frac{\partial \ln\pi(a|s;\pmb\theta)}{\partial\theta}\cdot Q_\pi(s,a) \end{aligned} f(s,a;θ)g(a)=lnπ(a∣s;θ)+const=∂θ∂lnπ(a∣s;θ)⋅Qπ(s,a)
得到:
g ( a ) = ∂ f ( s , a ; θ ) ∂ θ ⋅ Q π ( s , a ) g(a)=\frac{\partial f(s,a;\pmb\theta)}{\partial\theta}\cdot Q_\pi(s,a) g(a)=∂θ∂f(s,a;θ)⋅Qπ(s,a)
接下来对 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)进行近似。 -
option 1: REINFORCE
蒙特卡洛近似,使用观测值 u t u_t ut进行近似 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a),参数更新:
θ ← θ + β ⋅ ∂ f ( s , a ; θ ) ∂ θ ⋅ u t \pmb\theta\leftarrow\pmb\theta+\beta\cdot\frac{\partial f(s,a;\pmb\theta)}{\partial\pmb\theta}\cdot u_t θ←θ+β⋅∂θ∂f(s,a;θ)⋅ut -
option 2: Actor-Critic
使用价值网络 q ( s , a ; w ) q(s,a;\pmb w) q(s,a;w)进行近似 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a),参数更新:
θ ← θ + β ⋅ ∂ f ( s , a ; θ ) ∂ θ ⋅ q ( s , a ; w ) \pmb\theta\leftarrow\pmb\theta+\beta\cdot\frac{\partial f(s,a;\pmb\theta)}{\partial\pmb\theta}\cdot q(s,a;\pmb w) θ←θ+β⋅∂θ∂f(s,a;θ)⋅q(s,a;w)
使用TD learning训练价值网络 q ( s , a ; w ) q(s,a;\pmb w) q(s,a;w)
3.3. Improvement: Policy gradient with baseline
- Reinforce: Reinforce with baseline.
- Actor-Critic: Advantage Actor-Critic (A2C).