PID智能小车快速入门(一)
一、基本PID原理
1、什么是PID?
PID控制器是一种线性控制器,通俗的来讲如人走直线一样,眼睛是观测器,下肢为执行器,当走偏了由眼睛观测得出当前位置和直线的偏差,由人脑根据偏差调整脚步回归直线的过程就是一个负反馈调节的过程,而PID控制器就是得到偏差,然后通过PID算法,将输出作用于被控对象上,使其达到并在给定值附近稳定,如水温的恒温控制,电机转速控制,舵机打角控制。PID作为一种简单的控制算法广为应用。
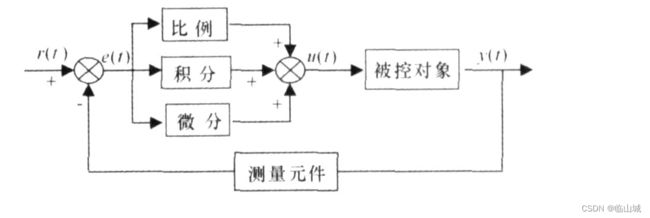
以下是典型PID的控制结构图
偏差err=给定值-测量值。
以小车编码电机为例 偏差=目标值转速(编码器值)-编码器采集值。
2、PID算法的构成
网上关于PID的教程以及算法的推导内容丰富,本文章旨在快速部署PID算法于控制器上,所以算法推导不过多讲解。
以下列出基本公式:
可以很明显看出基本PID整体算法由 比例环节(P) : Kp*err(t),积分环节(I) : Ki*每次偏差的累积, 微分环节(D) : Kd*偏差的变化率(当前的偏差-上一次的偏差)。
由公式看出式子中含有积分时间常Ti,微分时间常数Td所以通常PID算法应部署在有固定时间周期运行的部分,如有固定周期的中断内。
比例环节:比例环节没有时间常数,所以它成比例的反应偏差信号,偏差一旦产生,控制器立即执行,以减少偏差。体现出当前控制。
积分环节:积分环节主要作用是消除稳态误差,使得输出更逼近目标值,积分强弱取决于时间常数的大小,由Ki决定,预防偏差累积过大一般需要对积分值做限值处理。体现出历史控制。
微分环节:微分环节反应偏差值的变化率,能够估计偏差变化趋势,当过大偏差到来时提前引入一个有效的修正信号,提高系统速度,减少调节时间。体现出将来控制。
总结:PID控制过程=给定目标值----->观察实际值----->得出偏差----->当前+历史+预判=下一个时刻应该输出值。
二、算法转换
1、位置式PID
公式:输出值=比例常数(Kp)* 偏差值 + 积分常数(Ki)* 累积偏差值 + 微分常数(Kd)* (当前偏差 - 上一次偏差)
累积偏差值 + = 当前偏差
最小累积偏差<=累积偏差值<=最大累积偏值
2、增量式PID
增量式PID实际上表示的是位置PID的变化量化简后得出。
公式:输出值 + = Kp * ( 当前偏差 - 上一次偏差 ) + Ki * 当前偏差 + Kd * [当前偏差 - 2*上一次偏差 + 上上次偏差(err(k-2))]
3、总结对比
输出不同:位置式pid输出为控制值,而增量式pid输出为控制值的变化量。
积分环节:位置式pid带有积分环节,而增量式只是对前两次偏差进行运算无积分环节。
应用场合:位置式pid常用于无积分环节执行机构如舵机,电磁阀等。增量式pid常用于有积分环节执行机构如步进电机,直流电机。
注:还常采用PD、PI控制等可以自己尝试使用。PID控制算法是一种比较常见的控制算法,还有经典的LQR,大林算法等等读者可以自行学习比较优缺点应用场合。下一章会讲解进一步根据控制需要对应变化改进的PID算法。
三、python代码仿真
text.py
#text.py
import PID #导入上面的PID算法
from time import sleep
#导入绘图
import matplotlib.pyplot as plt
import numpy as np
def test_pid(Kp, Ki , Kd, target, time):
#位置式PID
pid = PID.Positional_PID(Kp, Ki, Kd, target)
#增量式PID
#pid = PID.Incremental_PID(Kp, Ki, Kd, target)
feedback = 0
feedback_list = []
time_list = []
target_list = []
for i in range(1, 50):
output = pid.PID_OUT(feedback)
feedback +=output #PID控制系统的函数
feedback_list.append(feedback)
target_list.append(target)
time_list.append(i)
#时间间隔实际没有作用,有时间再加上哈哈
sleep(time)
feedback_list[0]=0
target_list[0]=1.1
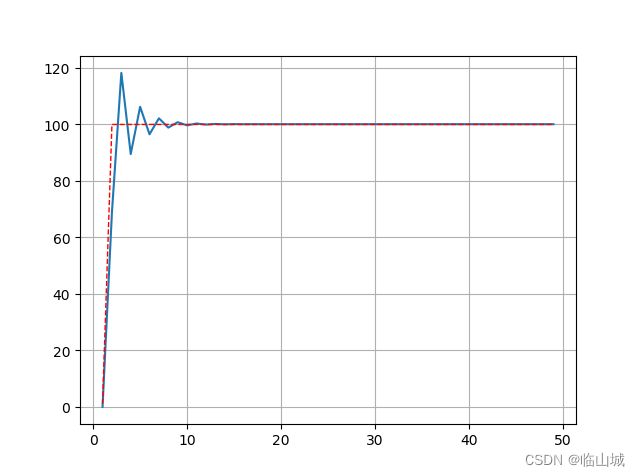
#显示输出曲线
plt.plot(time_list,feedback_list)
#显示目标对比折线
plt.plot(time_list,target_list,color='red',linewidth=1,linestyle='--')
plt.grid(True)
plt.show()
if __name__ == "__main__":
Kp = 1.5
Ki = 0.002
Kd = 0.03
target_value = 100
time = 0.01
test_pid(Kp, Ki, Kd, target_value, time)PID.py
import time
#位置式PID
class Positional_PID(object):
def __init__(self, P, I, D, Target):
#对参数值初始化
self.Target_value = Target #目标值
self.last_error = 0.0 #上一次误差
self.Integral_value_min = -4000 #累积误差的最小限幅
self.Integral_value_max = 4000 #累积误差的最大限幅
self.Output_value = 0.0 #输出值
self.Integral_value = 0.0 #累计值
self.Kp = P #比例常数
self.Ki = I #积分常数
self.Kd = D #微分常数
def PID_OUT(self, Feedback_value):
#根据给定值和返回值求出偏差
error = self.Target_value - Feedback_value
#求偏差累积值
self.Integral_value += error
#对累积值进行限幅
if (self.Integral_value <= self.Integral_value_min):
self.Integral_value = self.Integral_value_min
if (self.Integral_value >= self.Integral_value_max):
self.Integral_value = self.Integral_value_max
#输出值等于比例部分 + 积分部分 + 微分部分
self.Output_value=self.Kp * error + self.Ki * self.Integral_value +self.Kd * (error - self.last_error)
#传递上一次误差
self.last_error = error
return self.Output_value
#增量式PID
class Incremental_PID(object):
def __init__(self, P, I, D, Target):
self.Target_value = Target
self.last_error = 0.0
self.last_last_error = 0.0 #上上次误差
self.Output_value = 0.0
self.Kp = P
self.Ki = I
self.Kd = D
def PID_OUT(self, Feedback_value):
#根据给定值和返回值求出偏差
error = self.Target_value - Feedback_value
#输出值等于比例部分 + 积分部分 + 微分部分
self.Output_value +=self.Kp * (error - self.last_error) + self.Ki * error +self.Kd * (error - 2 * self.last_error + self.last_last_error)
self.last_last_error = self.last_error
self.last_error = error
#print(self.Kp * error)
return self.Output_value
总结:PID算法的构造原理并不难理解,难在调参,调参有经验调参,公式化简的归一化调参,还可以利用Simulink参数自整定等等需要读者自行摸索,由于时间有限程序并未进行图形插值化显示,以及没有体现时间周期对于参数调整的影响,读者自行部署执行机构后尝试后应该可以明白时间常数的影响。由于自身水平有限,第一次编写博客,随时欢迎提出修改意见。