孤立森林（隔离树）译文

摘要

大多数现有的基于模型的异常检测方法都是构造一个正常实例的配置文件，然后将不符合正常配置文件的实例识别为异常。本文提出了一种完全不同的基于模型的方法，它明确地隔离异常，而不是轮廓正常点。据我们所知，孤立的概念在目前的文献中尚未被探索过。隔离的使用使所提出的方法iForest能够在现有方法中不可行的程度上利用子采样，创建了一个具有线性时间复杂度、低常数和低内存要求的算法。我们的经验评估表明，iForest在AUC和处理时间方面优于ORCA，这是一种基于近线性时间复杂度距离的方法，LOF和随机森林，特别是在大数据集中。iForest在具有大量无关属性的高维问题以及训练集不包含任何异常的情况下也很有效。

1、介绍

异常是指与正常实例具有不同的数据特征的数据模式。异常的检测具有重要的相关性，并且通常在各种应用领域提供关键的可操作信息。例如，信用卡交易中的异常情况可能意味着欺诈性地使用信用卡。天文学图像中的一个异常点可能表明发现了一颗新恒星。一种不寻常的计算机网络流量模式可能代表了一种未经授权的访问。这些应用程序要求具有高检测性能和快速执行的异常检测算法。
大多数现有的基于模型的异常检测方法都是构造一个正常实例的配置文件，然后将不符合正常配置文件的实例识别为异常。值得注意的例子，如统计方法[11]、基于分类的方法[1]和基于聚类的方法[5]都使用这种通用方法。这种方法的两个主要缺点是： (i)异常检测器被优化为配置正常实例，但没有优化以检测异常——结果，异常检测的结果可能没有预期的那么好，导致太多的假警报（正常实例被识别为异常）或异常检测到太少；（ii）许多现有方法由于计算复杂度高而被限制在低维数据和数据量小。
本文提出了一种不同类型的基于模型的方法，它明确地隔离异常，而不是分析正常实例。为了实现这一点，我们提出的方法利用了两个异常的定量特性： i)它们是由较少的实例组成的少数值，以及ii)它们具有与正常实例非常不同的属性值。换句话说，异常现象是“少而不同的”，这使得它们比正常的点更容易被孤立。本文证明了可以有效地构造一个树状结构来隔离每个实例。由于它们容易被隔离，异常现象在靠近树根的地方被隔离；而正常的点则被隔离在树的更深处。树的这种隔离特性构成了我们检测异常的方法的基础，我们称这种树为隔离树或iTree。
提出的方法称为隔离森林或iForest，为给定的数据集构建一个iTrees集合，那么异常是那些在iTrees上平均路径长度较短的实例。在这种方法中只有两个变量：要构建的树的数量和子采样的大小。结果表明，iForest的检测性能在非常少的情况下收敛迅速，并且只需要较小的子采样规模就可以实现高效的检测性能。
除了隔离与归档的关键区别外，iForest与现有的基于模型的[11,1,5]、基于距离的[6]和基于密度的方法[4]有以下区别：

1. iTrees的隔离特性使他们能够建立部分模型，并利用在现有方法中不可行的子采样。因为隔离正常点的iTree的大部分不需要进行异常检测；它不需要被构造。小样本量会产生更好的iTrees，因为沼泽和掩蔽效应减少了。
2. iForest不利用距离或密度测量来检测异常。这消除了所有基于距离的方法和基于密度的方法中距离计算的主要计算成本。
3. iForest具有线性时间复杂度，常数低，内存需求低。据我们所知，现有的性能最好的方法在高内存使用[13]下只能实现近似的线性时间复杂度。
4. iForest有能力进行扩展，以处理超大的数据大小和具有大量无关属性的高维问题。

本文的组织结构如下：在第2节中，我们演示了使用一个递归划分数据的iTree在工作中进行的隔离。并提出了一种新的基于iTrees的异常评分方法。在第3节中，我们描述了这种有帮助解决淹没和掩盖问题的方法的特点。在第4节中，我们提供了构建iTrees和iForest的算法。第5节将该方法与三种最先进的异常探测器进行了经验比较；我们还分析了该方法的效率，并在AUC和处理时间方面报告了实验结果。第6节对效率进行了讨论，第7节对本文进行了总结。

2、隔离和隔离树

在本文中，术语隔离是“将实例与其他实例分开”。因为异常现象“少而不同”，因此它们更容易被隔离。在数据诱导的随机树中，实例的划分递归重复，直到所有实例都被隔离。这种随机分区为异常产生了明显的短路径，因为(a)异常实例越少，导致分区数量越少——树结构中的路径越短，而具有可区分属性值的(b)实例更有可能在早期分区中被分离。因此，当一个随机树的森林为某些特定的点共同产生较短的路径长度时，那么它们很有可能是异常的。

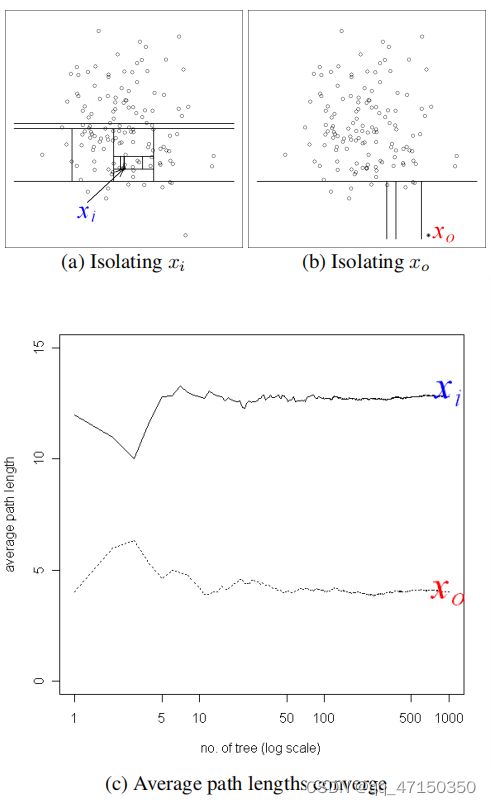
*图1.异常更容易被隔离，因此其路径长度较短。给定一个高斯分布（135个点），(a)一个正态点xi需要有12个随机分区被隔离；(b)一个异常xo只需要4个分区被隔离。当树数增加时，©的xi和xo的平均路径长度收敛。 *

为了证明异常在随机划分下更容易被隔离的观点，我们在图1(a)和1(b)中说明了一个例子，以可视化正常点与异常的运行划分。我们观察到，一个正常的点，xi，通常需要更多的分区来被隔离。异常点xo也相反，它通常需要更少的分区来隔离。在本例中，分区是通过随机选择一个属性，然后在所选属性的最大值和最小值之间随机选择一个分割值来生成的。由于递归分区可以用树状结构表示，因此隔离一个点所需的分区数量相当于从根节点到终止节点的路径长度。在本例中，xi的路径长度大于xo的路径长度。
由于每个分区都是随机生成的，所以将使用不同的分区集生成单独的树。我们在一些树上平均路径长度，以找到期望的路径长度。图1©显示，当树数增加时，xo和xi的平均路径长度收敛。使用1000棵树，xo和xi的平均路径长度分别收敛到4.02和12.82。它表明异常的路径长度比正常实例短。
定义：隔离树。
设T是一个隔离树的一个节点。T要么是没有子节点的外部节点，要么是有一个测试和恰好有两个子节点的内部节点（Tl，Tr）。一个测试由一个属性q和一个分割值p组成，这样测试q < p将数据点划分为Tl和Tr。给定一个样本的数据X={x1，…，xn}n实例d变量分布，建立一个隔离树（iTree），我们递归划分X随机选择一个属性q和分裂值p，直到： (i)树达到高度限制，（ii）|X| = 1或（iii）所有数据X有相同的值。iTree是一个适当的二叉树，其中树中的每个节点恰好有零或两个子节点。假设所有实例都是不同的，当iTree完全增长时，每个实例都孤立于外部节点，外部节点数为n，内部节点数为n−1；iTree的节点总数为2n−1；因此内存需求是有界的，只随n线性增长。
异常检测的任务是提供一个反映异常程度的排名。因此，检测异常的一种方法是根据数据点的路径长度或异常分数对其进行排序；异常是排在列表顶部的点。我们定义路径长度和异常评分如下。
定义：点x的路径长度h (x)是通过从根节点遍历iTree的边数来衡量的，直到遍历在外部节点终止为止。
任何异常检测方法都需要一个异常评分。从h (x)中得到这样的分数的困难在于，虽然iTree的最大可能高度以n的顺序增长，但平均高度以log n [7]的顺序增长。上述任何一项对h (x)的标准化要么没有界限，要么不能直接进行比较。

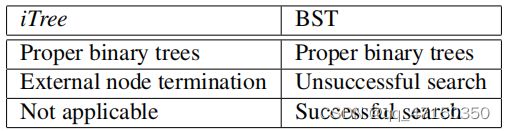
表1.iTree和二进制搜索树（BST）中的等效结构和操作列表

由于iTree具有与二进制搜索树或BST等效的结构（见表1），因此外部节点终止的平均h（x）的估计与BST中的不成功搜索相同。我们借用BST的分析来估计iTree的平均路径长度。给定n个实例的数据集，[9]的10.3.3节给出了BST中不成功搜索的平均路径长度，如下所示：
c(n) = 2H(n − 1) − (2(n − 1)/n), (1)
其中，H (i)为谐波数，可以用ln(i)+0.5772156649（欧拉常数）来估计。由于c (n)是给定n的h (x)的平均值，我们用它来标准化h (x)。实例x的异常分数s被定义为：

其中，E（h(x)）是来自隔离树集合的h (x)的平均值。方程式(2)：
1. when E(h(x)) → c(n), s → 0.5;
2. when E(h(x)) → 0, s → 1;
3. and when E(h(x)) → n − 1, s → 0.
s对于h (x)是单调的。图2说明了E（h(x)）和s之间的关系，以及以下条件，其中0<≤1为0 < h (x)≤n−1。使用异常评分s，我们可以做出以下评估：
(a)如果实例返回的s非常接近于1，那么它们绝对是异常的，
(b)如果实例远小于0.5，那么它们可以被视为正常实例，并且
©如果所有的实例都返回s≈0.5，那么整个样本实际上没有任何明显的异常。
可以通过隔离树集合生成异常评分的轮廓，便于对检测结果进行详细分析。图3显示了这种轮廓的一个示例，它允许用户可视化和识别实例空间中的异常情况。利用该轮廓，我们可以清楚地识别出三个点，其中s≥为0.6，这是潜在的异常。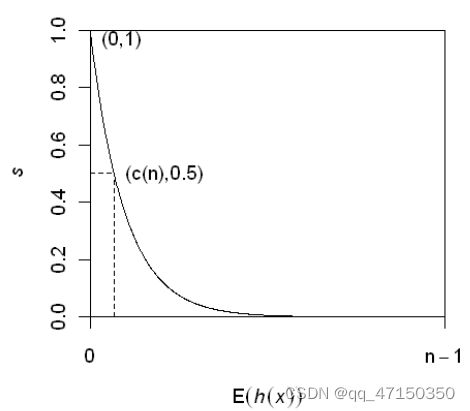
图2。期望路径长度E（h(x)）与异常分数s. c (n)的关系为公式1中定义的平均路径长度。如果预期路径长度E（h(x)）等于平均路径长度c (n)，则s=为0.5，而不管n的值如何。

3、隔离树的特性

本节描述了iTrees的特性，及其处理淹没和掩蔽效应的独特方法。作为一个使用隔离树的树集成，iForest a)将异常识别为具有较短路径长度的点，以及b)有多棵树作为“专家”来针对不同的异常。由于iForest不需要隔离所有的正常实例——大多数训练样本，iForest能够很好地处理部分模型，而不隔离所有的正常点，并使用小样本量构建模型。
与现有的更需要大采样量的方法相反，隔离方法在保持小时效果最好。大的采样量降低了iForest隔离异常的能力，因为正常实例可能会干扰隔离过程，从而降低了其清晰隔离异常的能力。因此，子采样为iForest的良好工作提供了良好的环境。在本文中，我们是通过随机选择不需要替换的实例来进行子抽样的。

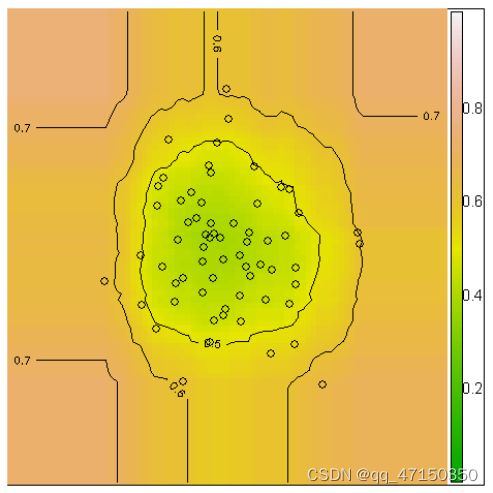
图3.iForest64点高斯分布的异常得分轮廓。说明了= 0.5、0.6、0.6、0.7的等高线。潜在的异常可以被识别为s≥0.6的点。

在异常检测中，对淹没和掩蔽问题进行了广泛研究[8]。淹没指错误地将正常实例识别为异常，当正常实例太接近异常时，分离异常所需的分区数量就会增加——这使得区分异常和正常实例变得更加困难。掩蔽是指存在太多的异常现象来掩盖它们自己的存在。当一个异常集群很大且密集时，它也会增加分区的数量来隔离每个异常。在这种情况下，使用这些树的评估具有更长的路径长度，使得异常更难以检测。注意，淹没和掩蔽都是异常检测过多数据的结果。隔离树的独特特征使得iForest可以通过子采样来建立一个部分模型，这就偶然地减轻了淹没和掩蔽的影响。这是因为： 1)子采样控制数据大小，这有助于iForest更好地隔离异常的例子；2)每个隔离树可以专门化，因为每个子样本包含不同的异常集，甚至没有异常。
为了说明这一点，图4(a)显示了由多交叉生成的数据集。该数据集有两个异常簇，位于中心的一个大的正常点簇附近。数据集有两个异常簇，靠近中心的一大簇正常点。异常簇周围有干扰正常点，在这个4096个实例的样本中，异常簇比正常点更密集。图4(b)显示了128个原始数据实例的子样本。异常簇在子样本中可以清晰地识别出来。围绕这两个异常簇的正常实例已被清除，异常簇的大小变得更小，这使它们更容易以识别。当使用整个样本时，iForest报告的AUC为0.67。当使用128的子采样大小时，iForest的AUC为0.91。结果表明，iForest在通过大量减少的子样本处理淹没和掩蔽效应方面具有优越的异常检测能力。
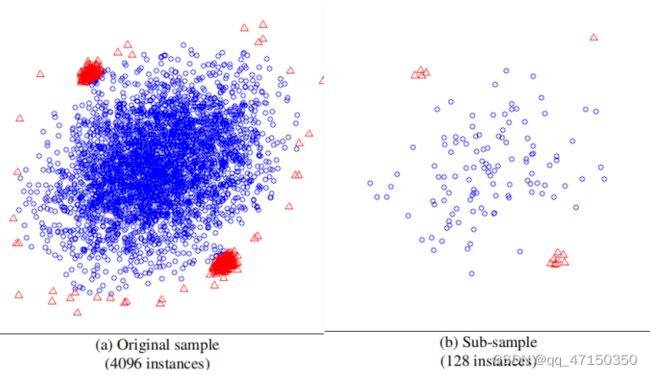图4。使用生成的数据来演示沼泽和掩蔽的效果，(a)显示了由多交叉生成的原始数据。(b)显示了原始数据的一个子样本。圆圈（◦）表示正常实例，三角形(4)表示异常。

4、使用iForest进行异常检测

使用iForest进行异常检测是一个分为两个阶段的过程。第一个（训练）阶段使用训练集的子样本来构建隔离树。第二个（测试）阶段将测试实例通过隔离树传递，以获得每个实例的异常分数。

4.1培训阶段

在训练阶段，iTrees通过递归划分给定的训练集，直到实例被隔离或达到特定的树高，从而得到部分模型。请注意，树高限制l是由子采样大小ψ自动设置的：l = ceiling(log2 ψ)，这大约是平均树高[7]。将树生长到平均树高的基本原理是，我们只对比平均路径长度短的数据点感兴趣，因为这些点更有可能是异常点。训练阶段的细节可以在算法1和算法2中找到。

Algorithm 1 : iForest(X, t, ψ)
Inputs: X - input data, t - number of trees, ψ - sub sampling size
Output: a set of t iTrees
1: Initialize F orest
2: set height limit l = ceiling(log2 ψ)
3: for i = 1 to t do
4: 	X0 ← sample(X, ψ)
5: 	Forest ← Forest ∪ iTree(X0 , 0, l)
6: end for
7: return Forest

Algorithm 2 : iTree(X, e, l)
Inputs: X - input data, e - current tree height, l - height limit
Output: an iTree
1: if e ≥ l or |X| ≤ 1 then
2: 	return exNode{Size ← |X|}
3: else
4: 	let Q be a list of attributes in X
5: 	randomly select an attribute q ∈ Q
6: 	randomly select a split point p from max and min values of attribute q in X
7: 	Xl ← f ilter(X, q < p)
8: 	Xr ← f ilter(X, q ≥ p)
9: 	return inNode{Lef t ← iT ree(Xl , e + 1, l),
10: 	Right ← iT ree(Xr, e + 1, l),
11:		SplitAtt ← q,
12: 	SplitV alue ← p}
13: end if

iForest算法有两个输入参数。它们是子采样大小ψ和树的数量t。我们在下面提供一个指南，为这两个参数选择一个合适的值。子采样大小ψ控制着训练数据的大小。我们发现，当ψ增加到一个期望值时，iForest可靠地检测，不需要进一步增加ψ，因为它增加了处理时间和内存大小，而没有提高检测性能。
经验上，我们发现将ψ设置为2^8即256通常可以提供足够的细节，以便在广泛的数据范围内执行异常检测。除非另有说明，否则我们使用ψ = 256作为我们的实验的默认值。对效应子采样大小的分析可以在第5.2节中找到，其中表明，在这个默认设置下，检测性能接近最优，并且对大范围的ψ不敏感。
树的数量t控制着集合的大小。我们发现路径长度通常在t = 100之前收敛。除非另有说明，我们将在实验中使用t = 100作为默认值。
在训练过程结束时，将返回一组树，并准备好进入评估阶段。iForest训练的复杂性是O（tψ log ψ）。

4.2评估阶段

在评估阶段，从每个测试实例的预期路径长度E（h(x)）中推导出一个异常分数s。E（h(x)）是通过iForest中的每个iTree传递实例导得到的。使用PathLength函数，通过遍历iTree计算实例x从根节点到终止节点的边数e，推导出单路径长度h (x)。当x终止在外部节点时，其中 Size > 1，返回值为e加上调整 c(Size)，此调整涉及到一个超出树高限制的未构建的子树。当对集合的每棵树得到h (x)时，通过计算公式2中的s（x，ψ）得到一个异常分数。评估过程的复杂性为O（ntlog ψ），其中n为测试数据的大小。P长度函数的细节可以在算法3中找到。要找到前m个异常，只需使用s按降序排序数据。前m个实例是顶部的m个异常。

Algorithm 3 : PathLength(x, T, e)
Inputs: x - an instance, T - an iTree, e - current path length;
		to be initialized to zero when first called
Output: path length of x
1: if T is an external node then
2: 	return e + c(T.size) {c(.) is defined in Equation 1}
3: end if
4: a ← T.splitAtt
5: if xa < T.splitV alue then
6: 	return P athLength(x, T.lef t, e + 1)
7: else {xa ≥ T.splitV alue}
8: 	return P athLength(x, T.right, e + 1)
9: end if

5、经验评价

本节详细介绍了旨在评估iForest的四组实验的详细结果。在第一个实验中，我们将iForest与ORCA [3]、LOF [6]和随机森林（RF）[12]进行了比较。LOF是一种众所周知的基于密度的方法，选择RF是因为该算法也使用了树的集成。在第二个实验中，我们使用实验中两个最大的数据集来检验不同子采样大小的影响。该结果提供了一个见解，应该使用什么子采样大小及其对检测性能的影响。第三个实验将iForest扩展到处理高维数据；我们通过对每个子样本应用一个简单的单变量检验，减少了树构造之前的属性空间。我们的目的是找出这个简单的机制是否能够提高iForest在高维空间中的检测性能。在许多情况下，异常数据很难获得，第四个实验在只有正常实例可供训练时检查iForest的性能。对于所有的实验，都报告了实际的CPU时间和曲线下面积（AUC）。它们在Linux集群（www.vpac.org）中以2.3 GHz的速度处理为单线程作业。
基准测试方法是一种基于k-最近邻（k-nn）的方法，是目前最先进的异常检测方法之一，其中对处理时间的最大需求来自于k个最近邻的距离计算。使用样本随机化和一个简单的剪枝规则，ORCA被声称能够将O（n2）的复杂性降低到接近线性时间[3]。
在ORCA中，参数k决定了最近邻域的数量，增加k也增加了运行时间。除非另有说明，我们在以前的实验中使用ORCA的默认设置k = 5。参数Nde终止了报告的异常数量。如果N很小，ORCA就会迅速增加运行截止时间，并减少更多的搜索，从而导致更快的运行时间。由于AUC要求报告每个实例的异常分数，将N设置在异常数以下是不合理的。由于选择N对运行时间有影响，并且在训练阶段异常的数量不应该知道，除非另有说明，我们将使用一个合理的值N =N = n/8。使用ORCA的原始默认设置（k = 5和N = 30），所有大于1000个点的数据集报告的AUC都接近于0.5，这相当于随机选择点作为异常。在报告处理时间时，我们报告了总的训练和测试时间，但省略了ORCA中的预处理时间“dprep”。
对于LOF，我们在实验中使用了一个常用的k = 10的设置。对于RF，我们在其默认值中使用t = 100和其他参数。因为RF是一个监督学习者，我们按照[12]中的精确指令来生成合成数据作为替代类。备选类是通过对所有属性的最大值和最小值之间的随机点进行均匀抽样而生成的。接近度度量是在构建决策树之后计算出来的，异常值是指与数据中所有其他实例的接近度通常很小的实例。
我们使用11个自然数据集加上一个合成数据集来进行评估。之所以选择它们，是因为它们包含已知的异常类作为地面真相，而这些数据集在文献中被用于评估类似环境下的异常检测器。它们包括：KDD CUP 99网络入侵数据的两个最大数据子集（Http和Smtp），用于[14]、甲状腺癌、心律失常、威斯康辛乳腺癌（呼吸）、森林覆盖类型（森林覆盖）、电离层、Pima、卫星、航天飞机[2]、乳房x光检查1和多交叉[10]。由于我们只对连续值属性感兴趣，因此去掉了所有标称属性和二元属性的数据。综合数据生成器，多交叉生成一个多元正态分布与一个可选择的异常簇的数量。在我们的实验中，多交叉的基本设置如下：污染比=10%（总点数上的异常数），距离因子=2（正常团簇中心与异常团簇之间的距离），异常团簇数=2。图4是一个多交叉数据的示例。表2提供了所有数据集的属性和关于体的信息。
假设在训练阶段无法使用异常标签。异常标签仅在评估阶段可用于计算性能度量，即AUC。

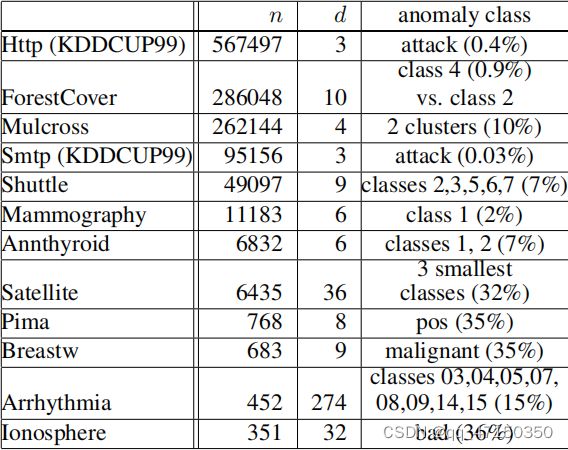
表2.数据属性表，其中n为实例数，d为维数，括号中的百分比表示异常的百分比。

5.1与ORCA、LOF和随机森林的比较

本实验的目的是比较iForest与ORCA、LOF和RF在AUC和处理时间方面的差异。表3报告了所有方法的AUC评分和实际运行时间。从表格中，我们观察到iForest的表现优于ORCA。结果表明，iForest作为一种基于模型的方法，在AUC和处理时间方面都优于基于距离的ORCA方法。特别是，iForest在所有大于1000个点的数据集中更准确、更快。
请注意，iForest和ORCA之间的执行时间差异很大，特别是在大数据集中；这是由于iForest不需要计算成对的距离；尽管ORCA只报告了n/8个异常，其中iForest排名所有n个点，但这种情况还是发生了。
iForest有7个有利于LOF，iFoirest在所有4个数据集中都优于RF。在处理时间方面，iForest在所有数据集上都优于LOF和RF。
iForest的性能在很大范围内稳定。使用最高维数的两个数据集，图5显示了AUC在一个较小的t处收敛。由于增加t也增加了处理时间，AUC的早期收敛表明，如果将t调谐到一个数据集，iForest的执行时间可以进一步减少。
对于Http和Mulcross数据集，由于异常簇的大小较大，并且与正常实例相比，异常簇的密度相等或更高（即掩蔽效应），ORCA报告的这些数据集的结果低于平均值。我们还对ORCA进行了实验，这些数据集使用较高的k值（其中k＝150），但是检测性能相似。这突出了ORCA和其他基于similar k-nn的方法中的一个有问题的假设：它们只能检测小于k的低密度异常簇。增加k可以解决问题，但由于处理时间的增加，在高容量设置中不实用。

表3. iForest的性能有利于ORCA，特别是对于n > 1000的大型数据集。加粗体表示的AUC性能最好。对于包含n > 1000的大型数据集，iForest明显快于ORCA。我们没有LOF和RF的完整结果，因为： (1) LOF具有较高的计算复杂度，不能在合理的时间内完成一些非常高的容量数据集；(2) RF有巨大的内存需求，这需要系统内存（2n）2在无监督学习设置中产生接近矩阵。

图5.检测性能AUC（y轴）收敛于一个小的t（x轴）。

5.2效率分析

本实验研究了iForest的效率与子采样量ψ的关系。利用两个最大的数据集，Http和森林覆盖，我们检验了子样本大小对检测精度和处理时间的影响。在本实验中，我们调整了子采样大小ψ = 2,4,8,16，…，32768。
我们的发现如图6所示。我们观察到，AUC在小ψ时收敛得非常快。当Http的ψ = 128和ψ = 512为森林覆盖时，AUC接近最优，而且它们只是原始数据的一小部分（Http为0.00045，森林覆盖为0.0018）。经过此ψ设置后，AUC的变化最小：分别为±0.0014和±0.023。还要注意的是，当ψ从4增加到8192时，处理时间会增加得非常温和。iForest在这个范围内保持其接近最佳的检测性能。简而言之，一个小的ψ提供了较高的AUC和较低的处理时间，并且不需要进一步增加ψ。

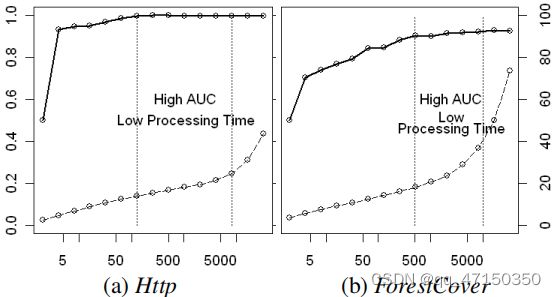
图6。较小的子采样大小可以提供高AUC（左y轴，实线）和低处理时间（右y轴，虚线，单位为秒）。子采样大小（x轴，对数尺度）范围为ψ = 2、4、8、16，…，32768。

高维数据

高维数据是异常检测的重要挑战之一。对于基于距离的方法，每个点在高维空间中都是同样稀疏的——这使得距离成为一个无用的度量。对于iForest来说，它也遭受着同样的“维度诅咒”。
在本实验中，我们研究了高维数据集具有大量无关特征或背景噪声的特殊情况，并表明iForest在处理时间方面具有显著优势。我们使用乳房X光摄影术和Annthy roid数据集模拟高维数据。
对于每个数据集，添加506个随机属性，每个属性均匀分布，值在0到1之间，以模拟背景噪声。因此，每个数据集中共有512个属性。在构造每个iTree之前，我们使用一个简单的统计检验，峰度，从子样本中选择一个属性子空间。峰度衡量的是单变量分布的“峰点”。峰度法对异常的存在很敏感，因此是一种很好的异常检测属性选择器。在峰度为每个属性提供了一个排序之后，根据这个排序选择一个属性的子空间来构建构造每棵树。结果表明，当子空间大小接近原始属性数时，检测性能有所提高。我们还可以选择其他的属性选择器，例如，Grubb的测试。然而，在本节中，我们只关注展示iForest使用属性选择器来降低异常检测任务的维数的能力。
图7显示，a)处理时间仍然小于30秒的整个范围的子空间大小和b) AUC峰值当子空间大小相同的原始属性的数量，这个结果非常接近ORCA使用原始属性。当在两个高维数据集上都使用ORCA时，它报告的AUC接近于0.5，处理时间超过100秒。结果表明，这两个数据集都具有挑战性，但iForest能够通过简单地添加峰度测试来提高检测性能。其他方法很可能应用类似的属性约简技术来提高高维数据的检测精度，但iForest的优点是即使在高维数据中处理时间也较短。

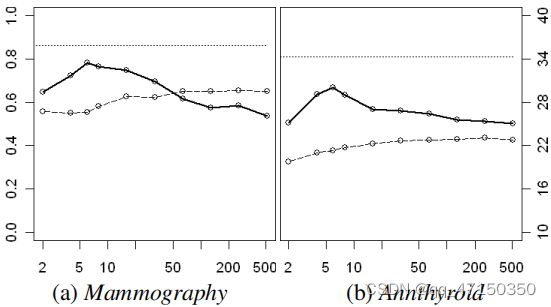
图7. iForest使用峰度选择属性在高维数据上取得了良好的结果，添加了506个不相关的属性。当子空间大小（x轴）接近原始属性的数量和处理时间（右y轴，虚线，以秒为单位）时，AUC（左y轴，实线）略有增加。使用原始数据训练的iForest的AUC略好一些（如顶部虚线所示）。

5.4仅使用正常实例进行培训

当训练集只包含正常实例时，iForest是否可以工作？为了回答这个问题，我们使用实验中两个最大的数据集进行了一个简单的实验。我们首先将每个数据集随机分为两部分，一个用于训练，另一个用于评估，这样AUC就可以基于看不见的数据得到。我们重复这个过程十次，并报告平均AUC。
当有异常和正常点的训练时，Http报告的AUC =为0.9997；然而，当没有异常的训练时，AUC降低到0.9919。对于ForestCover，AUC从0.8817减少到0.8802。虽然AUC有一个小的减少，但我们发现使用一个更大的子采样量可以帮助恢复检测性能。当我们将Http子采样量从ψ = 256增加到ψ=8182，以及ForestCover的ψ = 512和无异常训练时，Http的AUC达到0.9997，森林覆盖的AUC达到0.884。

6、论述

使用小样本的含义是，可以很容易地以最小的内存占用托管在线异常检测系统。使用ψ = 256，最大节点数为511个。设一个节点的最大大小为b字节，t为树的数量。因此，一个检测异常的工作模型估计小于511tb字节，这在现代计算设备中是微不足道的。
iForest在训练阶段的时间复杂性为O（tψ log ψ），在评估阶段为O（ntlog ψ）。对于Http数据集，当ψ = 256、t = 100和评估283,748个实例时，总处理时间仅为7.6秒。我们将子采样大小增加了64倍到ψ = 16384，处理时间仅增加了1.6倍到11.9秒。结果表明，iForest计算复杂度的常数较低。
iForest的快速执行是构建部分模型的直接结果，与给定的训练集相比，只需要一个非常小的样本量。这种能力在异常检测领域是无与伦比的。

7、结论

本文提出了一种完全不同的基于模型的方法，它侧重于异常隔离，而不是正常的实例分析。在目前的文献中没有探讨隔离的概念，隔离的使用在检测异常方面非常有效。利用异常的“少的和不同的”性质，iTree隔离了与正常点相比更接近树根的异常。这种独特的特性允许iForest构建部分模型（而不是在分析中的完整模型），并且只使用一小部分的训练数据来构建有效的模型。因此，iForest具有线性时间复杂度、低常数和低内存要求，这是高容量数据集的理想选择。
我们的经验评估表明，在AUC和执行时间方面，iForest在执行时间方面的表现明显优于基于近线性时间复杂度距离的ORCA、LOF和RF方法，特别是在大数据集中。此外，iForest在较小的集成规模下快速收敛，能够高效地检测异常。
对于包含大量不相关属性的高维问题，iForest可以通过附加的属性选择器快速实现较高的检测性能；而基于距离的方法要么检测性能较差，要么需要更多的时间。我们还证明了即使在训练集中没有出现异常，iForest也可以正常工作。本质上，隔离森林是一种精确和高效的异常探测器，特别适用于大型数据库。它处理高容量数据库的能力对于现实生活中的应用程序是非常理想的。
作者感谢维多利亚先进计算合作伙伴关系（www.vpac.org）提供了高性能的计算设施。Z.-H. Zhou得到了NSFC（60635030,60721002）和江苏（BK2008018）的支持。

参考

[1] N. Abe, B. Zadrozny, and J. Langford. Outlier detection by
active learning. In Proceedings of the 12th ACM SIGKDD
international conference on Knowledge discovery and data
mining, pages 504–509. ACM Press, 2006.
[2] A. Asuncion and D. Newman. UCI machine learning repository, 2007.
[3] S. D. Bay and M. Schwabacher. Mining distance-based outliers in near linear time with randomization and a simple
pruning rule. In Proceedings of the ninth ACM SIGKDD
international conference on Knowledge discovery and data
mining, pages 29–38. ACM Press, 2003.
[4] M. M. Breunig, H.-P. Kriegel, R. T. Ng, and J. Sander.
LOF: identifying density-based local outliers. ACM SIGMOD Record, 29(2):93–104, 2000.
[5] Z. He, X. Xu, and S. Deng. Discovering cluster-based local
outliers. Pattern Recogn. Lett., 24(9-10):1641–1650, 2003.
[6] E. M. Knorr and R. T. Ng. Algorithms for mining distancebased outliers in large datasets. In VLDB ’98: Proceedings
of the 24rd International Conference on Very Large Data
Bases, pages 392–403, San Francisco, CA, USA, 1998.
Morgan Kaufmann.
[7] D. E. Knuth. Art of Computer Programming, Volume 3:
Sorting and Searching (2nd Edition). Addison-Wesley Professional, April 1998.
[8] R. B. Murphy. On Tests for Outlying Observations. PhD
thesis, Princeton University, 1951.
[9] B. R. Preiss. Data Structures and Algorithms with ObjectOriented Design Patterns in Java. Wiley, 1999.
[10] D. M. Rocke and D. L. Woodruff. Identification of outliers
in multivariate data. Journal of the American Statistical Association, 91(435):1047–1061, 1996.
[11] P. J. Rousseeuw and K. V. Driessen. A fast algorithm for the
minimum covariance determinant estimator. Technometrics,
41(3):212–223, 1999.
[12] T. Shi and S. Horvath. Unsupervised learning with random
forest predictors. Journal of Computational and Graphical
Statistics, 15(1):118–138, March 2006.
[13] M. Wu and C. Jermaine. Outlier detection by sampling
with accuracy guarantees. In Proceedings of the 12th ACM
SIGKDD international conference on Knowledge discovery
and data mining, pages 767–772, New York, NY, USA,
2006. ACM.
[14] K. Yamanishi, J.-I. Takeuchi, G. Williams, and P. Milne. Online unsupervised outlier detection using finite mixtures with
discounting learning algorithms. In Proceedings of the sixth
ACM SIGKDD international conference on Knowledge discovery and data mining, pages 320–324. ACM Press, 2000.