集成学习&强化学习及其在群体学习&群体决策中的借鉴意义

在最近的一个项目里强化学习：项目经验汇总，结合集成学习 + 强化学习，实现了图数据中的一个搜索任务。
总结下来，感受到集成学习和强化学习结合在一起，在多个方面展现的独到优势。同时，其中的一些思想和经验，可以反向给予人们一定的借鉴意义，其中群体学习、群体决策方面尤为突出，也尤为有趣。

然而，在调研阶段，并没有检索到集成学习&强化学习两者结合的相关文献资料。

想来，一种可能的主观因素是，调研相对匆忙，检索或许存在一些遗漏；另一种可能的客观因素是，在当前趋之若鹜的深度学习主流背景下，传统模式识别看似缺少所谓“先进性”，却又因其较高的数学基础门槛，较强的技术复杂度，从而整体上导致较低的研究热度，而往往难以见诸于相关期刊会议。

上述为此文相关的大小背景。下文是主要内容细节，个人经验，仅供参考。

1. 集成学习

“三个臭皮匠，赛过诸葛亮”。

不同于以深度神经网络为代表的单一强学习器，集成学习基于“人多力量大的”的思想，将多个（相对）弱学习器组成集群，期望表现出和单一（相对）强学习器相似的效果。集群中的个体，可以称为 “个体学习器” 或者 “基学习器” 。

学习器的相对强弱，指的是完成某种任务能力。例如，某二分类任务，学习器A正确率90%，学习器B正确率60%，则学习器A相对强于B。一般来说，强学习器需要依靠更复杂的模型，付出更多的训练时间，承担更大的发散风险。

按照基学习器之间是“并联”还是“串联”的关系，集成学习可分为两类：

• 并联：bagging，中文一般称为“装袋”
• 串联：boosting，中文一般称为“提升”

Bagging

基学习器之间并联，类似于通过个体投票，得出集群的结论，从而降低估计方差。

代表算法：

• 随机森林（RF）

举个栗子。

【例1】（新）盲人摸象——大象识别

1. 数据采样：四个盲人，分别摸了大象的(1)尾巴、(2)象腿、(3)耳朵、(4)象牙；
2. 个体投票：三个人说：这是大象；其余的一个人说：这不是大象。
3. 群体结论：经过上述投票，群体结论：这是大象。

实际上，这个例子可以看作典型的随机森林算法：每个基学习器随机选取了样本的部分属性，作为相对简单、片面的输入特征。

• 一方面，片面的特征导致信息丢失，将降低了基学习器的识别精度，使其能力相对较弱；
• 另一方面，简单的特征降低了对模型复杂度的要求，使之更易于训练；

Boosting

基学习器之间“串联”，后一个基学习器在前一个基学习器结论的基础上做调整修正，最终得到集群的结论，从而减小偏差。

代表算法：

• AdaBoost(Adaptive Boosting)
• GBDT(Gradient Boosting Decision Tree)
• XGBoost(Extreme Gradient Boosting)

又一个栗子。

【例2】（新）盲人摸象——大象年龄估计

1. 数据采样：四个盲人，依次摸了大象的(1)尾巴、(2)象腿、(3)耳朵、(4)象牙;
2. 个体估计：
   • 第1个人说：我觉得是10岁；
   • 第2个人说：我觉得少了，要加5岁；
   • 第3个人说：我觉得又多了，要再减2岁；
   • 第4个人说：我觉得又少了，要再加1岁；
3. 群体结论：经过上述多次修正，最终结论，大象年龄估计值：10+5-2+1=14（岁）。

值得指出的是，由于Boosting基学习器之间为“串行”结构，前一个基学习器得出结论之后，后一个基学习器才能进行训练，导致基学习器不能并行计算；

相反，Bagging拥有并行训练的优势。

“好而不同”的原则

通过集成学习，可以适当降低基学习器的能力，而通过将所有基学习器整合到一起，使得集群的整体能力达到一定高度。

然而，想要实现“三个臭皮匠，赛过诸葛亮”的效果，这里还需要遵循两个原则，“好，而且不同”。

“不同”的需求

即个体之间的独立性和差异性。直观上，极端情况下，如果个体学习器之间完全相同，则集群的结论和个体的结论也就完全一致，则集群的优势完全没有发挥出来。

换一个角度，在群体的决策过程中，需要有不同的角度、不同的观点、不同的声音。不过需要指出，尽管这些观点可以是片面的、局限的，但是也要保证一定程度的正确性。详细内容参照下一节“好”的度量。

如何保证个体之间的“不同” ？

人是一切社会关系的总和，而个体学习器是其经历的所有数据的总和。

因此，可以通过调整个体学习器拥有不同的“训练经历”，保证其独立和差异性：

• 通过样本抽样的方式，平衡个体学习器训练集之间的共性和差异性；
• 通过属性随机选取，使个体学习器从不同的特征维度（或角度）学习训练；例如随机森林；
• 为个体学习器设计不同的模型；例如混合使用决策树，SVM，不同结构的神经网络等；
• 使用不同的学习方式，使个体学习器以不同的方式进行训练；例如强化学习中，可以分别使用SARSA， DQN等方式训练相同结构的神经网络模型；

“好”的度量

上面提到，在群体的决策过程中，需要有不同的角度、观点和声音，甚至这些声音可以是片面、局限的，即保证个体学习器之间的独立性和差异性。

然而，这些声音也是需要底线的，即保证一定程度的正确性。低于底线的个体将从概率上拉低群体的整体性能。

以一个简单的分类任务为例，说明个体学习器的底线是，个体正确率 $p>50\%$ 。

假设个体学习器之间完全独立不相关，以投票的方式实现集成学习，则群体的正确率可以表示为：

$$P_{ensemble}=\sum _{i>n-i}{C}_n^i{p}^i(1-p{)}^{(n-i)}\dot{=}f(p,n)$$

其中，

• $p$为个体学习器结果正确的概率，$1-p$为其错误概率；
• $n$为个体学习器总个数；
• $i$为结果正确的基学习器个数；
• $C_n^i$表示从$n$个基学习器中，选择$i$个基学习器的有多少种组合方式，即排列组合公式：
  $$C_m^n=\frac{A_m^n}{A_n^n}=\frac{m!}{n!(m-n)!}$$

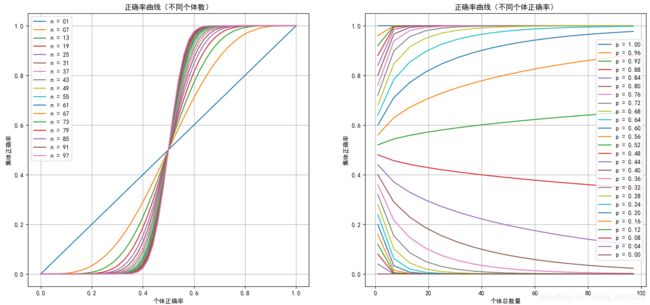
根据上述公式，得到群体投票正确率$P_{ensemble}$和个体学习器结果正确率$p$，以及集群中个体总数$n$，三者之间的关系，绘制为正确率曲线$f(p,n)$如下图（左右其实是一个图），相关代码后附。其中：

• 当集群大小即个体总数$n$固定时，若个体学习器正确概率$p$增加，整体正确率随之增加；
• 当个体学习器结果正确率$p>0.5$时，集群越大，整体正确率越高；
• 当个体学习器结果正确率$p<0.5$时，集群越大，整体正确率越低；
• 当集群大小即个体总数$n$趋于无穷大时：

$$\underset{n\to \infty }{\lim }{P}_{ensemble}=\{\begin{array}{ll}1& \text{if }p>0.5\\ 0.5& \text{if }p=0.5\\ 0& \text{if }p<0.5\end{array}$$

2. 强化学习

简介

这里略过无关细节，仅将与本文主题相关的、实践过程中遇到过的几点问题，做大致说明。

更细节的内容可参考强化学习1：什么是强化学习，收录于专栏《强化学习》(虽然还有很多坑没有填…)，或参考相关书籍资料。

• 强化学习一般用于多步骤、决策类问题；
• 智能体的训练过程，主要为通过在环境中交互试错、迭代进化的过程；
• 智能体的训练目的，是学会对某种局面/状态下，采取某种决定/动作后，将带的总回报进行评估，即对 (状态-动作)对进行价值评估 ，进而以最高价值为决策标准，选择执行的动作；

实践过程中的一系列问题

因此，强化学习实践中可能遇到的问题，或者说影响智能体训练效率的因素主要有（详见强化学习：训练加速技巧）：

1. 模型训练本身，相对监督学习缓慢，且收敛性没有保证；
2. 搜索空间/试错空间庞大，需要大量的试错过程;
3. 经历的积累，由于没有监督数据，只能试错后慢慢积累经历，经历达到一定规模后，才有可能达到训练的最终目的，满足实际需求；
4. 智能体-环境交互，每积累一条经历，便需要一次交互的机会，并进行一次试错，因此大量的交互也会影响训练效率；

实践表明，上述相关问题，可借助集成学习（bagging）的方式化解或缓解。

3. 集成学习&强化学习的结合

这里提到的集成学习，主要指bagging类型，即多智能体并行训练，并行决策，投票汇总。

强化学习问题的解决

模型的弱化和协同训练

通过设计多个智能体作为个体学习器，相比于训练单个智能体，可相对降低智能体的性能要求。具体表现为，使用相对较小的模型，即层数相对较少的神经网络，进而降低单个智能体训练难度，提高收敛性；

另一方面，当多个智能体使用同一套神经网络模型时，智能体之间可通过复制模型参数实现相互学习，实现协同训练：当某智能体在训练期间因为训练不收敛，或者其他原因，导致回报保持相对较低水平时，可以以一定概率向其他表现较好的智能体学习，从而纠正训练的发散，重新从一个“好”的初始状态开始学习；

需要指出的是，上述“当智能体在训练期间出现回报保持相对较低水平时”，不一定是坏的事情，很有可能是探索处于低谷阶段，一定时间后会达到一个更好的状态，因此多智能体协同训练时，需要控制相互学习的概率，对另辟蹊径导致短期表现不佳的智能体，给予更多的宽容和耐心，而不是盲目乐观地向当前最优学习。

试错空间的并行搜索

按照上述协同训练的方式，训练过程中，少部分时间会出现智能体之间的相互学习，而大部分时间是多个智能体独立、并行得展开训练。

因此，多个智能体可以同时对试错空间中的多个区域进行探索，并行试错，并不定期得通过协同训练,将试错经验在整个集群中（隐式地）进行传递；

交互的并行和经历库的共享

对于单个智能体，需要交互、试错达到一定规模，才能够得到相应规模的经历库，作为达到训练目的一个必要需求。

而对于多个智能体的组成的强化学习集群，可并行地实现交互试错，进而通过共同维护、使用同一套经历库，将各自试错经历添加到经历库中，并对经历库中的所有经历拥有读取权限，从而加速经历的积累，提高经历库中内经历的独立不相关性，再反向起到加速每个智能体模型训练的效果；

优势汇总

1. 相比于单一智能体，准确率提高；
2. 学习效率提高，探索效率提高；
3. 训练稳定性提高，训练发散的情况得到抑制；
4. 降低了算力资源限制，对于缺乏GPU算力资源的情况，可考虑通过k8s等建立CPU集群，部署大量智能体副本，实现集成学习和智能体的协同训练。

4. 借鉴意义

群体决策中的“好而不同”原则

人多力量大，但要以相对较高的个体素质水平为前提。

在群体的决策过程中，需要有不同的角度、观点和声音，甚至这些声音可以是片面、局限的，即保证个体学习器之间的独立性和差异性。

但是，这些声音也是需要底线的，即保证一定程度的正确性。从概率角度出发，低于底线的个体将拉低群体的整体决策性能。

群体学习中的两次共享

原始经历的共享

群体的强化学习中，智能体之间共同维护了一套原始经历库，为每个智能体个体提供了更多的、更有差异性的学习素材，从而加速了智能体个体的学习训练。

理想情况下，探索、试错过程中的所有原始经历都值得存档和共享，即便是错误的、过时的、任务相关性弱的，也是非常值得借鉴的经验。横向角度，是群体协作的基础，纵向角度，是群体传承的纽带。

隐式经验的共享

相比于原始经历的“显式”共享，智能体群体的协同训练过程中，“较差”的智能体以一定的概率向“优秀”智能体个体学习，而后者则将其汇总提炼之后的经验，以模型参数的具体形式，“隐式”地实现了共享。

同时，“较差”的个体同样以一定的概率“坚持己见”，对其有一定的包容和耐心，而不扼杀其在未来一段时间里，为群体“另辟蹊径”的可能性。

---

5. 附

bagging群体正确率计算和曲线绘制（Python）

import numpy as np 
import matplotlib.pyplot as plt
from matplotlib import font_manager as fm, rcParams

plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

def choose(num_total, num_select):
    return np.math.factorial(num_total) / np.math.factorial(num_select) / np.math.factorial(num_total - num_select)

def cal_prob_ensemble(p_truth=0.6, num=3):
    n_false = 0
    n_truth = num - n_false
    p_false = 1.0 - p_truth
    prob = 0.0
    while n_false < n_truth:
        prob += choose(num_total=num, num_select=n_truth) * p_truth ** n_truth * p_false ** n_false
        n_false += 1
        n_truth -= 1
    return prob 

if __name__ == "__main__":
    # plt.ion()
    ns = np.arange(1, 101, 6)
    ps = np.linspace(0, 1, 51)
    ys = np.zeros((ns.size, ps.size), dtype=np.float)
    for i, n in enumerate(ns):
        print("n=", n)
        for j, p in enumerate(ps):
            ys[i, j] = cal_prob_ensemble(p_truth=p, num=n)
    
    fig, axs = plt.subplots(1, 2, figsize=(18,8))
    axs[0].plot(ps, ys.T)
    axs[0].set_title("正确率曲线（不同个体数）")
    axs[0].legend(["n = {:02d}".format(n) for n in ns])
    axs[0].set_xlabel('个体正确率')
    axs[0].set_ylabel('集体正确率')
    axs[0].grid()

    axs[1].plot(ns, ys[:, ::-2])
    axs[1].set_title("正确率曲线（不同个体正确率）")
    axs[1].legend(["p = {:1.2f}".format(p) for p in ps[::-2]])
    axs[1].set_xlabel('个体总数量')
    axs[1].set_ylabel('集体正确率')
    axs[1].grid()

    fig.savefig("ensemble_reforcement_learning.png")
    plt.show()