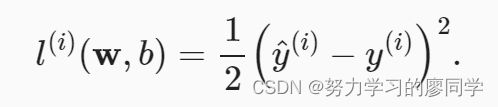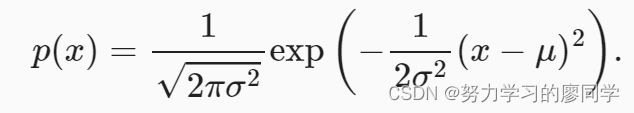动手学深度学习笔记day3

线性回归

线性模型

线性假设是指目标（房屋价格）可以表示为特征（面积和房龄）的加权和，

或其中，x,w∈

 损失函数

  回归问题中最常用的损失函数是平方误差函数。 当样本i的预测值为y^(i)，其相应的真实标签为y(i)时， 平方误差可以定义为以下公式：

 

 为了度量模型在整个数据集上的质量，需计算在训练集n个样本上的损失均值（也等价于求和）。

 在训练模型时，希望寻找一组参数（w∗,b∗）， 这组参数能最小化在所有训练样本上的总损失。

 解析解(线性回归的解)

我们的预测问题是最小化‖y−Xw‖2。 这在损失平面上只有一个临界点，这个临界点对应于整个区域的损失极小点。 将损失关于w的导数设为0，得到解析解：

 随机梯度下降

无法得到解析解的情况下，可以用随机梯度下降方法逼近解析值。

梯度下降（gradient descent）方法：通过不断地在损失函数递减的方向上更新参数来降低误差。

小批量随机梯度下降（minibatch stochastic gradient descent）：梯度下降最简单的用法是计算损失函数（数据集中所有样本的损失均值） 关于模型参数的导数（在这里也可以称为梯度）。 但这必须遍历整个数据集，会非常慢。 因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本， 这种变体叫做小批量随机梯度下降（minibatch stochastic gradient descent）。

在每次迭代中，我们首先随机抽样一个小批量B， 它是由固定数量的训练样本组成的。 然后，我们计算小批量的平均损失关于模型参数的导数（也可以称为梯度）。 最后，我们将梯度乘以一个预先确定的正数η表示学习率（learning rate），并从当前参数的值中减掉。

 注：批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的。 这些可以调整但不在训练过程中更新的参数称为超参数

我们用下面的数学公式来表示这一更新过程（∂表示偏导数）：

 算法的步骤如下： （1）初始化模型参数的值，如随机初始化； （2）从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤。

在训练了预先确定的若干迭代次数后（或者直到满足某些其他停止条件后）， 我们记录下模型参数的估计值，表示为w^,b^。 但是，即使我们的函数确实是线性的且无噪声，这些估计值也不会使损失函数真正地达到最小值。 因为算法会使得损失向最小值缓慢收敛，但却不能在有限的步数内非常精确地达到最小值。

正态分布与平方损失

若随机变量x具有均值μ和方差σ2（标准差σ），其正态分布概率密度函数如下：

def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma**2)
    return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

噪声正态分布如下式:

其中，ϵ∼N(0,σ2)。

均方误差损失函数（简称均方损失）可以用于线性回归。因此，在高斯噪声的假设下，最小化均方误差等价于对线性模型的极大似然估计。

线性回归的从零开始实现

生成数据集

我们将根据带有噪声的线性模型构造一个人造数据集。

def synthetic_data(w, b, num_examples):  
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w))) #生成均值为0，方差为1的size为[1000,2]矩阵
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape) #y=y+噪声
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

读取数据集

训练模型时要对数据集进行遍历，每次抽取一小批量样本，并使用它们来更新我们的模型。要定义一个函数能打乱数据集中的样本并以小批量方式获取数据。

我们定义一个data_iter函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。 每个小批量包含一组特征和标签。

def data_iter(batch_size, features, labels):
    num_examples = len(features)  #矩阵的行数
    indices = list(range(num_examples))  ##用range()函数从0到n-1计数，再通过list()返回列表
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)##随机打乱
    for i in range(0, num_examples, batch_size): 
        ##从0开始，到num_examples结束，每次跳batch_size
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]
    #一个带有 yield 的函数就是一个 generator，
    #它和普通函数不同，生成一个 generator 看起来像函数调用，但不会执行任何函数代码，
    #直到对其调用 next()（在 for 循环中会自动调用 next()）才开始执行
    #可以理解为每次遍历时往features[batch_indices], labels[batch_indices]加入特征，第一次循环为            
    #features[indices[0]
              ...
              indices[batch_size]]

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break  #打断for循环，for i in range(0, num_examples, batch_size): 只执行了一个batch_size

tensor([[ 0.6290,  1.8405],
        [ 1.2323,  0.3050],
        [-0.4671, -1.6299],
        [-0.2333, -0.1458],
        [-0.9337, -0.3508],
        [-0.5376,  0.0201],
        [ 0.7577, -0.1135],
        [ 0.6624, -0.7760],
        [-1.0954,  1.0517],
        [-0.1336, -0.3397]])
 tensor([[-0.8097],
        [ 5.6187],
        [ 8.8130],
        [ 4.2219],
        [ 3.5114],
        [ 3.0744],
        [ 6.1237],
        [ 8.1662],
        [-1.5764],
        [ 5.0715]])

模型设计

#1. 定义初始化模型参数
w = torch.normal(0,0.01,size=(2,1),requires_grad=True)
b = torch.zeros(1,requires_grad=True)
 
#2. 定义模型
def linreg(X,w,b):
  """线性回归模型"""
  return torch.matmul(X,w)+b
 
#3. 定义损失函数
def squared_loss(y_hat,y):
  """均方损失"""
  return (y_hat-y.reshape(y_hat.shape))**2/2

#4. 定义优化算法
def sgd(params,lr,batch_size):#params：参数w和b；lr：学习率；batch_size：批量大小
  """小批量随机梯度下降"""
  with torch.no_grad():  #在该模块下，所有计算得出的tensor的requires_grad都自动设置为False。
#使用了sgd的输出来计算梯度，而不想让梯度去更新sgd的网络参数
    for param in params:
      param -= lr*param.grad/batch_size
      param.grad.zero_() #手动设置梯度清零
 
#5. 训练过程
lr = 0.03
num_epochs = 3 #把整个数据扫三遍
net = linreg
loss = squared_loss
 
for epoch in range(num_epochs):
  for X,y in data_iter(batch_size,features,labels):
    l = loss(net(X,w,b),y)  #l是每个小批量损失
    l.sum().backward() #便于计算梯度,要对参数梯度清零
    sgd([w,b],lr,batch_size) #使用参数的梯度更新参数
  with torch.no_grad():
    train_l = loss(net(features,w,b),labels)
    print(f'epoch{epoch+1},loss{float(train_l.mean()):f}')

epoch 1, loss 0.045372
epoch 2, loss 0.000179
epoch 3, loss 0.000047

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

w的估计误差: tensor([ 0.0005, -0.0004], grad_fn=)
b的估计误差: tensor([0.0013], grad_fn=)

线性回归的简洁实现

  生成数据集

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l 
 
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

读取数据集

调用框架特有的API读取数据，一次读取batch_size个样本。

def load_array(data_arrays, batch_size, is_train=True):   

    """构造一个PyTorch数据迭代器。"""
    dataset = data.TensorDataset(*data_arrays) #将传入的特征和标签作为list传到TensorDataset里面得到一个pytorch的数据集（dataset）
    return data.DataLoader(dataset, batch_size, shuffle=is_train) #调用Dataloader每次从dataset里面挑选batch_size个样本出来（shuffle：是否随机）
 
batch_size = 10
data_iter = load_array((features, labels), batch_size) #将特征和标签传入load_array
 
next(iter(data_iter)) #转化成python的iter，在通过next函数。
#dataloader本质上是一个可迭代对象，可以使用iter()进行访问，采用iter(dataloader)
#返回的是一个迭代器，然后可以使用next()访问。按批次进行的。

[tensor([[ 0.4162, -1.5868],
         [-0.4829,  0.1374],
         [-0.5748, -0.6860],
         [-0.6347,  0.1200],
         [-0.9963,  2.0180],
         [ 1.5813, -1.2615],
         [-0.4949,  2.0363],
         [ 0.3605,  0.5714],
         [ 0.4059, -1.2410],
         [ 0.1744,  1.4118]]),
 tensor([[10.4306],
         [ 2.7637],
         [ 5.3611],
         [ 2.5469],
         [-4.6475],
         [11.6465],
         [-3.7162],
         [ 2.9882],
         [ 9.2429],
         [-0.2496]])]

模型

# `nn` 是神经网络的缩写
from torch import nn
net = nn.Sequential(nn.Linear(2, 1)) #输入维度为2（w），输出维度是1（label） 
#放入sequential容器内，其可以理解为list of layer，层组成的一个list 注：线性回归就一般就是只有一层
 
net[0].weight.data.normal_(0, 0.01) #net[0]表示第0层  .weight访问w  data就是w的值  .normal使用正态分布替换掉data的值
net[0].bias.data.fill_(0) #偏置b置为零

loss = nn.MSELoss()
trainer = torch.optim.SGD(net.parameters(), lr=0.03) #net.parameters()：net里面的所有参数，包括w，b，然后指定学习率

num_epochs = 3  
for epoch in range(num_epochs): #迭代3次
    for X, y in data_iter: #每次拿出一个小批量
        l = loss(net(X), y) #因为net自带参数，所以和之前不同的是不需要再传进去w和b
        trainer.zero_grad() #梯度清零
        l.backward() #pytorch已经计算了sum，计算梯度
        trainer.step() #调用step进行更新
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

epoch 1, loss 0.000392
epoch 2, loss 0.000104
epoch 3, loss 0.000104

文章参考

动手学深度学习