一文讲透系列:在工程应用中使用python做FFT分析
文章目录
- FFT运算应用时的要点
-
- FFT运算前
-
- 数据长度
- 周期情况
- 采样频率
- 数据补零
- FFT运算中
- FFT运算后
-
- 幅值
- 频率
- 相位
- 基于Python的通用化FFT计算函数
- 附录:术语参考
-
- 相干采样和非相干采样
- 分贝dB的定义
本文记录了如何使用scipy提供的FFT函数,实现快速傅里叶变换的实际例程。关于FFT的基本理论,在正文中不会特别介绍,可以根据读者要求,针对特别的知识点在附录中加以说明,本文重点在于介绍如何解决实际工程问题。
很多的教材或文章,都从理论上对快速傅里叶变换(FFT)做了很多的解释和说明,这里不一一赘述,这里有两篇文章可以作为参考阅读资料。第一篇从感性上解释FFT是什么,可以获得什么样的结果,第二篇是一位外国人的视频,硬核推导了FFT算法是如何得到的,基本上看完这两篇FFT就算知道是什么了。
深入浅出的讲解傅里叶变换(真正的通俗易懂)
快速傅里叶变换 (FFT):一个巧妙的算法
但是,懂和会用,是两件事。国内的资料,大部分都在帮助人懂,一旦到了如何用这一步,很多时候就脱节了,这也是为什么国内很多的课程学完了也不知道如何用于实际情况解决相关问题,知其然不知其所以然。真正运用FFT,只要几十行python代码就够了,但是如何根据需要调整这几十行代码,技巧都在纸面外。因此本文首先讲述是“所以然”的内容,在文章的最后一节给出了基于python 3.10 版本的可运行代码,此为通用函数,各位读者可以直接复制使用。
FFT运算应用时的要点
简单来说,FFT运算可以分为运算前,运算中,运算后三个阶段,每个阶段都有一些工程化的要点,而且之间还会相互影响,现分别描述。
FFT运算前
使用前需要考量的内容有,数据长度, 周期情况,采样频率,数据补零。
数据长度
实际工程中,数据来源可以分成两种,真实物理系统获得的采样值(如振动传感器,通信接收器上的电压信号,图像传感器的像素值等),以及仿真系统获得的仿真数据。前者数据量可以认为无穷尽,后者是根据仿真的约束条件,生成的可控长度数据,但即便可控,数据长度可能也会很长。理论上,FFT的数据长度可以非常长,但是长度越少,所需运算时间越长,因此,第一个需要解决的工程化问题就是分析数据的长度。
解决方案很简单,把数据截成等长的一段一段的,每段的长度记为 N f f t N_{fft} Nfft,对每一段数据做FFT,然后可以分别显示每一段的处理结果,也可以将每一段的处理结果加在一起做平均,用平均值来作为最终的处理结果。
这样,无论数据有多长,都可以将其拆成运算时间可接受的小段数据处理。
周期情况
输入的数据(即“信号”)可能是周期的,也可能是非周期的。周期信号容易处理,可以将截断的长度就放在一个完整周期长度左右,这样就可以从FFT的结果里获得相应的频率信息。但是针对非周期信号,简单的截断会给FFT的计算带来一个问题,频率泄露。
频率泄露是指原本在输入频率的幅值会被降低,而不存在于输入信号中的频率点会有幅值存在,从幅频图上“形象”的认为,分析结果从已存在频率“泄露”到了不存在的频率点上。如下图,红色是没有频率泄露时,绿色是存在频率泄露时。
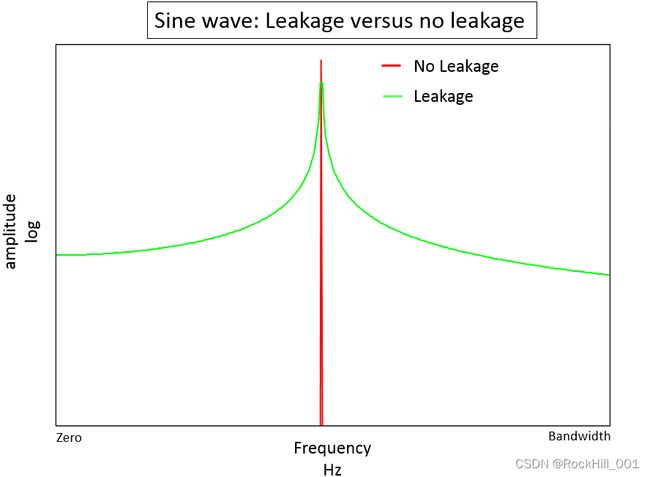 FFT过程认为将被运算的数据无限幅值延拓后,就是原信号,所以如果截断是基于信号的周期是不会有频率泄露的,因为延拓后的信号确实等于原信号,但是如果截断的数据是非周期的,延拓后不等于原信号,则频率泄露是实际发生的。这种非周期的情况,既可以是用非周期的长度截取了周期信号,也可以是信号本身就是非周期的,二者均会发生频率泄露。解决此问题的方案是加窗,尤其是非周期信号,加窗是必须项。
FFT过程认为将被运算的数据无限幅值延拓后,就是原信号,所以如果截断是基于信号的周期是不会有频率泄露的,因为延拓后的信号确实等于原信号,但是如果截断的数据是非周期的,延拓后不等于原信号,则频率泄露是实际发生的。这种非周期的情况,既可以是用非周期的长度截取了周期信号,也可以是信号本身就是非周期的,二者均会发生频率泄露。解决此问题的方案是加窗,尤其是非周期信号,加窗是必须项。
加窗,简单来说,是用特殊的函数来截断数据,使得数据和函数相乘后,其结果为周期化的,减少频率泄露。常见的窗函数有以下几种。其中Uniform窗,即是简单截断,汉宁窗为比较常用的窗函数。
- 统一窗函数(uniform)
- 汉宁窗(Hanning)
- 海明窗(Hamming)
- 布莱克窗(Blackman)
- 平顶窗(Flattop)
- 凯撒窗或凯撒贝塞尔窗(Kaiser-Bessel)
关于窗函数和频率泄露,可以参考以下几篇文章
怎样用通俗易懂的方式解释窗函数?
Windows and Spectral Leakage
什么是泄漏
此外,使用窗函数,可以解决频率泄漏问题,但是也会导致信号丢失,这种丢失可以表现在两个方面,信号幅值的丢失,以及信号能量的丢失。每种窗都存在固定的补偿系数,可以在FFT运算结果上乘以补偿系数,将幅值补偿为原值或者将能量补偿为原值,两种补偿只能选择一种,不能同时选择。下表列出了不同窗的补偿系数。
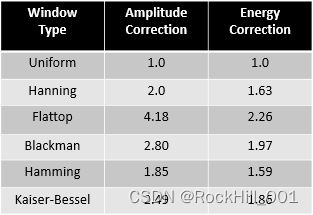
需特别说明,补偿不是必须项,如果只是观察频率的分布情况,而不需要考虑器幅值的具体数值,可以不直接使用Uniform窗(即不加任何窗,直接截断),只有需要考察幅值或者能量的数值时,才需要考虑加窗后的补偿
关于加窗后的补偿,可以参考下文做进一步的了解
Window Correction Factors
采样频率
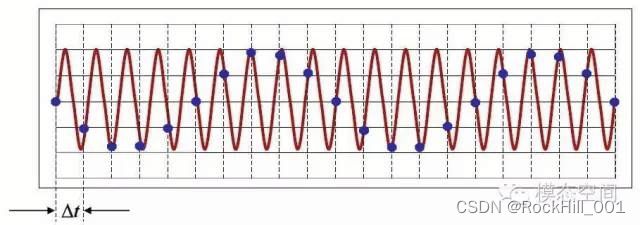
根据奈奎斯特采样定理,需要至少两倍于信号频率的采样频率,才可以正确还原出信号频率,否则会发生频率混叠。当采样频率设置不满足采样定理,即采样频率少于2倍的信号频率时,会导致原本的高频信号被采样成低频信号,如下图所示。红色信号是原始的高频信号,但是由于采样频率不满足采样定理的要求,导致实际采样后的数据点如图中蓝点所示,将这些蓝点连成曲线,可以明显的看出这是一个低频信号。在图示的采样时间长度内,红色信号有18个周期,但采样后的蓝色信号只有2个周期。也就是采样后的信号频率成分为原始信号频率成分的1/9。就是所谓的混叠。对连续信号进行等间隔采样时,如果采样频率不满足采样定理,采样后信号的频率会发生混叠,即高于奈奎斯特频率的频率成分将被重构成低于奈奎斯特频率的频率成分。这种现象导致的失真称为混叠,也就是高频信号被混叠成了低频信号。
因此采样频率 F s F_s Fs决定了分析结果中最高的频率值( F s 2 \frac{F_s}{2} 2Fs)。采样频率的一半称为奈奎斯特频率,也称为分析带宽,简称为带宽。
如果信号中没有高于奈奎斯特频率的频率成分,则不存在混叠,现实世界中的信号很难保证满足这一点。如果采样频率极高也可以一定程度上避免混叠,但这并不总是实用和可能,因为,最高采样频率受数采设备的限制,同时,当采样频率过高时,会出现大的数据文件。另外,采样定理只保证了信号不被歪曲为低频信号,但不能保证不受高频信号的干扰,如果传感器输出的信号中含有比所需信号频率还高的频率成分,ADC同样会以所设采样频率加以采样,混入分析带宽之内。
所以,采样前应把比关心信号的最高频率成分以上的频率滤掉,这就是通常说的抗混叠滤波。它是一个低通滤波器,低于奈奎斯特频率的频率通过,移除高于奈奎斯特频率的频率成分,这是理想的滤波器。实际情况是任何滤波器都不是理想的滤波器,抗混叠滤波器也不例外。滤波器存在滤波陡度,在滤波截止频率(奈奎斯特频率)以上的一些区域还存在混叠的可能性,这个区域对应带宽80%以上部分,即带宽的80%-100%区域。如下图所示,高于奈奎斯特频率以上的频率成分会关于奈奎斯特频率镜像到带宽的80%~100%区域,形成混叠,而带宽80%以内的区域,是无混叠的。

如果希望整个关心的频率范围内都不存在混叠,那么,采样频率要满足: f s ≥ 2.5 ∗ f m a x f_s \geq 2.5* f_{max} fs≥2.5∗fmax。 式中, f m a x f_{max} fmax是关心的最高频率。这就使得可能存在频率混叠的区间位于感兴趣的频宽之外了。如要求100Hz内无混叠,则采样频率应设置成250Hz,带宽为125Hz,带宽的80%为100Hz,因此,可能存在混叠的带宽80%以上区域已位于感兴趣的频带之外了。当采样频率高于关心的最高频率2.5倍时,关心的频带内已无混叠了。另一方面,快速傅立叶变换要求处理的数据块包含的数据点为 2 N 2^N 2N个,而计算机也只能用0和1来存储数据,因此,计算机处理数据时,如果点数是 2 N 2^N 2N个会更快捷些。我们知道 ,因此,离2.5最近的2.56便成为了一个重要的“优先数”(先借用一下优先数这个概念)。基于以上两个方面的原因,采样频率从定理中的2倍提高到工程上的2.56倍。也就是说当采样频率高于关心的最高频率的2.56倍时,关心的最高频率以内的带宽是无混叠的。因此以上的公式调整为工程化的方案 :
f s ≥ 2.56 ∗ f m a x f_s \geq 2.56* f_{max} fs≥2.56∗fmax
但是要注意,这还是从频率上去定义采样频率的,如果按2.56倍设置采样频率,虽然频率没有混叠,但可能信号的幅值还存在失真。那么,如果希望信号的幅值不失真,采样频率应该设置多高才合理呢? 当关心频率成分时,可以按2.56倍的关系设置采样频率;但如果关心信号的幅值(时域),那样,采样频率应设置成关心的最高频率的10倍以上,才不会使信号幅值有明显的失真。
数据补零
有时需要对数据的尾部做补零处理,原因有两个。
第一个原因,FFT要求待处理的数据块包含的数据点需为 2 N 2^N 2N个,有时数据量不足 2 N 2^N 2N个,需要在数据块尾部直接补“0”,使得数据长度满足 2 N 2^N 2N。
第二个原因,为了提高计算结果的频率分辨率。存在两种类型的频率分辨率,一种叫波形分辨率,其由原始数据的时间长度决定,
Δ R ω = 1 T \varDelta R_\omega=\frac{1}{T} ΔRω=T1
另一种可以称之为显示分辨率或FFT分辨率,其由采样频率 F s F_s Fs和参与FFT的数据点数 N f f t N_{fft} Nfft决定
Δ R f f t = F s N f f t \varDelta R_{fft}=\frac{F_s}{N_{fft}} ΔRfft=NfftFs
补零可以提高后一种分辨率,避免栅栏效应。所谓栅栏效应,是指在对信号离散化处理后,得到的是对应采样点的数值,两个采样点之间的数值会无法显示,仿佛是透过栅栏看向外部。这个现象在时域和频域都会存在,在频域尤其明显。这里可以用一个例子说明。
有一个最高频率f = 32kHz的模拟信号,采样频率 64kHz,对这个信号做一个16个点的FFT分析,采样点下标 n 的范围是0, 1, 2, 3, …, 15。那么64kHz的模拟频率被分成了16份,每一份是4kHz,这个4kHz被称为频率分辨率。
所以,频率图的横坐标中:
n=1 对应的f是4kHz
n=2 对应的f是8kHz
…
n=15 对应的f是60kHz
而频谱是关于n=8对称的,只需关心n = 0 ~ 7的频谱就足够了。因为,原信号的最高频率是32kHz。
此例子中,频率分辨率即为 64 k H z / 16 = 4 k H z 64kHz/16=4k Hz 64kHz/16=4kHz,也即每个栅栏的宽度为4k Hz,如果信号的频率落在了两个栅栏之间(例如3.5k Hz),则在画图显示时,无法直观看到真实的频率点位置,而是在4kHz处有个高峰,带来了显示的误差。此时可以通过增加数据点数 N f f t N_{fft} Nfft来提高显示分辨率,例如将上例中的16个点变为32个点,则显示分辨率就变成了2k Hz,而为了能够正确显示3.5k Hz的频率,可以选择视觉分辨率到0.5k Hz,此时点数为128个。对于这些增加出来的点数,全部可以通过在对数据尾部补“0”来到指定个数来实现。需要说明的是,补零不能提高第一种分辨率,提高第一种分辨率,必须增加真实的采样点数才可以做到。
关于分辨率的说明,可以参见此文章,上述的一些内容也都引用于此文章。
补零、频谱泄露、栅栏效应的关系
FFT运算中
在FFT运算中,如果是分析既有的采样数据,可以
- 根据根据采样频率,得到奈奎斯特频率,即带宽
- 根据分析的最小频率间隔,确定数据的最小长度
- 如果数据长度不为2的幂次,可以用补零将其补齐
- 如果数据为非周期信号或者无法调整数据长度得到相干采样(见附录)的结果,那么需要使用适当的窗函数
- 如果只是分析频率分布,在使用窗之后无需补偿,否则,需要选择幅值补偿或者能量补偿
- 如果数据较长且非周期,可以加窗截断后分段处理
如果数据是来自于仿真模型,即数据的生成可控,则可以根据目的,适当调整数据的生成,以满足上述列表里的目标。
FFT运算后
FFT运算后,得到的数据是一组复数数组,其数据个数等于输入数据的个数 N f f t N_{fft} Nfft,该数组的第一个数据对应的是频率为0的幅值,即直流分量,其余的元素,以第 N f f t 2 \frac{N_{fft}}{2} 2Nfft个元素为中心,对称存在,即第2个元素与第 N f f t − 1 N_{fft}-1 Nfft−1个元素相同。要得到正确的频率和幅值数据,需要对FFT结果做相应的处理
幅值
首先得到全部复数其对应的模值,然后再将其归一化处理,其中
0Hz对应幅值 = 当前值 / 采样点数
其余频率对应的幅值 = 当前值 /(采样点数 / 2)
对于幅值处理,可以考虑直接原始数据显示,也可以考虑用对数坐标的方式,或者转化为dB,关于dB的使用,参见附录中的内容
频率
首先截取[0, N f f t 2 \frac{N_{fft}}{2} 2Nfft]的序列,注意包含左右两个端点的数值,其次将每一个序号乘以显示分辨率 F s N f f t \frac{F_s}{N_{fft}} NfftFs,得到的就是频率范围。
相位
直接计算每个复数的角度就是相位,由FFT结果对称性可知,相位也是对称的。
关于对FFT运算后的结果处理,可以参见以下文章
如何 FFT(快速傅里叶变换) 求幅度、频率
基于Python的通用化FFT计算函数
import numpy as np
from numpy.fft import fft
def fft_calc(x, f_s, x_size, nfft):
w = np.hanning(nfft) # 加汉尼窗
cnt = x_size // nfft # 计算数据长度可以覆盖几个窗口
# 将输入数据长度补齐为窗口长度的整数倍,补齐数据为0
# 此方式可以避免输入数据长度小于窗口长度
if cnt == 0: # 用0在数据尾部补齐
x_pad = np.pad(x, (0, nfft - x_size))
else:
x_pad = np.pad(x, (0, x_size - cnt * nfft))
cnt = len(x_pad) // nfft # 更新补齐的数据长度可以覆盖几个窗口
# 以窗口长度计算输入数据的FFT
tmp = []
for i in range(cnt): # 窗与窗之间数据不重叠
p = fft(w * x_pad[i * nfft:(i+1) * nfft]) # 计算加窗的FFT并乘以调整系数
tmp.append(p) # 每个窗的结果
# 将所有计算取平均值
fft_result = np.mean(tmp, axis=0) # 将所有窗平均得到最终结果
# 根据采样宽度计算幅值
amp = abs(fft_result)*2 / (nfft / 2)
# 对直流分量额外调整
amp[0] /= 2
# 根据FFT特性,取一半频谱即可
amp_half = amp[:int(len(amp) / 2)+1]
# 根据采样频率和采样点数,计算频率分辨率,并得到对应的频率坐标
freq = np.arange(int(len(amp) / 2)+1) * f_s/nfft
return amp_half, freq
以下是使用该函数的例程
import numpy as np
from matplotlib import pyplot as plt
pi = np.pi # 圆周率
fs = 1000 # 采样频率
dt = 1/fs # 采样周期
f1 = 10 # 信号的特征频率1
f2 = 100 # 信号的特征频率2
f3 = 200 # 信号的特征频率3
N = 2**12 # 离散信号的长度
tn = np.arange(0, dt*N, dt) # 时间序列
x = 2*np.cos(2*pi*f1*tn) + 2*np.cos(2*pi*f2*tn) + 2*np.cos(2*pi*f3*tn) # 生成离散信号
nfft = fs # FFT的窗长
(amp, freq) = fft_calc(x, fs , N , nfft)
# plot for FFT
fig = plt.figure(figsize=(12, 8))
plt.plot(freq, amp, color="blue")
plt.title('FFT result')
plt.xlabel('Freq /Hz')
plt.ylabel('urad/Hz')
# plt.xscale('log')
ax = plt.gca()
plt.grid(which='both', axis='both')
plt.show()
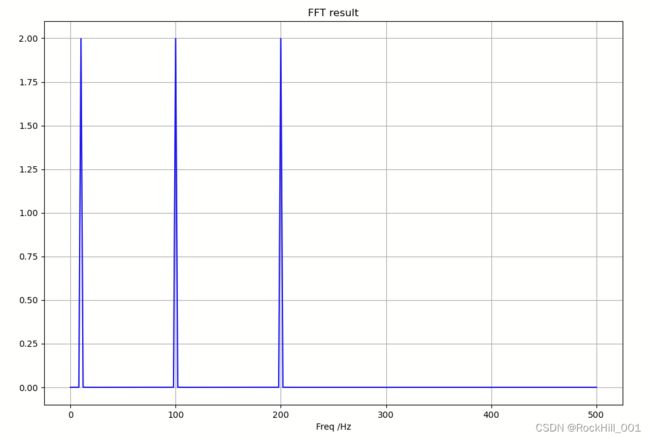
运行后结果如下,注意三个频点与生成的信号一致,幅值都为2,数据总长度为4096个点,窗口宽度与fs保持一致。(python的fft运算可以使用非2的幂次数据长度,此外如果窗口宽度不是采样频率的整数倍,会出现幅值异常,原因未知)
附录:术语参考
相干采样和非相干采样
采样是数字信号处理中的重要概念,它包含两方面内容,简单的说就是抽取和截断!抽取就是时域连续的模拟信号按照采样频率进行等间隔提取,所谓截断就是对时域无限长的模拟信号只取一段时间进行处理。经过抽取和截断后,我们就将模拟信号变成数字信号(这里暂不考虑量化)。
对于周期信号,相干采样(Coherant Sampling)就是采样频率与输入信号频率之比为有理数(整数或是分数),反之则为非相干采样(Incoherant Sampling)。对于非周期信号,由于输入信号没有周期,就没有相干采样和非相干采样的概念。周期信号,如果使用非相干采样,当进行FFT频谱分析时,会发生频率泄露(Spectral Leakage)
分贝dB的定义
dB不是一个单位,是个无量纲。最初是在电信行业使用,为了量化长导线上传输电报和电话信号时的功率损失而开发出来的。
分贝dB定义为两个数值比率的对数值,这两个数值分别是测量值和参考值(也称为基准值),存在两种定义
一种是功率之比: 1 d B = 10 log 10 ( W W 0 ) 1dB=10\log_{10}(\frac{W}{W_0}) 1dB=10log10(W0W)
一种是幅值之比: 1 d B = 10 log 10 ( X X 0 ) 2 = 20 log 10 ( X X 0 ) 1dB=10\log_{10}(\frac{X}{X_0})^2=20\log_{10}(\frac{X}{X_0}) 1dB=10log10(X0X)2=20log10(X0X)
常见的参考值如下
| 幅值之比 | 功率之比 | ||
|---|---|---|---|
| 信号类型 | 参考值 | 信号类型 | 参考值 |
| 位移 | 1 ∗ 1 0 − 12 1*10^{-12} 1∗10−12 m | 声功率 | 1 ∗ 1 0 − 12 1*10^{-12} 1∗10−12 W |
| 速度 | 1 ∗ 1 0 − 9 1*10^{-9} 1∗10−9 m/s | 声功率 | 1 ∗ 1 0 − 12 1*10^{-12} 1∗10−12 W/ m 2 m^2 m2 |
| 加速度 | 1 ∗ 1 0 − 6 1*10^{-6} 1∗10−6 m/ s 2 s^2 s2 | ||
| 声压 | 2 ∗ 1 0 − 5 2*10^{-5} 2∗10−5 Pa |