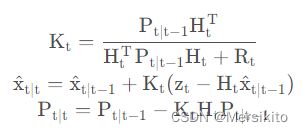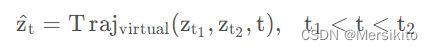【论文阅读4】Observation-Centric SORT：Rethinking SORT for Robust Multi-Object Tracking
【论文阅读4】Observation-Centric SORT：Rethinking SORT for Robust Multi-Object Tracking
1. 各部分笔记
1.1 Abstract
现有的MOT方法，如SORT，它使用Kalman滤波估计目标的运动。由于 标准Kalman滤波基于线性运动假设（即假设目标在相邻两帧之间的运动近似为线性），其更适用于高帧率视频。因此这些运动模型对 遮挡、非线性运动、低帧率视频 的情况并不鲁棒。
OCSORT尝试 优化运动模型（即Kalman滤波），并强调了 检测结果（Observation，观测） 对恢复丢失的轨迹和减少丢失期间线性运动模型的误差累积的作用，提高了对遮挡和非线性运动等情况的鲁棒性。
1.2 Introduction
本文的目标：开发一种 基于运动模型的MOT方法，该方法对遮挡和非线性目标运动具有鲁棒性。
本文的动机：遮挡或非线性运动情况下的大多数错误都是由基于线性运动假设的运动模型引起的。与目标检测和Re-ID相比，运动模型的研究相对较少。通过解决线性运动模型在MOT中的局限性，可以在没有其他线索（如外观特征）的情况下获得最先进的跟踪性能。
当Kalman滤波的状态估计不可靠时，不以估计值为中心，而以检测结果（观测值）为主要信息，可以提高Kalman滤波的鲁棒性。
SORT的三个局限性：
- Kalman滤波状态估计对噪声敏感：尽管目标在高帧率视频相邻两帧之间的运动可以近似为线性，但高帧率也会放大对状态噪声的敏感。在高帧率视频的连续帧之间，目标位移的噪声可能和位移大小本身差不多（因为目标在相邻两帧之间的位移会很小），这导致Kalman滤波对速度的估计的方差会变得很大。
- Kalman滤波状态估计的误差随时间累积：由于遮挡或非线性运动，当Kalman滤波更新没有可用的观测时，目标状态噪声可能会进一步累积。本文证明了在这种情况下，Kalman估计物体位置的误差积累与时间成平方关系。
- 以估计为中心：SORT主要依赖于Kalman状态估计，仅将观测值（检测结果）作为辅助信息。作者认为现在的检测器足够强，应该把观测值作为主要信息（Observation-Centirc的来源）
针对以上三个问题，作者提出了三个创新：
-
提出了以观测为中心的在线平滑（OOS）策略，来减少由于没有新的观测与现有轨迹匹配时导致的Kalman估计的误差积累。
具体来说就是：当一个inactive的轨迹在untracked一段时间后再次与观测相关联时，先为该目标构建一条虚拟轨迹。虚拟轨迹的起始为其untracked前最后一次匹配的观测，终止为其重新匹配的观测。在这两个位置之间平滑KF参数，以获得更好的位置估计。
-
在cost matrix中加入轨迹的方向一致性，以便更好地匹配轨迹和观测。设计的动机是线性运动假设中的轨迹动量，因此称之为以观测为中心的动量（OCM）。证明了：用大时间间隔估计两点之间的方向可以降低对噪声的敏感性。
-
为了处理目标在短时间间隔内由于遮挡而没有被跟踪到（inactive）的情况，通过将其上一次匹配的观测与最新的观测相关联来恢复被中断的轨迹，称之为以观测为中心的恢复（OCR）
1.3 Kalman滤波
对于线性，高斯的问题，我们要对目标的状态进行估计。我们已经假设一个线性模型，以及有一个外部的检测器可以对目标的状态进行观测(Observation)。Kalman滤波要解决的问题是，如何结合我们假设的运动模型和观测值，更好地对目标的状态进行估计。
1.4 Rethinking SORT
1.4.1 Background
SORT中KF的状态变量有7维，即：
各部分含义如下：
| 状态变量 | 含义 |
|---|---|
| u u u | 中心点x坐标 |
| v v v | 中心点y坐标 |
| s s s | 面积 |
| r r r | 长宽比(通常为常数) |
| u ˙ \dot u u˙ | x方向速度 |
| v ˙ \dot v v˙ | y方向速度 |
| s ˙ \dot s s˙ | 面积变化率 |
SORT的线性模型是不含输入的，只有从过去状态到现在状态的估计。因此根据第2部分推导的Kalman滤波，预测步骤为：
更新步骤为：
预测步骤与更新步骤循环进行，以上即为论文的(1)(2)式。
论文的(3)式应该是有点问题的，转换矩阵的形式应该不是那样，起码第四行应该是 [ 0 , 0 , 0 , 1 , 0 , 0 , 0 ] [0,0,0,1,0,0,0] [0,0,0,1,0,0,0]。
对于检测器的观测来说，通常包含五个状态变量：中心点坐标、长宽和置信度, 记为 z = [ u , v , w , h , c ] T z = [ u , v , w , h , c ]^{\Tau} z=[u,v,w,h,c]T
一般来说，当视频帧速率较高时，SORT在跟踪非线性运动目标的场景下（例如跳舞、击剑、摔跤）也能很好地工作。这是因为目标的运动可以很好地近似为短时间间隔内的线性运动。
1.4.2 SORT的三个局限性
1.4.2.1 Kalman滤波状态估计对噪声敏感
证明Kalman滤波对速度的估计的方差会变大，对噪声敏感。
所以说，对速度的估计实际上把原有的方差放大了。
在大多数情况下，这不会对一个时间步长产生大的影响，因为即使线性模型预测的位置有问题，也可以通过观测来校正。但当Kalman滤波更新没有可用观测时，多个时间步长的误差会累积。
1.4.2.2 当Kalman滤波更新没有可用的观测时，误差积累与时间成平方关系
1.4.2.3 以Kalman状态估计为中心
作者认为检测器的性能已经足够好，以至于可以保证 观测的方差小于Kalman状态估计的方差。
1.5 OC-SORT的三个改进
1.5.1 以观测为中心的在线平滑（OOS）
OOS为了解决：当一个inactive的轨迹在untracked（没有可用的观测）一段时间后再次与观测相关联时，如何减少误差的累积。
具体的做法是构建一条虚拟轨迹，虚拟轨迹的起始为其untracked前最后一次匹配的观测，终止为其重新匹配的观测。以往的算法是直接根据当前的观测来预测，然而作者做的是结合当前的观测和最后一次匹配的观测做一个平滑。
设untracked前最后一次匹配的观测为 Z t 1 Z_{t_1} Zt1，重新匹配的观测为 Z t 2 Z_{t_2} Zt2，则虚拟轨迹可以表示为：
论文(7)式
在实现中，作者也是使用恒定速度假设来构建这条虚轨迹。根据匀速运动模型 x ( t ) = x ( t 0 ) + v ( t − t 0 ) x(t)=x(t_0)+v(t−t_0) x(t)=x(t0)+v(t−t0)，有：
论文(10)式
代入Kalman的更新的式子，可以得到：
这里有一个问题，在untracked目标被再次发现以后，通过建立虚拟轨迹来对再次发现后的状态做一个修正。文中说"Given the supervision of the virtual observation trajectory, error raised in state estimation would not be accumulated any more", 但是没有给出证明。
1.5.2 以观测为中心的动量(OCM)
大多数MOT方法在建立cost matrix的时候基本依据两点：运动特征和外观特征。
线性运动模型假设一致的速度方向。然而，由于物体的非线性运动和状态噪声，这种假设往往不成立。在相当短的时间内，我们可以将运动近似为线性，但噪声仍然阻止我们利用速度方向的一致性。我们提出了一种降低噪声的方法，并将速度方向一致性（动量）项添加到代价矩阵中：
其中
表示Kalman滤波的状态估计，
表示观测，
表示速度的方向。
作者在附录证明了，在估计方向时取的时间间隔越大, 方差就会越小。
1.5.3 以观测为中心的恢复(OCR)
一旦一条轨迹在正常关联阶段之后仍然没有被匹配成功，我们尝试将这条轨迹的最后一次观测与当前帧最新的观测进行关联，来恢复被中断的轨迹。
