通过深度神经网络实现可扩展性因果图学习
通过深度神经网络实现可扩展性因果图学习
-
- 写在前面
- 背景介绍
- 相关方法
-
- Granger Causality
- Transfer Entropy
- Graph Learning
- Kernel-based Methods
- Supervised Learning Methods
- MLP and LSTM
- Graphical Neural Network
- 模型概述
-
- 模块 1:学习变量内非线性
- 模块 2:因果图学习(重点)
- 模块 3:学习变量间非线性
- 模块 4:回归预测
- 实验部分
-
- 对比方法
- 数据集设置
- 实验结果
写在前面
这是一篇CIKM(B类)2019年的论文,用神经网络做因果图学习,和我的研究方向相关,因此做一下笔记。
太长不看版:
输入: m × n m\times n m×n的矩阵,表示 m m m个变量的 n n n步时序列
输出: m × m m\times m m×m的矩阵,表示各变量之间的关联程度(包含非线性)
思想:通过时序预测做自监督训练
过程:
- 向网络输入 m × l m\times l m×l的矩阵,l表示预测需要的时序长度
- 通过改版的ResNet,得到多层 m × p m\times p m×p的矩阵,表示单节点非线性变量
- 各矩阵转置经过 m × k , k × k , k × m m\times k, k \times k, k \times m m×k,k×k,k×m的矩阵,得到多个考虑不同变量影响的变量 m × p m\times p m×p
- 将各矩阵拼接在一起,通过MLP得到 m × t m\times t m×t的多节点非线性变量,再通过一个相同维度的 R R R模拟回归系数,然后做点积,得到预测结果
- MSE作为 l o s s loss loss并反向传播更新参数
- 训练结束后3中的三个矩阵相乘作为近似的关联矩阵
论文PDF链接
背景介绍
复杂系统中的因果图学习是非常重要的。现有的方法主要聚焦的是基于预先设定的核或者数据分布而做的因果图学习(也就是说需要具备一定的领域知识),或者只研究了系统中特定的单个目标对剩余节点的影响。同时,现有方法大多只能对线性因果关系进行发掘。而数据的非线性性会给因果图学习带来较大的影响,使得现有方法失效。
从数学上来说,因果图学习的输入是 X = { X ( 1 , ∗ ) , X ( 2 , ∗ ) , . . . , X ( m , ∗ ) } ∈ R m × n X=\{X(1, *), X(2, *),...,X(m,*)\}\in\mathbb R ^ {m\times n} X={X(1,∗),X(2,∗),...,X(m,∗)}∈Rm×n,即有m个变量,每个变量有一个长度为n的序列。输出则是 A ∈ R m × m A\in\mathbb R^{m \times m} A∈Rm×m的非负有向矩阵。如果 A ( i , j ) A(i,j) A(i,j)远大于 0 0 0,那么说明第 i i i个变量是第 j j j个变量的影响因子之一。什么是非线性关系?论文中举了一个比较好的例子:
X ( 3 , t 3 ) = X ( 1 , t 1 ) 2 + l o g ( X ( 2 , t 1 ) ) + X ( 1 , t 2 ) X ( 3 , t 1 ) + X ( 1 , t 1 ) 3 c o s ( X ( 3 , t 2 ) ) X(3,t_3)=X(1,t_1)^2+log(X(2,t_1))+X(1,t_2)^{X(3,t_1)}+ X(1,t_1)^3cos(X(3,t_2)) X(3,t3)=X(1,t1)2+log(X(2,t1))+X(1,t2)X(3,t1)+X(1,t1)3cos(X(3,t2))
在上面这个式子中,变量 X 1 , X 2 , X 3 X_1, X_2, X_3 X1,X2,X3就不是简单的线性关系了,而是复杂的非线性关系。这种非线性是现有的任何方法都难以刻画的,那对这种复杂函数的拟合,咱们能想到什么?对,神经网络。所以在我看来,这篇论文的motivation还是挺好理解的。(吹吹牛皮,缓解一下枯燥)
现有的因果图学习的挑战主要集中在三个方面:
- 数据噪声对结果存在影响
- 系统具有多样性,很难有一个不需要领域知识的普适方法
- 结点数量增加带来的可扩展性问题(我理解为复杂度控制)
虽然提出了这么多挑战,但是他用神经网络的方法,这些问题都可以得到解决(至少是理论上的解决):
- 良好训练、鲁棒性高的神经网络具有较好的抗噪性
- 神经网络是数据驱动的,因此需要的领域知识较少;在论文中我们也可以看到,他应对不同数据集的方法就是增加可训练参数的数量&&把一些原本不可学习的参数变为可学习的。这个在后面会提到。
- 在神经网络中有一处要学一个 m × m m \times m m×m的矩阵,如果节点数增多,那么空间开销将不可承受,而考虑到节点之间的关系矩阵是低秩的(很难有一个节点被其他节点各种非线性组合决定之类的),所以可以做一个低秩分解,变成学习 m × k , k × k , k × m m \times k, k \times k, k \times m m×k,k×k,k×m这三个矩阵,然后重新组合成 m × m m \times m m×m的矩阵
相关方法
因为我的水平有限,所以这一段只能大致看一下增长见识,更多的内容要留待后续去阅读更多论文。这一段作者列举了如下的方法并和论文中提出的方法进行了对比:
-
Granger Causality
对于任意的两个变量,建立VAR模型并在有/无一个变量的情况下做F-test,然后比较并计算因果相关性。后续一些拓展的方法也大都依赖于VAR模型。这类方法有三个缺点:
- 它需要对任意的两个变量作F-test来计算因果性,这是基于数据集是正态分布的,而在实际应用中这并不一定成立
- 它只能计算两个变量之间的因果性,而不能计算多变量或者联合变量的因果性,因此有较高的虚报率
- VAR模型的固有属性依然是线性的,无法挖掘非线性关系
-
Transfer Entropy
在给定变量Y过往数据的情况下,如果变量X的过往数据可以显著降低Y未来数据包含的不确定性(由香农熵刻画),那么我们就说X是Y的一个影响因子。这种方法同样只能计算两个变量之间的因果性,所以和Granger Causality具有相似的局限性。
-
Graph Learning
通过在VAR模型中添加L1/2正则化项来学习因果性。按照我的理解,这种方法最后会得到一个与时间步相关的因果图。如果有 n n n个时间步,那么就有 n n n个因果图。对于任意的两个变量,如果这些因果图对应点的权值和接近于0,那么说明它们不具有因果性。这和这篇论文用的方法比较相似,但是并没有学到复杂的非线性关系,而只有多变量的线性因果性。
-
Kernel-based Methods
这类方法使用了基于核的VAR模型,从而可以提取一定的非线性关系。而这类方法主要的问题在于时间复杂度过高,比如这类方法中的某一个的复杂度是 O ( m 3 + n 3 ) O(m^3+n^3) O(m3+n3),因此只具备低可扩展性。
-
Supervised Learning Methods
这类方法将因果关联发掘问题转化为一个有监督的分类问题。给定任意两个变量的时序序列,分类器输出三种值的概率:1(X影响Y),-1(Y影响X),0(X、Y互不影响)。具体而言,模型将有无Y历史数据的X的条件分布通过核均值嵌入分别映射到重构核的希尔伯特空间中的两个点上,然后在这个空间里计算它们的距离,以此进行分类。这种方法需要标注的数据进行监督学习,在真实的应用场景中通常很难获得,因此具有较大的限制。
-
MLP and LSTM
与这篇论文除了网络结构之外几乎一致,可以说这篇论文能发就是因为它对于网络结构作了精细的调整,并对于每个地方都有较好的解释。
-
Graphical Neural Network
通过GNN而不是普通的MLP或者LSTM作多变量动态因果分析。论文相比这种方法的好处在于它专注于因果关系发掘的场景,而且低秩压缩的存在使得它具有较好的扩展性。
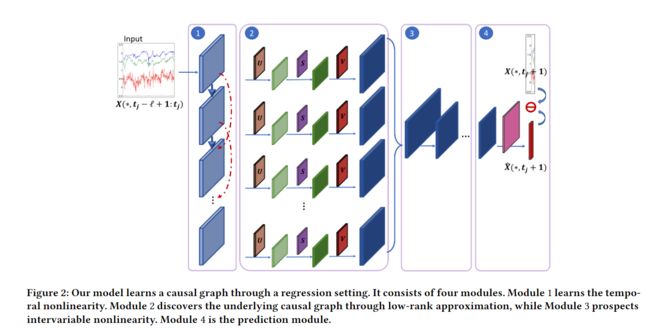
模型概述
模型分为四个部分,分别学习不同的非线性关系和因果关系。下面自底而上进行介绍(按照数据的流动方向):
模块 1:学习变量内非线性
论文使用神经网络的最大目的之一就是在因果学习中融入非线性。第一个模块只需要考虑单变量的非线性。在之前的例子中,前两项就是单变量的非线性,因为他们虽然是非线性的,但是每个项只和单个变量相关。论文中使用了ResNet作为变量非线性的刻画。公式如下:
G q = R e L U ( β q ( G q − 1 B q ) + i d ( G q − 1 ) ) , q = 1 , 2 , . . . , Q G 0 = X ( ∗ , t j − l + 1 , t j ) G_q=ReLU(\beta _q(G_{q-1}B_q)+id(G_{q-1})),\quad q=1,2,...,Q \\ G_0 = X(*, t_j-l+1,t_j) Gq=ReLU(βq(Gq−1Bq)+id(Gq−1)),q=1,2,...,QG0=X(∗,tj−l+1,tj)
其中:
- G q ∈ R m × p G_q\in \mathbb R^{m \times p} Gq∈Rm×p表示ResNet第q层的输出
- B q ∈ R p × p B_q\in \mathbb R^{p\times p} Bq∈Rp×p表示第q层的权值矩阵,第0层是 l × p l\times p l×p
- i d id id是恒等变换,这里不清楚第0层是如何处理的
- Q Q Q是ResNet层数
- β q \beta_q βq是每一层对最终结果的相关性,在对ResNet优化的后续论文中,一般是设置它为一个长度递减的固定值,但是在这篇论文中,由于对于不同的数据集每层都有不同的相关性,因此将这个变量设置为可学习的。下面是论文中为了论证这个可学习是合理的而提供的图

横轴是训练迭代数,纵轴是不同的层。可以看到,在两个不同的数据集上,最终参数都收敛了而且收敛到了不同的值。
由此我们得到了 Q Q Q个 m × p m\times p m×p的矩阵。这些矩阵代表了神经网络所拟合的只包含单个变量的非线性关系。它将作为下一层的输入。
模块 2:因果图学习(重点)
模块1中并没有考虑到不同变量对最终结果的贡献,模块2就是用来处理这个的。其实非常简单,直接乘上一个 A q A_q Aq矩阵就好,因为多变量更为复杂的非线性需要在模块3中处理。公式如下:
G ˉ q T ( ∗ , i ) = G q T A q ( ∗ , i ) , i = 1 , 2 , . . . , m \bar G_q^T(*,i)=G_q^TA_q(*,i),\quad i=1,2,...,m GˉqT(∗,i)=GqTAq(∗,i),i=1,2,...,m
这里的转置是为了让维度对齐。注意,如果这里直接这么处理,我们需要 q q q个 m × m m\times m m×m的可学习矩阵,在 m m m过大的时候这样的空间复杂度是无法承受的,所以我们需要降维。其实这个做法在深度学习中很常见,原本要学习一个 m × m m\times m m×m的矩阵,改为学习 m × k , k × k , k × m m\times k, k\times k, k\times m m×k,k×k,k×m的三个矩阵,只要结果正确即可。论文中说这样做的理论依据是虽然总体的 m m m可能很大,但是对每个变量有影响的平均节点数 k k k是比较小的。这是可以理解的,因为很难做到一个节点被其他很多很多节点影响。但是至于经过模块1的非线性层之后是不是这么回事,那就不清楚了。我这里还是保留意见。
那么这个就是论文在开头提到的 "low-rank decomposition" \text{"low-rank decomposition"} "low-rank decomposition",也是论文标题中的scalable。有了这样一个分解之后,我们就可以改写上式:
G ˉ q T ( ∗ , i ) = σ ( ( σ ( G q T U q , k ) S q , k ) V q , k ) \bar G_q^T(*,i)=\sigma ((\sigma (G_q^TU_{q,k})S_{q,k})V_{q,k}) GˉqT(∗,i)=σ((σ(GqTUq,k)Sq,k)Vq,k)
其中, U , S , V U,S,V U,S,V三个矩阵分别对应了前面提到的三个维度。在训练阶段结束后,令
A q ≈ U q , k S q , k V q , k A ≈ ∑ q = 1 Q β q A q A_q \approx U_{q,k}S_{q,k}V_{q,k} \\ A\approx \sum_{q=1}^Q\beta_qA_q Aq≈Uq,kSq,kVq,kA≈q=1∑QβqAq
则 A A A 就是对应该数据集的关联矩阵。
这里又存在一个问题了,为什么可以这样近似?理论上来说应该带上非线性层,但是带上非线性层会和数据相关,所以去掉了。那么这个贸然的去掉是否会给结果带来问题?会造成多大的精度损失?论文中并没有给出前人是否有相关的结论,只是说“Our empirical studies also confirm our choice.”。(我想这个地方大概就是它只能中B的原因?)论文中设置两个激活函数分别是tanh和ReLU(我特意去查了一下,tanh可以念作"tanch",哈哈哈)。
与传统的SVD分解相似,这里通过了正则化项让 U q , k , V q , k U_{q,k}, V_{q,k} Uq,k,Vq,k是标准正交的。这里提到了一句“The constructed embedding also has theoretical connection to Stiefel manifolds and spectral theorem[30].”,回头补一补相关文献。
Petre Stoica and Randolph L Moses. 1997.Introduction to spectral analysis. Vol. 1.Prentice hall Upper Saddle River, NJ.
模块 3:学习变量间非线性
通过前两个模块,我们得到了 Q Q Q个 m × p m\times p m×p的矩阵。我们将它们拼接在一起,输入到一个多层MLP中,最后得到一个 H D ∈ R m × d D H_D\in \mathbb R^{m\times d_D} HD∈Rm×dD的矩阵,其中 D D D是MLP的层数。然后论文对这个过程作了一些理论上的玄学解释,就略过去了。这里实在是有点过于简单了。
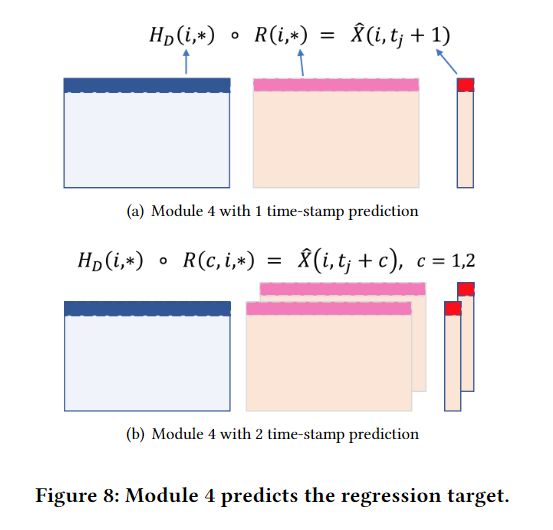
模块 4:回归预测
首先看传统的Granger Causality公式:
X ( ∗ , t j + 1 ) = ∑ r = 1 l A r X ( ∗ , t j + 1 − r ) + ϵ ( ∗ , t j + 1 ) X(*,t_j+1)=\sum_{r=1}^lA_rX(*,t_j+1-r)+\epsilon(*,t_j+1) X(∗,tj+1)=r=1∑lArX(∗,tj+1−r)+ϵ(∗,tj+1)
其中 A r A_r Ar是一个跟时间步相关的因果图矩阵。为了在神经网络中做回归,最后加了一个相同维度的矩阵去做行点积,运算结果作为预测结果:
X ^ ( i , t j + 1 ) = H D ( i , ∗ ) ∘ R ( i , ∗ ) , i = 1 , 2 , . . . , m \hat X(i, t_j+1)=H_D(i,*)\circ R(i,*), \quad i=1,2,...,m X^(i,tj+1)=HD(i,∗)∘R(i,∗),i=1,2,...,m
将预测结果和原结果做MSELoss,加上正则化项和标准正交的约束作为整体的loss:
l o s s = 1 m n ( X ( ∗ , t j + 1 ) − X ^ ( ∗ , t j + 1 ) ) 2 + λ 1 ∑ q ( ∣ ∣ U q , k ∣ ∣ 2 + ∣ ∣ V q , k ∣ ∣ 2 ) + λ 2 ∑ q ( ∣ ∣ U q , k T U q , k − I ∣ ∣ 2 + ∣ ∣ V q , k T V q , k − I ∣ ∣ 2 ) loss={1\over {mn}}(X(*, t_j+1)-\hat X(*, t_j+1))^2 \\ +\lambda_1\sum_q(||U_{q,k}||_2+||V_{q,k}||_2) \\ +\lambda_2\sum_q(||U_{q,k}^TU_{q,k}-I||_2+||V_{q,k}^TV_{q,k}-I||_2) loss=mn1(X(∗,tj+1)−X^(∗,tj+1))2+λ1q∑(∣∣Uq,k∣∣2+∣∣Vq,k∣∣2)+λ2q∑(∣∣Uq,kTUq,k−I∣∣2+∣∣Vq,kTVq,k−I∣∣2)
以上就是模型的整体框架,可以看到,重点就在于第二步的低秩分解。至于是否有效就需要在实验中进行验证。
实验部分
对比方法
和相关方法部分相对应,总共选取了5个baseline:
- VAR
最为有名的方法,通过自回归向量模型+L2正则化项来学习因果图 - PCKGC
源于成对的基于核的条件Granger因果性分析,只考虑了基于具有最高互信息分数的变量子集的条件概率,以此节省时间复杂度 - Copula
将每个变量的边缘分布转换到高斯域,然后使用VAR图学习方法+L2正则化项 - cLSTM
输入过往数据,经过LSTM后做未来数据的回归预测。使用L1正则化项并提取第一层的所有权重的绝对值和作为因果性的衡量 - pTE
先基于过往数据的概率函数将每个变量的时序信号转换成离散阶段,然后计算阶段的转化熵(也就是对应于之前的Transfer Entropy)的方法
数据集设置
数据集分为人造数据集和真实数据集。人造数据集采用了分层构造的方式,三层结构,上层是下层的影响因子,每层变量数按照5-15-45(A)和10-30-90(B)排列。

这样做主要是有利于观察结果,期望的因果图,有值的点应尽量集中在上部。

每个节点的时序序列通过一些复杂的非线性数学运算组合生成,并且加入一定的噪声。这里具体可以参考原论文。
实验结果
实验采用了PR曲线和ROC曲线对应围成的面积作为指标,结果如下:

对比其他方法在准确度上有了比较大的提升。为了证明他们的模型收敛情况良好,也给出了对应的loss曲线和AUPR曲线:

另外一部分是在真实数据集上做的,据论文作者描述,这些数据采集自50个引擎的历史六个月的数据,总共的训练样本数是180K。文章对最后的结果进行了一些描述,但是限制于隐私原因并没有描述的很清楚:
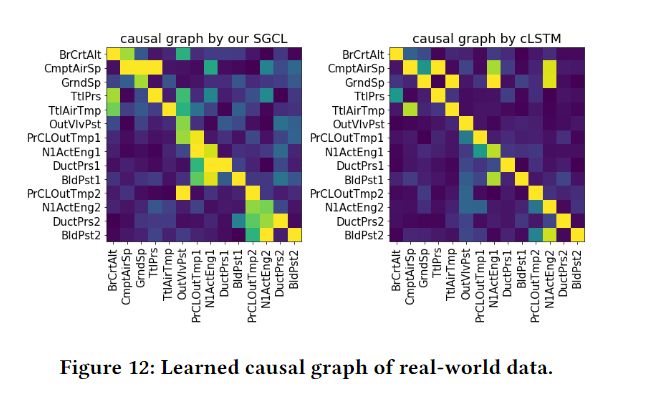
后面还有一些消融实验,不是重点,这里就略去了。唯一值得一提的是不同方法时间效率上的对比:

SCGL在m增大时的增长是这里面最缓慢的之一(cLSTM也很缓慢,但是结果上比不过SCGL)。
上面就是这篇论文的全部内容了,可能有些许遗漏。写这篇翻译的本意就是当一个备忘录,让自己看完论文之后还能留下点什么。从思路来看,他借鉴了相关方法里面的MLP&LSTM以及Granger Causality,设计了比较精细的网络结构,通过low-rank分解降低了时间复杂度,从而有所创新。但是看完整篇,我依然觉得在生成因果图的部分,他并没有说明为什么可以忽略掉非线性函数,只是用了约等号敷衍了过去。或许这是下一个可以突破的地方。后面我要做的事情,就是去了解相关方法中提到的那些前人工作,看看能不能得到相似的motivation。