Keras 中 L1正则化与L2正则化的代码用法和原理细致总结

本文属于知识点总结，内容属于摘抄和整理

一、概念介绍

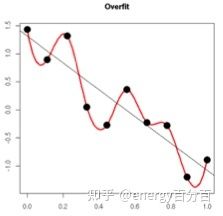
 我们先要理解什么是过拟合，以下图为例：

图中的红线为过拟合的曲线，而中间的黑线才是我们先要得到的拟合曲线，而得到为了黑线我们可以使用以下2种方法：

1. 减小拟合函数中的参数个数（简化拟合函数）
2. 限制拟合参数的弯曲程度

---

首先说一下L1正则化与L2正则化区别，其中常用的是L2正则化。两者的定义可以看下图：

 可以看出，之所以叫L2正则化，是因为它是平方项之和。所以从名字，就可以写出它们的表达式。

• L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
• L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合

附加知识：

稀疏模型与特征选择的关系

上面提到L1正则化有助于生成一个稀疏权值矩阵，进而可以用于特征选择。为什么要生成一个稀疏矩阵？

稀疏矩阵指的是很多元素为0，只有少数元素是非零值的矩阵，即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（term）作为一个特征，那么特征数量会达到上万个（bigram）。在预测或分类时，那么多特征显然难以选择，但是如果代入这些特征得到的模型是一个稀疏模型，表示只有少数特征对这个模型有贡献，绝大部分特征是没有贡献的，或者贡献微小（因为它们前面的系数是0或者是很小的值，即使去掉对模型也没有什么影响），此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。

L2正则化和过拟合的关系

拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是『抗扰动能力强』。

L0正则化与随机正则化

L0正则化使用L0范数来限制参数个数，从而避免模型过拟合；

随机正则化通过随机将某些函数参数置为0，从而简化网络结构，达到避免模型过拟合的目的，常用的方法有：

• 使用Relu或Gelu激活函数，将某些参数置为0
• 使用dropout网络结构，使某些神经单元失活，从而使某些参数为0

L1L2如何选择

L1正则化一般来说在需要进行特征选择的场景比较适用，如果不需要进行特征选择比如使用者就是想要把所有特征都考虑在内的话就用L2

二、Keras中的相关参数意义

在Keras中正则化有三种不同关键字参数，如下：

• kernel_regularizer：用于在网络层的权重上施加惩罚
• bias_regularizer：用于对网络层的偏置向量上施加惩罚
• activity_regularizer：用于对网络层的输出上施加惩罚

kernel_regularizer：初看似乎有点费解，kernel代表什么呢？其实在旧版本的Keras中，该参数叫做weight_regularizer，即是对该层中的权值进行正则化，亦即对权值进行限制，使其不至于过大。
bias_regularizer：与权值类似，限制该层中 biases 的大小。
activity_regularizer：更让人费解，activity又代表什么？其实就是对该层的输出进行正则化。

现在我们知道了这三个参数的异同，那么，我们该在什么时候使用哪一个参数呢？

1. 大多数情况下，使用kernel_regularizer就足够了；
2. 如果你希望输入和输出是接近的，你可以使用bias_regularizer；
3. 如果你希望该层的输出尽量小，你应该使用activity_regularizer。

三、在Keras代码中的用法

而在keras中正则化，有三种不同的策略，分别是：

L1正则化，L2正则化，L1_L2混合正则化。在代码中使用方式如下：

# 仅添加权重正则化
Dense(256, kernel_regularizer=keras.regularizers.l1(0.01))#加入l1
Dense(256, kernel_regularizer=keras.regularizers.l2(0.01))#加入l2
LSTM(256, kernel_regularizer=keras.regularizers.l1_l2(0.001, 0.01))#加入l1和l2
# 添加一些其他正则化
Dense(256, kernel_regularizer=keras.regularizers.l1(0.01),bias_regularizer=keras.regularizers.l1(0.01),activity_regularizer=keras.regularizers.l1(0.01))

这些L1正则化，L2正则化，L1_L2混合正则化，是什么原理，源码贴上来，可看可不看：

class L1L2(Regularizer):
    """Regularizer for L1 and L2 regularization.

    # Arguments
        l1: Float; L1 regularization factor.
        l2: Float; L2 regularization factor.
    """

    def __init__(self, l1=0., l2=0.):
        self.l1 = K.cast_to_floatx(l1)
        self.l2 = K.cast_to_floatx(l2)

    def __call__(self, x):
        regularization = 0.
        if self.l1:
            regularization += self.l1 * K.sum(K.abs(x))
        if self.l2:
            regularization += self.l2 * K.sum(K.square(x))
        return regularization

    def get_config(self):
        return {'l1': float(self.l1),
                'l2': float(self.l2)}
                
	def l1(l=0.01):
    	return L1L2(l1=l)


	def l2(l=0.01):
    	return L1L2(l2=l)


	def l1_l2(l1=0.01, l2=0.01):
    	return L1L2(l1=l1, l2=l2)






# 如何将其加入最终损失函数，拿Dense层为例：
#Dense层部分代码
def __init__(self, units,
                 activation=None,
                 use_bias=True,
                 kernel_initializer='glorot_uniform',
                 bias_initializer='zeros',
                 kernel_regularizer=None,
                 bias_regularizer=None,
                 activity_regularizer=None,
                 kernel_constraint=None,
                 bias_constraint=None,
                 **kwargs):
        self.kernel_regularizer = regularizers.get(kernel_regularizer)
        self.bias_regularizer = regularizers.get(bias_regularizer)
        self.activity_regularizer = regularizers.get(activity_regularizer)
def build(self, input_shape):
        assert len(input_shape) >= 2
        input_dim = input_shape[-1]

        self.kernel = self.add_weight(shape=(input_dim, self.units),
                                      initializer=self.kernel_initializer,
                                      name='kernel',
                                      regularizer=self.kernel_regularizer,
                                      constraint=self.kernel_constraint)





# 可以看到，正则化的添加，kernel,bias,activity是分开的。构建模型时，想用哪个，定义哪个。将正则化值添加进损失函数，主要表现在add_weight部分，keras层都继承自keras\engine\base_layer.py，其中有add_weight的定义
#add_weight完整代码
def add_weight(self,
                   name=None,
                   shape=None,
                   dtype=None,
                   initializer=None,
                   regularizer=None,
                   trainable=True,
                   constraint=None):
                   if shape is None:
            shape = ()
        initializer = initializers.get(initializer)
        if dtype is None:
            dtype = self.dtype
        weight = K.variable(initializer(shape, dtype=dtype),
                            dtype=dtype,
                            name=name,
                            constraint=constraint)
        if regularizer is not None: #此部分实现
            with K.name_scope('weight_regularizer'):
                self.add_loss(regularizer(weight))#利用add_loss函数加入
        if trainable:
            self._trainable_weights.append(weight)
        else:
            self._non_trainable_weights.append(weight)
        weight._tracked = True
        return weight

 四、数学原理

最后，解释一下为何L1正则化能产生稀疏矩阵。

假设只有一个参数为w，损失函数为L(w)，分别加上L1正则项和L2正则项后有：

假设L(w)在0处的倒数为d0，即

则可以推导使用L1正则和L2正则时的导数。
引入L2正则项，在0处的导数

 

 引入L1正则项，在0处的导数，因为有绝对值，所以求导是要考虑正负号。

 从上面的求导我们知道，在0处，导数可能不存在。
可见，引入L2正则时，代价函数在0处的导数仍是d0，无变化。

而L1正则化后，导数可能不存在。我们知道，取得极值的点，可能有两种，第一 是导数为0，第二是导数不存在。所以在w处可能取到极值。而我们优化的目标就是取到极值，所以，很大可能我们会来到w=0这个点。因此可能会存在很多w的值为0.
这里只解释了有一个参数的情况，如果有更多的参数，也是类似的。因此，用L1正则更容易产生稀疏解。
 

五、参考文献

最后附几篇参考文献：

1.这篇比较易懂

#透彻理解# 机器学习中，正则化如何防止过拟合 - 知乎 (zhihu.com)

机器学习中正则化项L1和L2的直观理解_小平子的专栏-CSDN博客_l2正则

2.这篇比较数学化，不建议看

正则化的通俗解释_正则化面经整理——from牛客_weixin_39633493的博客-CSDN博客 

深入理解L1、L2正则化 - 知乎 (zhihu.com)

3.这篇是实现的源码，做个记录

【TensorFlow】正则化方法tf.contrib.layers.l2_regularizer - 代码先锋网 (codeleading.com)

 Python regularizers.l2方法代码示例 - 纯净天空 (vimsky.com)

keras/regularizers.py at master · keras-team/keras (github.com)

4.局部涉及到L1/L2正则化的一些文章 

正则化 - 知乎 (zhihu.com)

 深度学习的正则化_最白の白菜的博客-CSDN博客

 正则化技术|深度学习中的正则化 (analyticsvidhya.com)

 TensorFlow2.0教程-Keras 快速入门 - 知乎 (zhihu.com)