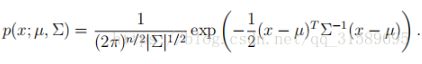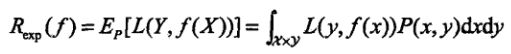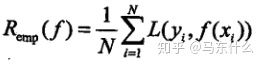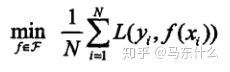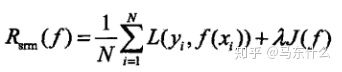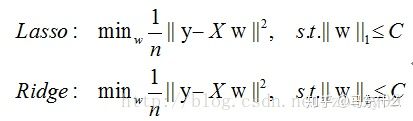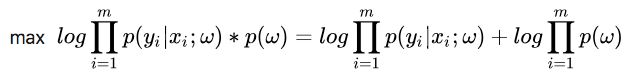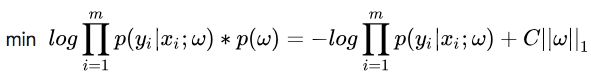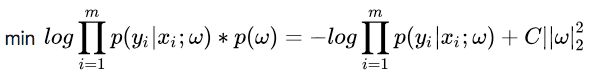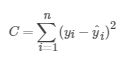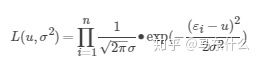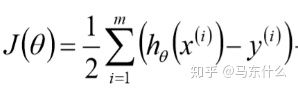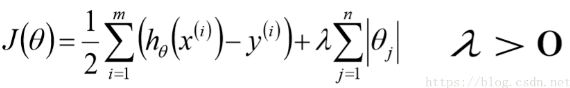正则化的通俗解释_正则化面经整理——from牛客
在解释正则化之前,老老实实的把李航的机器学习基础复习一遍,否则会很迷糊。网络上很多关于正则化的阐述都充满了偏见和个人主观理解,所以建议各位有书还是看经典的教材,毕竟写书的作者本身都是理论知识比较扎实的大牛,相对来说出错的可能性要低的多。博客推荐刘建平和苏剑林的都是业界比较有名的大佬,其它的csdn、博客园、知乎上的各种文章,谨慎阅读吧。
下面内容都是针对于有监督学习展开的。
在有监督学习中,将输入与输出所有可能取值的集合分别称为输入空间和输出空间,有时候把输入空间和特征空间等价,有时候认为特征空间是输入空间映射而成的(比如经过特征工程映射为特征空间然后入模)可以是有限元素也可以是整个欧式空间。https://blog.csdn.net/lulu950817/article/details/80424288 (帮助你理解一下欧式空间)
输入输出可以是同一个空间也可以是不同空间。有监督学习关于数据的基本假设就是输入数据X和输出数据y遵循某种联合概率分布P(X,y),训练数据和测试数据被看作是依联合概率分布P(X,y)独立同分布产生的。这是有监督学习的基本假设。
有监督学习的目的在于学习一个输入到输出的映射,这个映射就是通过模型来表示的,模型属于输入到输出空间的映射的集合,这个集合就是假设空间,由条件概率分布P(Y|X)或者决策函数Y=F(X)来表示,说人话就是假设我们认为输入和输出空间之间符合线性回归的线性映射关系则假设空间里的模型就包括了线性回归模型,最终得到的决策函数为y=Wt*X+b。
对于条件概率分布P(Y|X)比较典型直观的就是朴素贝叶斯模型了。
模型训练就是去求这么一个映射关系,使得经过映射输出的结果与真实的结果之间的误差尽可能小,并且对于未知数据也能有很好的推广。
对于有监督,无监督,强化学习等都遵从的三要素:
方法=模型+策略+算法
模型:含有所有可能的条件概率分布或决策函数,例如模型包含了lr、gbdt、svm、神经网络等等,假设空间的模型一般有无穷多个,可以定义为决策函数的函数族或者条件概率分布族:
其中,X和Y是定义在输入空间X和输出空间Y上的变量,这时F通常是一个由参数向量决定的函数族:
参数向量Theta取值于n维欧式空间Rn,称为参数空间。
假设空间也可以定义为条件概率的集合
相应的,F可以表示为一个参数向量决定的条件分布族:
决策函数称为非概率模型,条件概率模型称为概率模型。
策略:也就是按照什么样的准则学习或者选择最优的模型,我们的目的在于选择出最优模型,这里引入了损失函数与风险函数的概念。损失函数是用来度量模型一次映射结果的好坏;风险函数(期望损失)是用度量平均意义下模型预测的好坏。损失函数比较常见的有平方损失,对数损失等:
损失函数越小,模型就越好,因为我们的基本假设是输入和输出的X和Y服从一个未知的联合概率分布P(X,y),举例如下,多元正态分布:
上式为多元正态分布的数学式,其中x和u均为向量,x=【x1,x2,x3。。。。。。】
则x1,x2,x3。。。。。和y(这里就是指左边的那个p)之间是服从我们所说的”某种“概率分布的。
下面是损失函数的期望:
结合上面的多元正态分布的式子,损失函数的期望公式中P(X,y)对应的是上面的多元正态分布式子,而L(y,f(x))中的y为真实的标签值,f(x)为我们使用的模型所预测出的预测值,那么这个损失函数的期望的式子的含义也就很清楚了——就是损失函数L的期望啊哈哈哈哈哈哈哈,好像在说废话。严格来说应该是:
模型f(X)关于联合分布P(X,y)的平均意义下的损失,也称为风险函数或期望损失。
但是实际应用过程中我们一般也不知道P(X,y)是多少啊,如果知道了P(X,y),那么可以可以根据条件概率的公式直接计算出P(Y|X),(补充
条件概率=联合概率分布/对应的边缘概率分布,边缘概率通过联合概率分布公式分别对各个变量进行积分就可以得到了,具体的概率论与数理统计上有写。)
所以,一般来说我们的式子里面没法带P(X,y)联合概率分布项,(因为知道了这一项就不需要再用寻找什么模型来拟合了直接用上面的公式就可以得到一个条件概率模型的公式,使用这个公式直接就可以根据输入x计算出y值,这也是有监督学习的病态问题),所以退而求其次,我们引入了经验风险。
期望风险是模型关于联合分布的期望损失,经验风险则是模型关于这N个样本(也可以说是训练集)的平均损失,根据大数定律,当样本数量N趋于无穷大的时候,经验风险值趋于期望风险,所以一个很自然的想法是用经验风险估计期望风险(补充:这也解释了为什么海量的数据一阵乱怼很多时候要比少量数据精心做特征工程来的更好),但是实际过程中样本数量往往没有这么多,甚至很小,所以需要做一些别的事情来弥补一下样本数量的不足,这里又引入了:经验风险最小化和结构风险最小化。
经验风险最小化,顾名思义,按照经验风险最小化求出的模型就是最优模型:
其中F是假设空间(从调包侠的角度来说就是一大堆分类回归模型)。当样本数量足够大的时候,按照大数定律,这样产生的模型的效果会很不错,但是现实往往是样本容量不大甚至很小,那么拟合的效果就无法逼近期望风险了,从而产生了“过拟合”现象。
这个时候结构风险最小化上场,结构风险最小化等价于正则化,专门为防止过拟合而提出来的策略,就是经验风险最小化的式子+模型复杂度的正则化项或罚项(l1、l2正则,树模型的正则化等),定义如下;
其中J(f)是模型的复杂度,不同的算法可能有不同的定义模型复杂度的方式,这里是一个泛函式,白痴理解就是一个泛泛的函数,代表的是一个函数集,但是没有具体的公式就是了。累了剩下的一点内容截图吧。
算法:
一般来说很难找到全局最优解,但是很多时候局部最优解的效果已经很好了。
基础知识回顾完毕,进入正题。
什么是正则化?简述一下范数的意义是?
正则化就是结构风险最小化策略的实现,是在经验风险最小化的情况下加入一个正则化项或者罚项。范数是一种用来度量某个向量空间(或矩阵)中的每个向量的长度或大小的手段。
L1,L2正则化的原理和区别?为什么L1正则化会产生稀疏解而L2正则化会产生平滑解?
正则化是结构风险最小化策略的实现,L1和L2正则化属于正则化手段中的两种实现方式,L1正则化是在损失函数中加入 参数向量中各个元素的绝对值之和作为损失函数的惩罚项的,L2正则化是在损失函数中加入 参数向量中各个元素的平方,求和,然后再求平方根作为损失函数的惩罚项的。这就是二者的原理与区别。
问题二有多种角度的回答:
1、从几何角度:
(1)第一种,从目标函数与约束条件的图像上看:
摘自:https://www.cnblogs.com/demian/p/9436697.html
以lasso和ridge为例:
这里为了画图更加直观,我们将损失函数转换为有约束条件的最优化问题的形式。
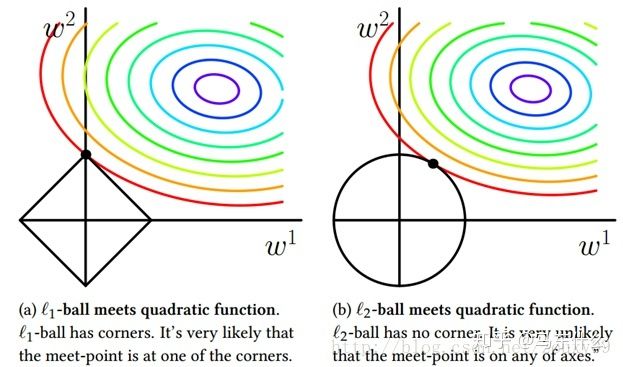
简单来说在多维空间中,l1正则化代表的约束条件是一个超立方体,它和每一个维度的坐标轴都会有一个“角”交点,目标函数大部分时候都会在“角”交点的地方相交,注意到在角的位置就会产生稀疏性,例如图中的相交点就有w1=0。
相对而言,l2正则化代表的约束条件在高维空间是一个超球体,因为没有角,所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了,倾向于得到均为非零的较小数,所以平滑。
总而言之即,L1正则化代表的约束条件的多维空间是超立方体和坐标轴存在很多“角”交点,目标函数大部分时候会在“角”的地方和约束条件相交,所以L1正则化容易产生稀疏的参数向量,而L2正则化是一个超球体,因为没有“角”交点,所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了,所以L2正则化容易产生平滑的参数向量。
(2)从两种正则化的参数求解速度上看
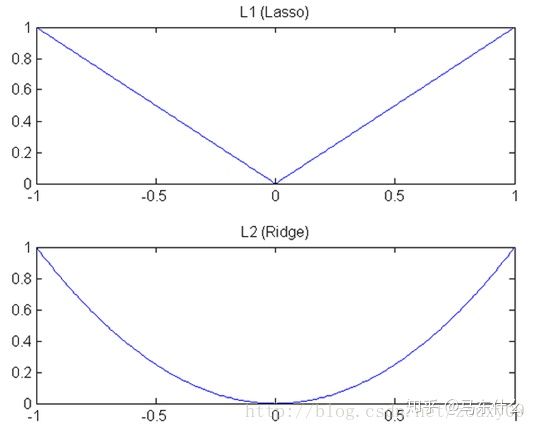
我们知道,L1和L2都是规则化的方式,我们将权值参数以L1或者L2的方式放到代价函数里面去。然后模型就会尝试去最小化这些权值参数。而这个最小化就像一个下坡的过程,L1和L2的差别就在于这个“坡”不同,如下图:L1就是按绝对值函数的“坡”下降的,而L2是按二次函数的“坡”下降。所以实际上在0附近根据其梯度,L1的下降速度比L2的下降速度要快。
2、贝叶斯统计学的角度(这个角度相对严谨一些)
L1则相当于设置一个Laplacean先验,去选择MAP(maximum a posteriori)假设。而L2则相当于Gaussian先验。也就是说这个时候无论是线性回归还是逻辑回归都不再是使用我们常见的极大似然法(MLE)来求解而是用贝叶斯估计的极大化后验概率(MAP)的方法来求解。
先假设参数 w 服从一种先验分布
,那么根据贝叶斯公式
求参数 w的时候,现在我们的极大似然函数就变成了:
式子(7),https://blog.csdn.net/hong__fang/article/details/78281200 证明过程(https://www.cnblogs.com/zjh225901/p/7495505.html 参考一下极大似然估计和贝叶斯估计原理的区别)在形式上就是极大似然估计的公式后面加了一个先验的概率密度函数项而已。
L1范数:
假设我们让 w 服从的分布为标准拉普拉斯分布,即概率密度函数为
,那么式子(7)多出的项就变成了 (ln之后参数项都用C代替简单方便的表示方式)
,其中C为常数了,重写式子:
取负数之后求最大值问题就变成求最小值问题所以这里变成minL2范数:
假设我们让w服从的分布为标准正态分布,即概率密度为
,那么式子(7)多出的项就成了 (ln之后参数项都用C代替简单方便的表示方式)
,其中C为常数,重写式子:
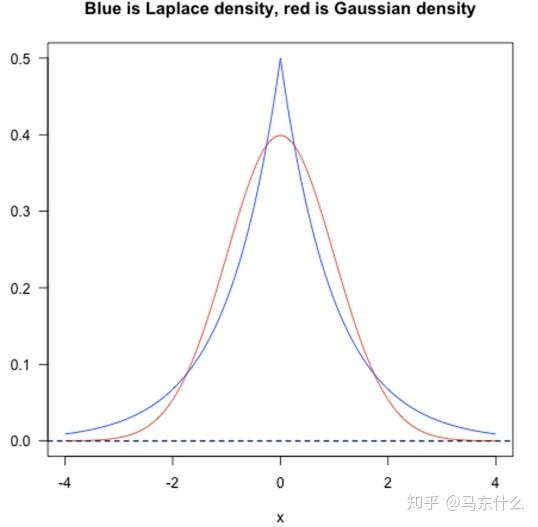
上图分别是标准拉普拉斯分布和标准正态分布的概率密度图像,可以看出,标准拉普拉斯分布在0位置的概率很高,标准正态分布在0附近的概率很高,因为正则项其实也是约束项,也就是说正则项的分布情况决定了最优解w的分布情况,所以说引入正则项之后其实是给权重w引入了先验分布。这个先验分布的分布情况决定了最终的最优解的分布情况。
https://blog.csdn.net/hong__fang/article/details/78281200 上述详细的推导过程
L1和L2除了正则化防止过拟合还有什么作用
防止过拟合的具体表现:在不显著增大偏差的的同时,显著减小模型的方差
L1正则化除了防止过拟合还可以作为特征筛选的方法,使得对模型不是太重要的特征的权重系数趋于0,那么我们就可以根据具体情况来对特征进行删除和重选择,从而起到提高泛化性能以及节约内存空间,提升运行效率的作用。
L1正则不是连续可导的,那么还能用梯度下降么,如果不能的话如何优化求解
L1正则相当于拉普拉斯先验,那么在损失函数为最小二乘法的时候,如何通过拉普拉斯先验推导出L1正则?
当使用最小二乘法的时候,我们的损失函数是均方误差,
我们在线性回归的面经整理的时候曾经遇到过一个问题就是为何线性回归使用均方误差作为损失函数:
https://blog.csdn.net/saltriver/article/details/57544704blog.csdn.net线性回归的基本假设之一,噪声服从正态分布,根据极大似然估计,我们的目的是在某个(u,σ2)(分别为噪声分布的均值和方差)下,使得服从正态分布的ε取得现有样本εi的概率最大。那么根据极大似然估计函数的定义可得:
继而一步一步推导到mse的损失函数的形式,具体推导步骤可见上面的blog,则:
这里贝叶斯方法通过最大化后验概率估计的公式作为l1和l2的一个公共的公式,只不过根据不同的正则化方法p(w)分别服从不同的先验分布,对这个式子取对数可以得到:
然后我们将拉普拉斯先验概率的公式带入上面式中的p(w),转换化简就可以得到l1正则化下的lasso的损失函数的形式了。只找到l2的证明截图,l1证明懒得写了,打公式挺累的,自己手推吧:
正则化与bias,variance的关系
从偏差-方差理论角度来说,正则化增大了偏差降低了方差;
L1和L2正则化各自优劣?以及适用场景?
我觉得说优劣是不是有点白痴了?不同的应用场景不同算法的特性不同怎么能这么直接的就说优劣呢?L1正则化一般来说在需要进行特征选择的场景比较适用,如果不需要进行特征选择比如使用者就是想要把所有特征都考虑在内的话就用l2呗
L1正则怎么处理0点不可导的情形?(这个谁会?近端梯度下降)
Lasso回归算法: 坐标轴下降法与最小角回归法小结www.cnblogs.coml2正则化所带来的惩罚项是可导的,所以ridge的求解不受什么限制,和普通的线性回归大同小异,一般来说常见的思路就是写出损失函数然后梯度下降即可。但是Lasso的损失函数是这样的:
惩罚项是l1范数,说白了就是套了个绝对值的符号,是不可导的,也就是说,我们的梯度下降法,牛顿法与拟牛顿法(上述方法都需要损失函数满足一阶可导)对它统统失效了。那我们怎么才能求有这个L1范数的损失函数极小值呢?
为什么L1、L2正则化为什么可以克服过拟合?
为了区分开l1、l2正则化和树的正则化,这里还是分开讨论,树的正则化放在gbdt的面经整理里。
角度1 偏差-方差理论:
说实话, 这个理论经常被人误用,知乎还是博客等等上面都有引述不准确的地方,首先,根据《机器学习》的定义,方差指的是同样大小的训练集变动所产生的数据扰动造成的影响,所以通过使用更多的数量或者是更少的特征来增大方差减少方差都是不准确的说法(虽然最终的结果看起来确实增大了偏差减少了方差)。
从偏差-方差理论的角度来说,在训练集大小不变而数据发生变动的情况下,正则化能够使得在偏差变化不显著的情况下,方差显著下降,也就是降低数据扰动造成的影响,从微观的层面来说,广义线性回归的权重系数会向0趋近(加入正则项后再去推导参数的更新公式可以得到这个趋于0的结论,具体可以参考lasso ridge的梯度更新公式,可参考https://blog.csdn.net/qq_40801709/article/details/85040684)即权重系数整体会变小,这就导致了当数据发生变动的时候,小系数相对于大系数,其预测结果的变动程度更小,从而达到降低方差的作用;
角度2 奥卡姆剃刀原则
在拟合能力接近的模型中,越简单的模型效果越好,有点扯,大概就类似于金融市场里面的“超跌必反弹”之类的“玄学”。
角度3 贝叶斯先验
前面我们证明过,加入l1、l2正则化就是引入权重系数w的先验分别为标准拉普拉斯先验概率分布和标准正态分布,引入了先验可以防止过拟合,比如:
投掷一枚均匀的硬币,如果投掷10次(训练集),则如果投掷10次都朝上则向上的概率为100%,明显结论不符合实际情况,如果加入了了0.5的先验概率,那么我们可以把先验概率和实际的概率进行一个加权组合比如 0.5*0.3+1*0.7=0.85,则错误的程度相对于训练集的100%的概率会有所下降从而更符合一般的情况。
再比如target encoding中也引入了先验概率的公式prior然后将训练集的计算概率和先验概率进行加权组合也是贝叶斯先验的一个反应。
、
正则化的本质是什么?
机器学习中L1正则化和L2正则化的区别是?
- 使用L1可以得到稀疏的权值
- 使用L1可以得到平滑的权值
- 使用L2可以得到稀疏的权值
- 使用L2可以得到平滑的权值
选AD
正则化L1,L2区别,适用于什么不同的场景
某些功能之间是否存在共线性?在这种情况下,L2正则化可以提高预测质量,正如其替代名称“岭回归”所暗示的那样。然而,一般来说,任何形式的正则化都将改善样本外的预测,无论是否存在多重共线性以及是否存在不相关的特征,仅仅因为正则化估计器的收缩特性。L1正则化无助于多重共线性; 它只会选择与结果具有最大相关性的特征。
L1正则化无助于多重共线性。L2正则化无法帮助进行特征选择
Ridge和Lasso的实现,他们的区别是什么?分别是如何求解的?
答:Ridge=线性回归+L2正则,有闭合解;Lasso=线性回归+L1正则,无闭合解,可用坐标梯度下降求解
lasso、ridge和线性回归的区别,为什么lasso能稀疏变量?
lasso和ridge分别是对线性回归进行l1和l2正则化约束之后进行训练得到的损失函数带约束项的线性回归方程。
linearregression的损失函数:
ridge的损失函数:
lasso的损失函数:
第三问上面写了不废话了。
在贝叶斯线性回归中:
假定似然概率和先验概率都为高斯分布, 假设先验概率的高斯准确率参数为a, 似然概率的高斯准确率参数为b, 则后验概率相当于平方误差+L2正则,则其正则化参数为
- a + b
- a / b
- a^2 + b^2
- a^2 / (b^2)
简单描述一下结构风险与经验风险?
from 统计学习方法
假设模型为f(x),输入为X,输出为y,X,y之间满足联合分布P(X,y),则期望风险为模型f(x)关于联合分布P(X,y)平均意义下的损失,公式如下:
但是因为一般P(X,y)是不知道的,因为如果联合分布知道的话可以通过联合分布和条件概率之间的公式直接转换得到P(Y|X)也就不需要模型去学习了,所以我们一般退而求其次,计算模型f(X)关于训练集D的平均意义下的损失即经验风险,公式如下:
其中N为样本数量,根据大数定律或PAC学习理论,N趋于无穷大时,经验风险趋于期望风险,但是因为现实中一般样本数量都是有限的,难以达到上述条件,所以需要对经验风险的公式进行矫正,衍生出两个有监督学习的基本策略:1、经验风险最小化ERM 2、结构风险最小化SRM。
当样本容量足够大时,经验风险最小化能保证有很好的学习效果,在现实中被广泛采用。比如,极大似然估计(maximum likelihood estimation)就是经验风险最小化的一个例子。当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化就等价于极大似然估计。公式定义如下:
但是,当样本容量很小时,经验风险最小化学习的效果就未必很好,会产生后面将要叙述的“过拟合(over-fitting)”现象。
结构风险最小化(structural risk minimization,SRM)是为了防止过拟合而提出来的
策略。结构风险最小化等价于正则化(regularization)。结构风险在经验风险上加上表示
模型复杂度的正则化项(regularizer)或罚项(penalty term)。在假设空间、损失函数以
及训练数据集确定的情况下,结构风险的定义是:
简单说,经验风险就是模型关于训练集的平均损失,结构风险是经验风险+正则损失项