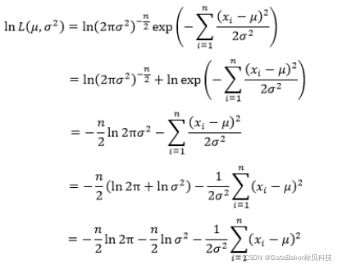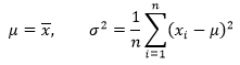GMM-HMM声学模型实例详解（标贝科技）

欢迎测试标贝科技AI开放平台 https://ai.data-baker.com/#/?source=qwer12

GMM-HMM声学模型实例详解

GMM-HMM为经典的声学模型，基于深度神经网络的语音识别技术，其实就是神经网络代替了GMM来对HMM的观察概率进行建模，建模解码等识别流程的格个模块仍然沿用经典的语音识别技术
接下来我将从GMM、最大似然估计到EM算法实例，再到最后使用一段语音介绍GMM-HMM声学模型参数更新过程

一、GMM (混合高斯分布)

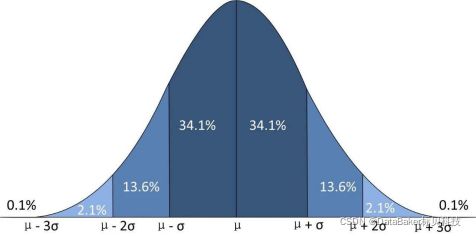
1、正态分布(高斯分布)
如果你绘制出来的概率分布是一条钟型曲线，且平均值、众数和中位数都是相等的，那么随机变量X就服从正态分布，记为X~N(μ，σ2),正态分布概率密度函数：
其中，μ是随机变量的均值，控制曲线的位置，σ^2控制曲线的陡峭程度

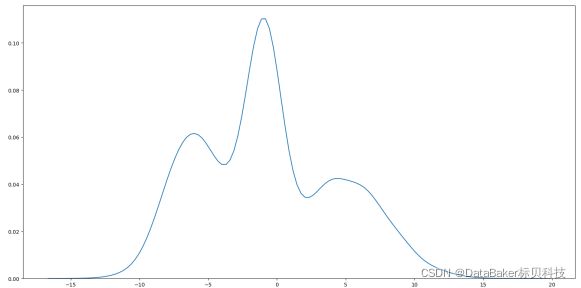
2、GMM (混合高斯分布)：
假设一批数据由三个不同的高斯分布生成，将这批数据混在一起，该分布就称为高斯混合分布，从数学上讲，认为这批数据的概率分布密度函数可以通过加权函数表示：

二、最大似然估计：

最大似然估计：使用概率模型，找到模型中的参数能够以较高概率产生观察数据；简单来说就是给定一组观察数据评估模型参数的方法。
比如：要统计全国成年人的身高分布情况，测量全部人口的身高耗费人力物力，假设身高服从正态分布，抽取1000人(抽取样本太少估计出的参数会不太准确)，根据这1000人的身高分布估计全国人口的身高分布情况，已知身高服从正态分布，n个人的最大似然函数表示为：

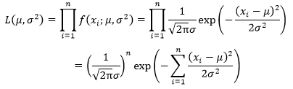
(1)直接求L的最大值可能不太好求，等式两边同时取对数，根据对数的性质可以将乘除法法转变为加减法

(2)整理化简公式

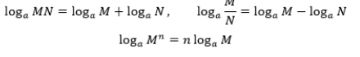
(3)对包含未知数的函数求最大值，可以分别对未知数(μ、σ^2)求导后令其等于0

(4)最终求得μ也就是样本的均值、σ^2也就是样本的方差:

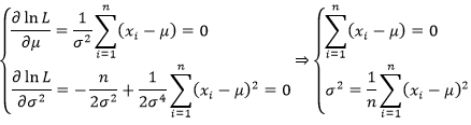
(5)根据1000人的身高信息分别求出μ、σ^2，
我们这里用10个人身高 做个示范,10个人身高分[150,155,180,165,170,156,170,183,160,185]
借用python代码计算:X~均值(μ=167.4)、方差(σ^2=137.24)、标准差(σ=11.71):

import numpy as np
student_height=np.array([150,155,180,165,170,156,170,183,160,185])
student_mean=np.mean(student_height)
print(student_mean)
print(np.var(student_height))
print(np.std(student_height))
>>167.4
>>137.24
>>11.71

(6)第五步中求出均值与方差，根据正态分布概率特点就可以计算出10W人(假设全国有10W人)的身高分布情况：
155.69——167.4(μ-σ~μ):=10000034.1%=34000人
167.4——179.11(μ~μ+σ):=10000034.1%=34000人
经计算可知，10W个人中身高在155.69~167.4有34000人；在167.4——179.11有34000人
三、EM算法估计

• 假设男女身高分别服从不同的正态分布，现在我想估计的更准确一些，用这10个人的身高[150,155,160,165,170,172,180,183,175,185]分别估计10W个人中男生、女生各自的身高分布情况
• 这10个人中我们不知道哪些是男生的身高，哪些是女生的身高，这时候可以借助EM算法进行估计

EM算法分为四个步骤：

(1) 给出观测值
(2) 利用对隐藏变量的现有估计值，计算其最大似然估计值
(3) 最大化(M)在E步上求得的最大似然值来更新参数的值
(4) 重复(2)-(3)直到收敛，停止迭代
在上面的例子中，隐含变量就是10个人男女身高情况，如果知道了10个人中具体的男女身高情况，就能计算出各自的身高分布情况，下面具体看下EM算法是如何进行估计的：

• 第一步，将10个人身高平均分配，假设前5个一个身高分布，后5个是一个身高分布
• 第二步，根据最大似然估计方法分别估计这两个身高正态分布的均值方差，借助python计算

x₁~(164.0,114)

import numpy as np
student_height=np.array([150,155,180,165,170])
student_mean=np.mean(student_height)
print(student_mean)
print(np.var(student_height))
print(np.std(student_height))
>>164.0
>>114.0
>>10.68

x₂~(170.8,137.36)

import numpy as np
student_height=np.array([156,170,183,160,185])
student_mean=np.mean(student_height)
print(student_mean)
print(np.var(student_height))
print(np.std(student_height))
>>170.8
>>137.36
>>11.72

• 第三步，根据这两个分布的参数，估计10个人身高分别属于哪个分布概率最大
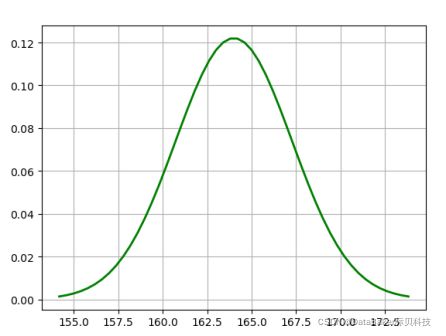
  绘制x₁~(164.0,114)的概率密度函数

import math
import numpy as np
import matplotlib.pyplot as plt
u = 164.0   # 均值μ
sig = math.sqrt(10.68)  # 标准差δ
x = np.linspace(u - 3*sig, u + 3*sig, 50)   # 定义域
y = np.exp(-(x - u) ** 2 / (2 * sig ** 2)) / (math.sqrt(2*math.pi)*sig) # 定义曲线函数
plt.plot(x, y, "g", linewidth=2)    # 加载曲线
plt.grid(True)  # 网格线
plt.show()  # 显示

绘制x₂~(170.8,137.36)的概率密度函数

import math
import numpy as np
import matplotlib.pyplot as plt
u = 170.8   # 均值μ
sig = math.sqrt(11.72)  # 标准差δ
x = np.linspace(u - 3*sig, u + 3*sig, 50)   # 定义域
y = np.exp(-(x - u) ** 2 / (2 * sig ** 2)) / (math.sqrt(2*math.pi)*sig) # 定义曲线函数
plt.plot(x, y, "g", linewidth=2)    # 加载曲线
plt.grid(True)  # 网格线
plt.show()  # 显示

由正态分布函数图可知，随机变量越靠近均值概率越大，如第一个身高值150,与第一个分布均值的距离为14(164-150),与第二个分布均值的距离为20.8(170.8-150)，故150属于第一个分布函数的概率更大，按此方法依次将10个数字分别归类
第一类分布：[150,155,165,156,160]
第二类分布：[180,170,170,183,185]

• 第四步

重复第二三步骤，直到第一类、第二类分布中数据不再变化，就完成了EM算法的整个过程；(由于第二步中不知道具体哪些属于男生身高哪些属于女生身高，所以采取平均分配的方式对其进行初始化；第三步中估计出均值与方差后对10个人的身高重新进行归类，此时有了一定的数学依据，所以比第一次分配更准确，以此类推获得最终的结果)

四、GMM-HMM声学模型参数更新

• 在声学模型中GMM主要的作用就是得到HMM中的发射概率(即GMM的均值和方差)，HMM的作用就是根据各个概率得到最优的音素，单词以及句子序列
• 总结来说HMM-GMM模型参数就是转移概率、混合高斯分布的均值、方差
• EM算法嵌入到整个GMM-HMM中完成模型参数的更新

1、如何将一段语音转换为想要表达的意思？
先介绍两个概念：

• 音素，汉语中一般使用声母与韵母作为音素集；
• 状态，可以理解为比音素更小的语音单位，习惯上把音素分为三个状态(初始、稳定、结束)

假设下面为一段5s的语音，语音内容为 : 下一个路口 (标注：x ia ii i g e l u k ou)，虽然已经给出这段语音的发音，但是对于哪些帧对应哪些音素(三个状态)的发音却是未知的，声学模型就是为了使声音信号对齐对应的音素(或音节)，在这个过程中使用GMM对帧与状态之间的关系进行建模，下面介绍具体的细节：

(1)第一：将这段语音以帧长10ms进行分帧，1s的语音被分为100帧，然后对每一帧提取mfcc特征(一般为39维)，这段语音就被表示成为(100,39)维的特征矩阵(截取前10帧)

（2） 第二：使用提取的mfcc特征训练GMM模型

1. 给出观测值
   训练开始时使用平均分配的方式初始化GMM模型(这里与上面EM中平均分配的意思一样)

• 以上面语音为例，语音被分为100帧，"x ia ii i g e l u k
  ou"为10个音素，平均分帧后每个音素为10帧，也就是"x"对应前10帧，"ia"对应10到20帧，依次分配：

• 每个音素又有三个状态,也就是1-4帧为状态①，5-7帧为状态②，8-10为状态③
  

2. 利用对隐藏变量的现有估计值，计算其最大似然估计值，这里的隐藏变量就是状态
   为了计算简单取mfcc的前两个维度保留两位小数进行说明：
   状态①(1~4帧):[(13.10,-43.36),(13.43,-40.74),(13.73,-41.76),(13.73,-42.08)]
   状态②(5~7帧):[(13.70,-41.16),(14.49,-25.57),(15.58,-16.46)
   状态③(8~10帧):(15.97,-12.37)],[(15.98,-6.50),(16.11,-0.63)
   状态①: 均值(13.497,-41.985) 方差(0.06766875,0.875075)
   状态②: 均值(14.59，-27.73) 方差(0.59406667，104.01446667)
   状态③: 均值(16.02,-6.5) 方差(4.06666667e-03,2.29712667e+01)

根据前面所说EM算法，计算欧式距离后可重新分配帧数所属状态,1_{5帧与均值(13.497,-41.985)距离更近，属于状态1,6}7帧属于状态2，8~10帧属于状态3(但在声学模型对齐过程中，还需要特征序列和标注文本（音素、状态）的对应关系，因此，需要对特征序列和标注文本对齐，所以实际训练过程中是将EM算法嵌入到GMM-HMM中，使用维特比或其他算法进行重新对齐)

• 如此就将输入特征(mfcc)与所有状态进行对应

然后通过统计的方式得到状态转移概率统计从状态①->①的转移次数，状态①->②的转移次数，除以总的转移次数，就可以得到每种转移的概率
3) 重新对齐(最大化(M)在E步上求得的最大似然值来更新参数的值)
根据2)得到的参数(转移概率、均值、方差)，重新对音频进行 【观察序列(特征)-状态序列】的对齐,2)初始化是通过均分进行了一次暴力对齐，3)的重新对齐是在2)得到的参数的基础上，使用算法对齐的。对齐方式有两种：采用viterbi算法的硬对齐，采用Baum-Welch学习算法（前向后向算法）的软对齐（这两个算法的实现细节，不在这里介绍了)
经过重新对齐后，每一帧对应的状态就会发生变化，GMM-HMM模型中的参数经重新计算后也会发生变化(对应EM算法中的M步)

4)重复2)-3)步多次，直至收敛，则该GMM-HMM模型训练完成。