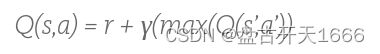白话解释DQN(DeepQ-Learning)强化学习算法(五子棋九宫格对弈实例)
介绍
本文公开一个基于dqn的九宫格游戏和五子棋游戏自动下棋算法源码,并对思路进行讲解。
源码地址:https://gitee.com/lizhigong/DQN-9pointgame
最近学习DQN算法绕了很多弯子,踩了很多坑,这里梳理一下,一来给自己学习过程留个记录,二来趁着坑比较热乎,写出来给大家分享分享。
代码中有居于ANN的九宫格游戏 已经训练好的
还有一个基于CNN的8*8的五子棋游戏 自己可以尝试着训练一下 自己试了试效果还不错
1、Q-Learning介绍
Q-Learning的思想并不是很复杂,很多文章都有详细的介绍,这里只是简单举个例子,不做详细讲解。
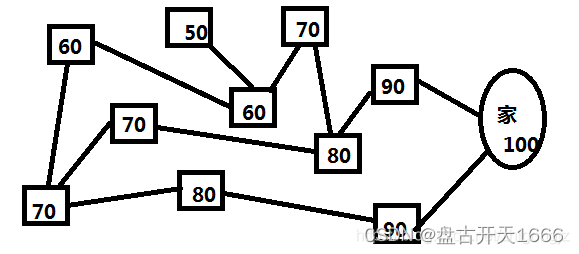
比如选择一条最近的路回家,而智能体可能出现在下面的方框中的任何一个位置,路线如下图所示。
那么怎么用Q-Learning解决路线选择的问题呢?
1、给所有的方框编上数字(价值数字)
2、选择下一个路线时,按照邻近的价值最高的方框选择,就能按照最近的路线回家。
那么问题来了:这上面的数字是我自己填的,那么机器学习的话这个数字怎么定?
1、初始化(全部的方框为0)
2、设定奖励值(到家得100分)
3、任意选择一个方框,开始走,每走一步,看看所在的方框邻近的连线里面,分值最高的数字是几,然后把这个数字乘以一个系数(图例中方框较少,所以固定减10,不至于出现0,如果方框较多的情况下,用减系数的方法会出现很多0的方框,这些0的方框就不好选择路线了,所以要用乘以一个系数),填到这个方框里面。然后反复的遍历,反复的走,直到最后,数字都固定下来了。
那么Q-leaning的公式自然就出来了
这里面每个方框表示一个状态,的Q(S,A)指的是目标方框的状态价值 ,也叫到目标位置的动作转移价值,这个比较绕,初学者可以直接理解为方框的价值(获取奖励的期望值、获取奖励的概率值等等,叫法很多,万变不离其宗,主要是理解里面的意思)。R指的是奖励值(到家得100分)那个阿拉伯R就是上面说的系数,如果没有这个系数,最后所有的方框都会变成100,还是没办法选路。max(Q)就是目标位置下一步所能达到的最大价值,也可以描述成目标位置下一步最大转移价值,我不知道我描述是否容易理解。
这个状态和状态之间的转移可以做成一个价值转移表。通过迭代完善表中的价值信息,这个过程就叫Q-leaning。
2、DQN介绍
DQN也叫deepQ-Learning,在Q-Learning前面加一个Deep。Q-Learning有一个缺点,如果状态特别多,比如五子棋的棋盘,每个位置都有(空白、黑子、白子)三个状态,那么假如一个10*10的棋盘 就有3^100个状态,那么这个Q表是没办法做出来的。那么我们就没办法构建这个Q表来获取状态价值状态转移价值了。
DQN就是搭建一个人工神经网络,输入是当前状态,输出是状态转移价值。或者输入是当前状态,输出是当前状态的Q值。通过多次迭代训练,使得神经网络输出逼近真实的Q值(逼近而不是等于,因为毕竟是神经网络,参数数量,存储占用量远小于Q表,如果能做到完全等于的话,还要存储干啥)
那么神经网络的训练的损失就是 预测Q值和(max(下一步的真实Q值)乘系数 +奖励值)的差的平方。 预测Q值就是神经网络一次前向传播输出的Q值,真实Q值就是神经网络曾经预测的Q值。为什么真实Q值是神经网络曾经预测过的Q值呢?因为神经网络每次训练都会对输出值产生影响,如果这个真实Q值一直变化的话,那么神经网络是没办法收敛的。所以需要搭建另一个参数一模一样的神经网络来生成真实Q值。这个生成真实Q值的网络不需要训练,只需要迭代一定次数以后,复制一份预测网络的参数即可。就好比一个笨老师教一个学生,学生学会了以后当了老师,教新的学生,然后青出于蓝而胜于蓝,这个学生越来越强。
本文中代码用的方法是,保存历史预测的Q值,等一个棋局结束后,再用这些Q值来训练每一步的预测Q值,这样做到一个神经网络就可以了。相当于一个聪明的学生,不停的复习,归纳,总结,然后逐渐变强。
3、对抗算法介绍
根据上面介绍的Q-Learning算法,解决的是一个单智能体的问题,这个智能体如何能够用最小的代价获得最大的回报。但是对弈的学习过程不一样,博弈中存在两个智能体,当前状态和当前动作对应的下一个状态会有很多,因为对手怎么下子我们不知道。那么当前状态和当前动作对应的什么状态是固定的呢?对手的状态。那么我能不能预测一下对手下一步能达到的最大的Q值呢?对手的Q值和我的Q值又有什么关系呢?对于零和博弈,对手的优势就是我得劣势,对手的劣势就是我的优势,那么我就可以用对手的Q值乘一个负的系数来训练当前的Q值。这样就解决了。
训练的过程就是,先自己和自己下一局棋,并记录每一步和每一步预测的最大Q值。等棋局结束后,再把整个棋局用神经网络"回顾"一遍,用记录的步子,Q值训练。
4、训练过程中注意的地方
下子的时候按照常理,咱们都是选择Q值最大的动作来下子,这样下子是没问题的,但是我们是来训练网络的,如果每次选择最大的步子下子的话容易陷入一个僵局。获胜方一直用同样或相似的套路打败败方,神经网络很快损失下降很快,但是还是不会正确的落子,或者说它只对某一种棋局局面的风格掌握得很好,对不按照套路出牌的人就没办法应对。那么我们就要加一个随即事件,一部分步子是按照最大值去走的,一部分步子是随机走的,但是最大Q值是每次都要计算出来保存用于回顾训练用的。这样很快就训练出一个会正确走子的九宫格游戏了。
不同的棋子最好放在不同的channel里面,我发现如果用0背景1白棋2黑棋这样标注放到一个棋盘里面神经网络无法收敛