【LeetBook】二叉树
参考资料:LeetBook / 二叉树
前言
差不多的解题思路就是dfs能够解决,其次就是bfs。
主要是递归的解法。
一刷就是了解了 解题的 思路
后序再补一些二叉树的题再刷一刷
目录
- 树的介绍
- 树的遍历
-
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历(广度优先搜索)
- 递归解决问题
-
- “自顶向下” 的解决方案
- “自底向上” 的解决方案
- 二叉树的最大深度
-
- “自顶向下”
- “自底向上”
- 对称二叉树
- 路径总和
- 构造二叉树
-
- 从中序与后序遍历序列构造二叉树
- 从前序与中序遍历序列构造二叉树
- 填充每个节点的下一个右侧节点指针
- 填充每个节点的下一个右侧节点指针 II
- 二叉树的序列化与反序列化
树的介绍
前序、中序、后序遍历,是取决于根节点的位置;
中序常用来在二叉搜索数中得到递增的有序序列;
后序可用于数学中的后缀表示法,结合栈处理表达式,每遇到一个操作符,就可以从栈中弹出栈顶的两个元素,计算并将结果返回到栈中;
代码表示一棵二叉树:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
树的遍历
前序遍历
输入:root = [1,null,2,3]
输出:[1,2,3]
public class TreeNodeTraversal {
/**
* 前序遍历
*
* @param root 二叉树
* @return java.util.List
*/
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
// preOrderRecursion(root, list);
preOrderIteration(root, list);
return list;
}
/**
* 前序遍历_递归
*
* @param tree 二叉树
* @param list 返回值
*/
public static void preOrderRecursion(TreeNode tree, List<Integer> list) {
if (tree == null) {
return;
}
list.add(tree.val);
// System.out.printf(tree.val + "\t");
preOrderRecursion(tree.left, list);
preOrderRecursion(tree.right, list);
}
/**
* 前序遍历_迭代
*
* @param tree 二叉树
* @param list 返回值
*/
public static void preOrderIteration(TreeNode tree, List<Integer> list) {
Deque<TreeNode> stack = new ArrayDeque<>();
// 压栈
stack.push(tree);
while (!stack.isEmpty()) {
// 出栈
TreeNode t1 = stack.pop();
// System.out.print(t1.val + "\t");
if (t1.right != null) {
stack.push(t1.right);
}
if (t1.left != null) {
stack.push(t1.left);
}
}
}
public static void main(String[] args) {
TreeNodeTraversal traversal = new TreeNodeTraversal();
TreeNode treeNode = new TreeNode(6,
new TreeNode(2, new TreeNode(1), new TreeNode(4, new TreeNode(3), new TreeNode(5))),
new TreeNode(7, null, new TreeNode(9, new TreeNode(8), null)));
traversal.preorderTraversal(treeNode);
}
}
中序遍历
输入:root = [1,null,2,3]
输出:[1,3,2]
public class TreeNodeTraversal {
/**
* 中序遍历
*
* @param root 二叉树
* @return java.util.List
*/
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
// inorderRecursion(root, list);
inorderIteration(root, list);
// [1, 2, 3, 4, 5, 6, 7, 8, 9]
return list;
}
/**
* 中序遍历_递归
*
* @param tree 二叉树
* @param list 返回值
*/
public static void inorderRecursion(TreeNode tree, List<Integer> list){
if (tree == null){
return;
}
inorderRecursion(tree.left, list);
list.add(tree.val);
// System.out.printf(tree.val + "\t");
inorderRecursion(tree.right, list);
}
/**
* 中序遍历_迭代
*
* @param tree 二叉树
* @param list 返回值
*/
public static void inorderIteration(TreeNode tree, List<Integer> list){
Deque<TreeNode> stack = new ArrayDeque<>();
while (tree != null || !stack.isEmpty()) {
while (tree != null) {
stack.push(tree);
tree = tree.left;
}
if (!stack.isEmpty()) {
tree = stack.pop();
// System.out.println(tree.val);
list.add(tree.val);
tree = tree.right;
}
}
}
public static void main(String[] args) {
TreeNodeTraversal traversal = new TreeNodeTraversal();
TreeNode treeNode = new TreeNode(6,
new TreeNode(2, new TreeNode(1), new TreeNode(4, new TreeNode(3), new TreeNode(5))),
new TreeNode(7, null, new TreeNode(9, new TreeNode(8), null)));
System.out.println(traversal.inorderTraversal(treeNode));
}
}
后序遍历
输入:root = [1,null,2,3]
输出:[3,2,1]
public class TreeNodeTraversal {
/**
* 后序遍历
*
* @param root 二叉树
* @return java.util.List
*/
public List<Integer> postorderTraversal(TreeNode root) {
ArrayList<Integer> list = new ArrayList<>();
// [1, 3, 5, 4, 2, 8, 9, 7, 6]
postorderIteration(root, list);
return list;
}
/**
* 后序遍历_递归
*
* @param tree 二叉树
* @param list 返回值
*/
public static void postorderRecursion(TreeNode tree, List<Integer> list){
if (tree == null){
return;
}
postorderRecursion(tree.left, list);
postorderRecursion(tree.right, list);
list.add(tree.val);
}
/**
* 后序遍历_迭代
*
* @param tree 二叉树
* @param list 返回值
*/
public static void postorderIteration(TreeNode tree, List<Integer> list){
if(tree == null){
return;
}
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode prePopNode = null;
while(stack.size() > 0 || tree != null){
if(tree != null){
// 遍历到左子树无路可走
stack.push(tree);
tree = tree.left;
} else {
// 能不能出栈,要判断,不同于中序遍历,可以直接出栈
TreeNode temp = stack.peek();
if(temp.right != null && temp.right != prePopNode){
// 右子树尚未遍历
tree = temp.right;
} else {
// 右子树为null或右子树已经遍历
prePopNode = stack.pop();
list.add(prePopNode.val);
tree = null;
}
}
}
}
public static void main(String[] args) {
TreeNodeTraversal traversal = new TreeNodeTraversal();
TreeNode treeNode = new TreeNode(6,
new TreeNode(2, new TreeNode(1), new TreeNode(4, new TreeNode(3), new TreeNode(5))),
new TreeNode(7, null, new TreeNode(9, new TreeNode(8), null)));
System.out.println(traversal.postorderTraversal(treeNode));
}
}
层序遍历(广度优先搜索)
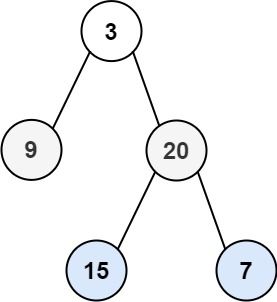
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
// 如果当前节点是空节点
if (root == null) {
// 直接返回空数组
return new ArrayList<>();
}
// 最终返回值
List<List<Integer>> res = new ArrayList<>();
// 栈
Deque<TreeNode> stack = new ArrayDeque<>();
// 当前栈压入元素
stack.offer(root);
// 当前栈里面有元素
while (stack.size() != 0) {
// 当前栈的长度
int levelNum = stack.size();
// 每层遍历的列表:存储的是每层的结点值
List<Integer> temp = new ArrayList<>();
// 限制每次取元素的次数
for (int i = 0; i < levelNum; i++) {
//出队
TreeNode cur = stack.poll();
// 存储每层的结点值
temp.add(cur.val);
// 弹出节点是否存在左子树
if (cur.left != null) {
// 往栈末尾存入弹出节点的左子树
stack.offer(cur.left);
}
// 弹出节点是否存在右子树
if (cur.right != null) {
// 往栈末尾存入弹出节点的右子树
stack.offer(cur.right);
}
}
//把每层的结点值存储在res中,
res.add(temp);
}
// 返回
return res;
}
public static void main(String[] args) {
Solution solution = new Solution();
TreeNode treeNode = new TreeNode(6,
new TreeNode(2, new TreeNode(1), new TreeNode(4, new TreeNode(3), new TreeNode(5))),
new TreeNode(7, null, new TreeNode(9, new TreeNode(8), null)));
List<List<Integer>> lists = solution.levelOrder(treeNode);
System.out.println(lists);
}
}
递归解决问题
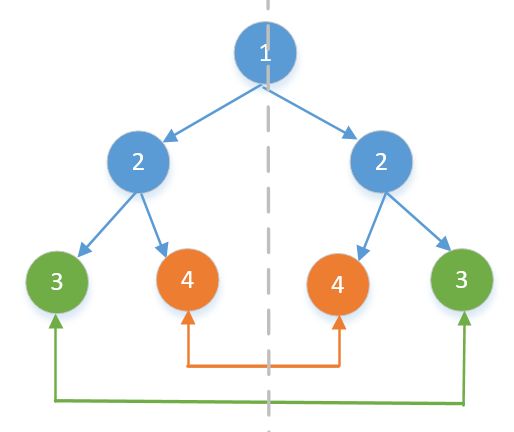
“自顶向下” 的解决方案
其实就是前面提到的前序遍历。
private int answer; // don't forget to initialize answer before call maximum_depth
private void maximum_depth(TreeNode root, int depth) {
if (root == null) {
return;
}
if (root.left == null && root.right == null) {
answer = Math.max(answer, depth);
}
maximum_depth(root.left, depth + 1);
maximum_depth(root.right, depth + 1);
}
“自底向上” 的解决方案
后序遍历。上层数值依赖于下层数值,最后得到两个值(根的左子树的深度和根的右子树的深度)取最大值即可
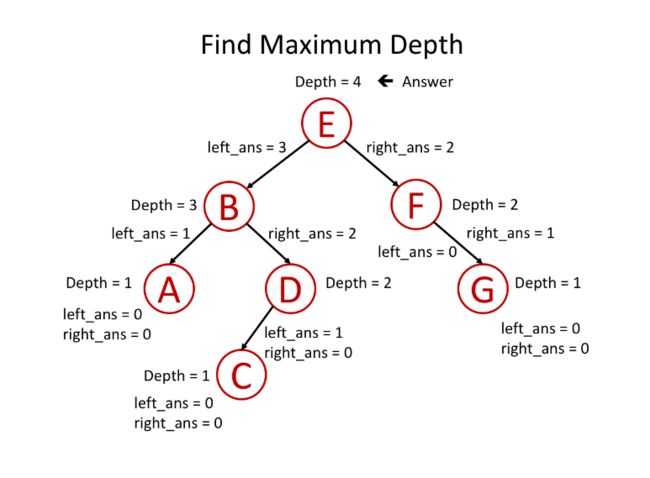
public int maximum_depth(TreeNode root) {
if (root == null) {
return 0; // return 0 for null node
}
int left_depth = maximum_depth(root.left);
int right_depth = maximum_depth(root.right);
return Math.max(left_depth, right_depth) + 1; // return depth of the subtree rooted at root
}
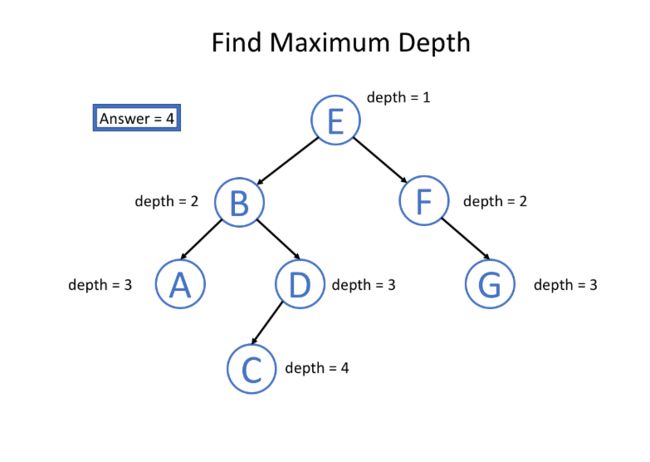
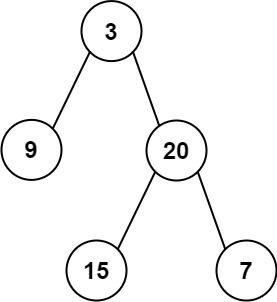
二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],返回它的最大深度 3
3
/ \
9 20
/ \
15 7
“自顶向下”
class Solution {
private int answer;
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
dfs(root, 1);
return answer;
}
private void dfs(TreeNode root, int depth) {
if (root == null) {
return;
}
if (root.left == null && root.right == null) {
answer = Math.max(answer, depth);
}
dfs(root.left, depth + 1);
dfs(root.right, depth + 1);
}
public static void main(String[] args) {
Solution solution = new Solution();
TreeNode treeNode = new TreeNode(6,
new TreeNode(2, new TreeNode(1), new TreeNode(4, new TreeNode(3), new TreeNode(5))),
new TreeNode(7, null, new TreeNode(9, new TreeNode(8), null)));
System.out.println(solution.maxDepth(treeNode));
}
}
“自底向上”
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftLength = maxDepth(root.left);
int rightLength = maxDepth(root.right);
return Math.max(leftLength, rightLength) + 1;
}
public static void main(String[] args) {
Solution solution = new Solution();
TreeNode treeNode = new TreeNode(6,
new TreeNode(2, new TreeNode(1), new TreeNode(4, new TreeNode(3), new TreeNode(5))),
new TreeNode(7, null, new TreeNode(9, new TreeNode(8), null)));
System.out.println(solution.maxDepth(treeNode));
}
}
对称二叉树
class Solution {
public boolean isSymmetric(TreeNode root) {
return isMirror(root, root);
}
public boolean isMirror(TreeNode left, TreeNode right) {
// 如果左右子节点都为空,说明当前节点是叶子节点,返回true
if (left == null && right == null) return true;
// 如果当前节点只有一个子节点或者有两个子节点,但两个子节点的值不相同,直接返回false
if (left == null || right == null || left.val != right.val) return false;
// 左子节点的左子节点和右子节点的右子节点比较
boolean leftBoolean = isMirror(left.left, right.right);
// 左子节点的右子节点和右子节点的左子节点比较
boolean rightBoolean = isMirror(left.right, right.left);
return leftBoolean && rightBoolean;
}
public static void main(String[] args) {
Solution solution = new Solution();
TreeNode treeNode = new TreeNode(1,
new TreeNode(2, new TreeNode(3), new TreeNode(4)),
new TreeNode(2, new TreeNode(4), new TreeNode(3)));
System.out.println(solution.isSymmetric(treeNode));
}
}
路径总和
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
我这里是用每条路径相加去判断的。
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null){
return false;
}
int cur = 0;
return dfs(root, cur, targetSum);
}
private boolean dfs(TreeNode root, int cur, int targetSum) {
if (root == null) {
return false;
}
// 当前层数的路径
cur = cur + root.val;
// root.left == null && root.right == null 确保到达叶子节点
// cur == targetSum 根节点到叶子节点的路径是否等于目标值
if (root.left == null && root.right == null && cur == targetSum) {
return true;
}
return dfs(root.left, cur, targetSum) || dfs(root.right, cur, targetSum);
}
public static void main(String[] args) {
Solution solution = new Solution();
TreeNode treeNode = new TreeNode(6,
new TreeNode(2, new TreeNode(1), new TreeNode(4, new TreeNode(3), new TreeNode(5))),
new TreeNode(7, null, new TreeNode(9, new TreeNode(8), null)));
System.out.println(solution.hasPathSum(treeNode, 31));
}
}
其实,可以通过相减去判断
public boolean hasPathSum(TreeNode root, int sum) {
//如果根节点为空,或者叶子节点也遍历完了也没找到这样的结果,就返回false
if (root == null)
return false;
//如果到叶子节点了,并且剩余值等于叶子节点的值,说明找到了这样的结果,直接返回true
if (root.left == null && root.right == null && sum - root.val == 0)
return true;
//分别沿着左右子节点走下去,然后顺便把当前节点的值减掉,左右子节点只要有一个返回true,
//说明存在这样的结果
return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}
构造二叉树
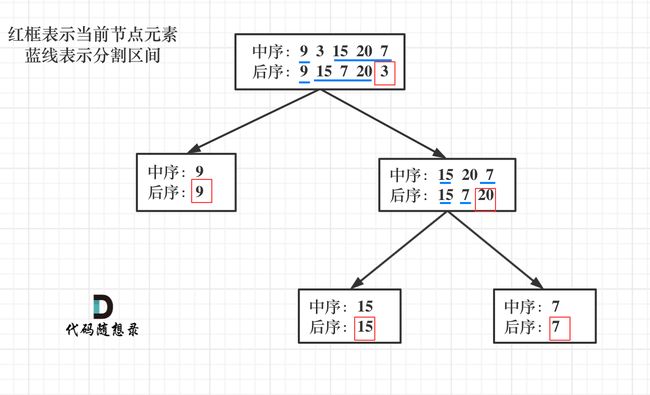
从中序与后序遍历序列构造二叉树
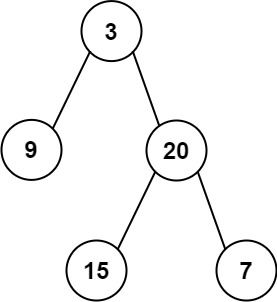
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
int len = inorder.length;
if (len == 0) {
return null;
}
return dfs(inorder, postorder, 0, len - 1, 0, len - 1);
}
/**
* 组成二叉树
*
* @param inorder 原始中序
* @param postorder 原始后序
* @param inorderHead 中序头下标
* @param inorderTail1 中序尾下标
* @param postorderHead 后序头下标
* @param postorderTail 后序尾下标
* @return TreeNode
*/
TreeNode dfs(int[] inorder, int[] postorder, int inorderHead, int inorderTail1, int postorderHead, int postorderTail) {
if (postorderHead > postorderTail) {
return null;
}
// 根节点的值
int val = postorder[postorderTail];
// 创建根节点
TreeNode root = new TreeNode(val);
// 后序头下标 和 尾下标 对应的数组 只有一个元素了
if (postorderHead == postorderTail) {
return root;
}
//拆分点mid的位置是相对的,因为 inorderHead != postorderHead
int mid = 0;
// 找到分割位置
while (inorder[inorderHead + mid] != val) {
mid++;
}
root.left = dfs(inorder, postorder, inorderHead, inorderHead + mid - 1, postorderHead, postorderHead + mid - 1);
root.right = dfs(inorder, postorder, inorderHead + mid + 1, inorderTail1, postorderHead + mid, postorderTail - 1);
return root;
}
public static void main(String[] args) {
Solution solution = new Solution();
TreeNode treeNode = solution.buildTree(new int[]{9, 3, 15, 20, 7}, new int[]{9, 15, 7, 20, 3});
System.out.println(treeNode);
}
}
从前序与中序遍历序列构造二叉树
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
跟前面的解法类似:
比如说:

不断地通过前序的第一个值,来确定中序当前值的左区间以及右区间。
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
int length = preorder.length;
if (length < 1) {
return new TreeNode();
}
return dfs(preorder, inorder, 0, length - 1, 0, length - 1);
}
/**
* 根据中序和前序遍历组成二叉树
*
* @param preorder 原始前序遍历
* @param inorder 原始中序遍历
* @param preorderHead 前序头下标
* @param preorderTail 前序尾下标
* @param inorderHead 中序头下标
* @param inorderTail 中序尾下标
* @return TreeNode
*/
TreeNode dfs(int[] preorder, int[] inorder, int preorderHead, int preorderTail, int inorderHead, int inorderTail) {
if (inorderHead > inorderTail) {
return null;
}
// 前序遍历确定节点的值
int value = preorder[preorderHead];
// 创建一个节点
TreeNode root = new TreeNode(value);
// 当前中序的区间只剩下一个元素,则直接返回即可
if (inorderHead == inorderTail) {
return root;
}
// 找出中序的中间下标
// 用于分割左子树和右子树
int mid = 0;
while (inorder[inorderHead + mid] != value) {
mid++;
}
root.left = dfs(preorder, inorder, preorderHead + 1, preorderHead+ mid, inorderHead, inorderHead + mid - 1);
root.right = dfs(preorder, inorder, preorderHead + mid + 1, preorderTail, inorderHead + mid + 1, inorderTail);
return root;
}
public static void main(String[] args) {
Solution solution = new Solution();
TreeNode treeNode = solution.buildTree(new int[]{1, 2, 3}, new int[]{3, 2, 1});
System.out.println(treeNode);
}
}
填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
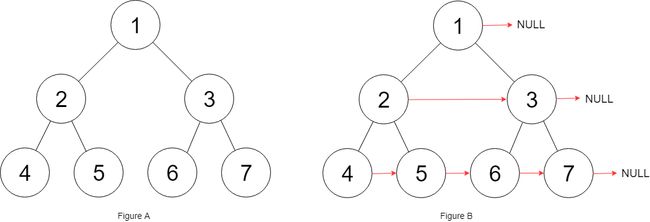
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
class Solution {
public Node connect(Node root) {
if (root != null) {
dfs(root.left, root.right);
}
return root;
}
void dfs(Node left, Node right) {
if (left == null || left.next == right) {
return;
}
left.next = right;
dfs(left.left, left.right);
dfs(left.right, right.left);
dfs(right.left, right.right);
}
public static void main(String[] args) {
Solution solution = new Solution();
Node treeNode = new Node(
1,
new Node(2,
new Node(4),
new Node(5),
null
),
new Node(3,
new Node(6),
new Node(7),
null
),
null
);
Node connect = solution.connect(treeNode);
System.out.println(connect);
}
}
填充每个节点的下一个右侧节点指针 II
class Solution {
public Node connect(Node root) {
if (root == null) {
return null;
}
if (root.left != null) {
if (root.right != null) {
root.left.next = root.right;
} else {
root.left.next = connectHelper(root.next);
}
}
if (root.right != null) {
root.right.next = connectHelper(root.next);
}
connect(root.right);
connect(root.left);
return root;
}
public Node connectHelper(Node root) {
if (root == null) {
return null;
}
if (root.left != null) {
return root.left;
}
if (root.right != null) {
return root.right;
}
return connectHelper(root.next);
}
public static void main(String[] args) {
Solution solution = new Solution();
Node treeNode = new Node(
1,
new Node(2,
new Node(4),
new Node(5),
null
),
new Node(3,
null,
new Node(7),
null
),
null
);
Node connect = solution.connect(treeNode);
System.out.println(connect);
}
}
二叉树的序列化与反序列化
public class Codec
{
//把树转化为字符串(使用DFS遍历,也是前序遍历,顺序是:根节点→左子树→右子树)
public String serialize(TreeNode root) {
//边界判断,如果为空就返回一个字符串"#"
if (root == null) {
return "#";
}
return root.val + "," + serialize(root.left) + "," + serialize(root.right);
}
//把字符串还原为二叉树
public TreeNode deserialize(String data) {
String[] split = data.split(",");
//把字符串data以逗号","拆分,拆分之后存储到队列中
Queue<String> queue = new LinkedList<>(Arrays.asList(split));
return helper(queue);
}
private TreeNode helper(Queue<String> queue) {
//出队
String sVal = queue.poll();
//如果是"#"表示空节点
if ("#".equals(sVal)) {
return null;
}
//否则创建当前节点
TreeNode root = new TreeNode(Integer.valueOf(sVal));
//分别创建左子树和右子树
root.left = helper(queue);
root.right = helper(queue);
return root;
}
public static void main(String[] args) {
Codec solution = new Codec();
TreeNode treeNode = new TreeNode(3,
new TreeNode(5,
new TreeNode(6),
new TreeNode(2,
new TreeNode(7),
new TreeNode(4))),
new TreeNode(1,
new TreeNode(0),
new TreeNode(8)));
String connect = solution.serialize(treeNode);
System.out.println(connect);
TreeNode deserialize = solution.deserialize(connect);
System.out.println(deserialize.toString());
}
}