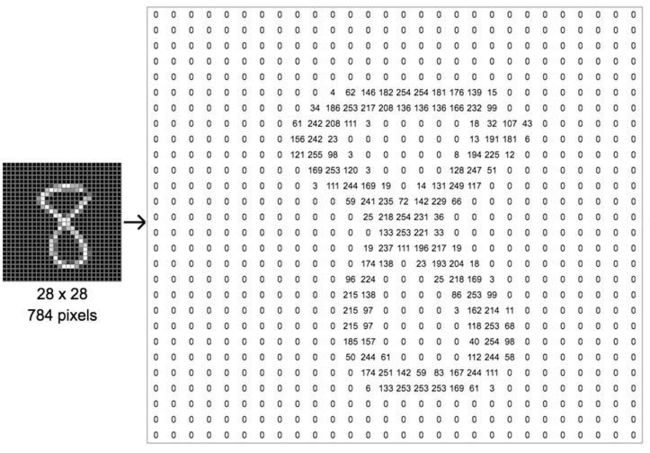
- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
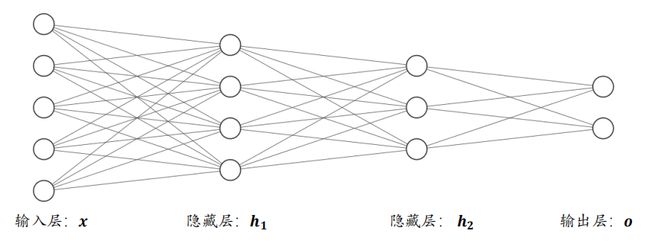
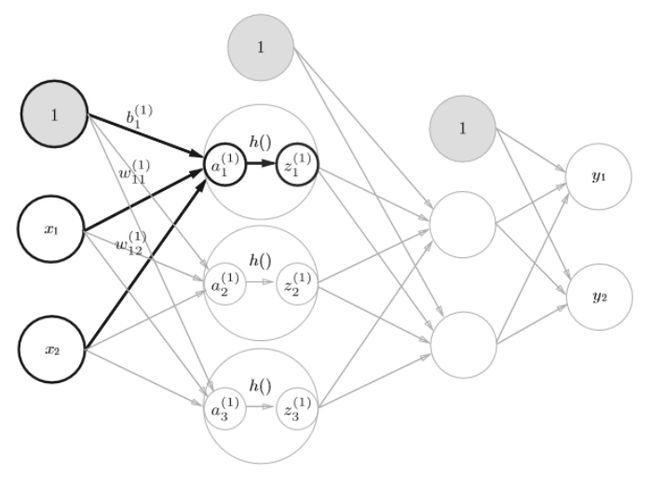
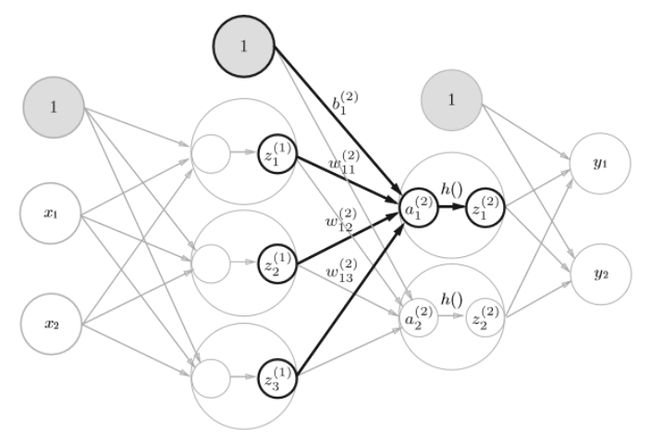
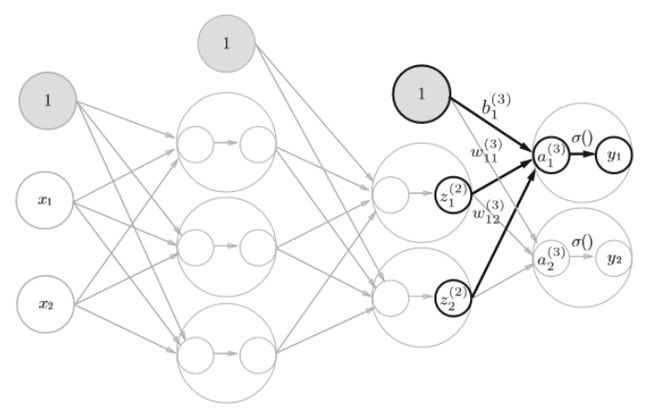
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- 将cmd中命令输出保存为txt文本文件
落难Coder
Windowscmdwindow
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码,无可厚非,我们有必要保存我们的炼丹结果,但是复制命令行输出到txt是非常麻烦的,其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是:运行指令>输出到的文件名称或者具体保存路径测试下,我打开cmd并且ping一下百度:pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出:如果你再
- 番茄西红柿叶子病害分类数据集12882张11类别
futureflsl
数据集分类数据挖掘人工智能
数据集类型:图像分类用,不可用于目标检测无标注文件数据集格式:仅仅包含jpg图片,每个类别文件夹下面存放着对应图片图片数量(jpg文件个数):12882分类类别数:11类别名称:["Bacterial_Spot_Bacteria","Early_Blight_Fungus","Healthy","Late_Blight_Water_Mold","Leaf_Mold_Fungus","Powdery
- Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
- xilinx vivado PULLMODE 设置思路
坚持每天写程序
fpga开发
1.xilinx引脚分类XilinxIO的分类:以XC7A100TFGG484为例,其引脚分类如下:1.UserIO(用户IO):用户使用的普通IO1.1专用(Dedicated)IO:命名为IO_LXXY_#、IO_XX_#的引脚,有固定的特定用途,多为底层特定功能的直接实现,如差分对信号、关键控制信号等,不能随意变更。1.2多功能(Multi-Function)IO:命名为IO_LXXY_ZZ
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- K近邻算法_分类鸢尾花数据集
_feivirus_
算法机器学习和数学分类机器学习K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
- 网络通信流程
记得开心一点啊
服务器网络运维
目录♫IP地址♫子网掩码♫MAC地址♫相关设备♫ARP寻址♫网络通信流程♫IP地址我们已经知道IP地址由网络号+主机号组成,根据IP地址的不同可以有5钟划分网络号和主机号的方案:其中,各类地址的表示范围是:分类范围适用网络网络数量主机最大连接数A类0.0.0.0~127.255.255.255大型网络12616777214【(2^24)-2】B类128.0.0.0~191.255.255.255中
- 5分钟说透AppStore审核原理,让你拥有上架新思路!
Q仔本人噢
在AppStore上架是越来越难了!相信非常多公司的技术人员都为此困扰,然而外包团队水平又层次不齐,容易遇坑,实在是内忧外患。是什么原因导致审核机制频繁调整?又是什么原因使得审核变得越发严格?那么接下来听小Q分解,马上给各位带来解答!首先看一下近一年的上下架的情况:近一年上架情况近一年下架情况通过数据我们发现越是马甲包产量权重高的分类里被下架的app数量越多,苹果此举可谓是上有政策,下有对策。通过
- 遥感影像的切片处理
sand&wich
计算机视觉python图像处理
在遥感影像分析中,经常需要将大尺寸的影像切分成小片段,以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务,如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程,同时确保每个影像片段保留正确的地理信息。准备环境首先,确保安装了必要的Python库,包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
- 《转介绍方法论》学习笔记
小可乐的妈妈
一、高效转介绍的流程:价值观---执行----方案一)转介绍发生的背景:1、对象:谁向谁转介绍?全员营销,人人参与。①员工的激励政策、客户的转介绍诱因制作客户画像:a信任;支付能力;意愿度;便利度(根据家长具备四个特征的个数分为四类)B性格分类C职业分类D年龄性别②执行:套路,策略,方法,流程2、诱因:为什么要转介绍?认同信任;多方共赢;传递美好;零风险承诺打动人心,超越期待。选择做教育,就是选择
- JAVA学习笔记之23种设计模式学习
victorfreedom
Java技术设计模式androidjava常用设计模式
博主最近买了《设计模式》这本书来学习,无奈这本书是以C++语言为基础进行说明,整个学习流程下来效率不是很高,虽然有的设计模式通俗易懂,但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番,发现有大神写过了这方面的问题,于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类:创建型模式,共五种:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式,共七种:适配器
- 100天持续行动—Day01
Richard_DL
今天开始站着学习,发现效率大幅提升。把fast.ai的Lesson1的后半部分和Lesson2看完了。由于Keras版本和视频中的不一致,运行notebook时经常出现莫名其妙的错误,导致自己只动手实践了视频中的一小部分内容。为了赶时间,我打算先把与CNN相关的视频过一遍。然后尽快开始做自己的项目。明天继续加油,争取把Lesson3和Lesson4看完。
- 推荐3家毕业AI论文可五分钟一键生成!文末附免费教程!
小猪包333
写论文人工智能AI写作深度学习计算机视觉
在当前的学术研究和写作领域,AI论文生成器已经成为许多研究人员和学生的重要工具。这些工具不仅能够帮助用户快速生成高质量的论文内容,还能进行内容优化、查重和排版等操作。以下是三款值得推荐的AI论文生成器:千笔-AIPassPaper、懒人论文以及AIPaperPass。千笔-AIPassPaper千笔-AIPassPaper是一款基于深度学习和自然语言处理技术的AI写作助手,旨在帮助用户快速生成高质
- 【自动化测试】UI自动化的分类、如何选择合适的自动化测试工具以及其中appium的设计理念、引擎和引擎如何工作
Lossya
ui自动化测试工具自动化测试appium
引言UI自动化测试主要针对软件的用户界面进行测试,以确保用户界面元素的交互和功能符合预期文章目录引言一、UI自动化的分类1.1基于代码的自动化测试1.2基于录制/回放的自动化测试1.3基于框架的自动化测试1.4按测试对象分类1.5按测试层次分类1.6按测试执行方式分类1.7按测试目的分类二、如何选择合适的自动化测试工具2.1项目需求分析2.2工具特性评估2.3成本考虑2.4团队技能2.5试用和评估
- AI大模型的架构演进与最新发展
季风泯灭的季节
AI大模型应用技术二人工智能架构
随着深度学习的发展,AI大模型(LargeLanguageModels,LLMs)在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进,包括从Transformer的提出到GPT、BERT、T5等模型的历史演变,并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍:Transformer的核心原理Transformer架构的背景在Transfo
- ai绘画工具midjourney怎么下载?附作品管理教程
设计师早上好
Midjourney是一款功能强大的AI绘画工具,它使用机器学习技术和深度神经网络等算法,可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么,ai绘画工具midjourney怎么下载?本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单,只需打开Midjourney官网(点击“GetMidjour
- 性格小测试
熹大头
有些人非常肯定自己属于外向型,有些人则发现自己是绝对的内向型。然而,多数人却发现他们似乎介于两者之间,是两种性格的结合。现在我们就来看看你在这种分类中处在何种位置。阅读以下问题,从a、b、c中选出最适合自己的选项。你可能会发现三个选项都不合适,或者合适的不止一项,这种情况下,选出相对来说更适合自己的即可。1人们经常会用下列哪个词语描述你:a善于分析b遵守纪律c有创造力2一连几天参与社交活动(比如,
- 李克富 | 咨询师推荐阅读书目
李克富
最重要的书籍不是别人的推荐,而是自己学过的教材,不论当初使用的是哪个版本,它都是我们专业的底层代码,具有不可替代性。前不久,中国心理咨询师筹委会的一位老师邀请我罗列一个推荐书目清单作为咨询师工具包的内容,并要求“说明一下简单的分类或者作三言两语的说明”。斟酌后,我觉得自己推荐的书目大体可以分为普及类书籍、心理学书籍和心理咨询与治疗专业书籍,第三类又分为适合于咨询师新手的和有经验咨询师的。经过严格筛
- [实践应用] 深度学习之模型性能评估指标
YuanDaima2048
深度学习工具使用深度学习人工智能损失函数性能评估pytorchpython机器学习
文章总览:YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域,评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标:准确率(
- [实践应用] 深度学习之优化器
YuanDaima2048
深度学习工具使用pytorch深度学习人工智能机器学习python优化器
文章总览:YuanDaiMa2048博客文章总览深度学习之优化器1.随机梯度下降(SGD)2.动量优化(Momentum)3.自适应梯度(Adagrad)4.自适应矩估计(Adam)5.RMSprop总结其他介绍在深度学习中,优化器用于更新模型的参数,以最小化损失函数。常见的优化函数有很多种,下面是几种主流的优化器及其特点、原理和PyTorch实现:1.随机梯度下降(SGD)原理:随机梯度下降通过
- 新能源汽车 BMS 学习笔记篇—BMS 基本定义及分类
WPG大大通
其他笔记汽车BMS经验分享新能源电池
一、BMS定义1、概念:BMS(BatteryManagementSystem)即电池管理系统,其管理对象是二次电池(充电电池或蓄电池),其主要目的是电池的利用率,防止电池出现过度充电和过度放电,可应用于电动汽车、电瓶车、机器人、无人机等图片来源:腾讯网https://new.qq.com《标准普尔警告,电动汽车电池生产面临供应链和地缘政治风险》2、四大功能①感知和测量:检测电池的电压、电流、温度
- 生成式地图制图
Bwywb_3
深度学习机器学习深度学习生成对抗网络
生成式地图制图(GenerativeCartography)是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统(GIS)技术与现代生成模型(如深度学习、GANs等),能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点:自动化生成:通过算法和模型,系统能够根据输入的地理或空间数据自动生成地图,而无需人工逐
- 郭生白中药方论之二(破除温凉寒热的框框)
本能学堂a昨年
离病说药茫茫然,对症下药不着边。顺势利导一乘法,排异调节渡法船。无限整合非模糊,模糊病区得清楚。共性之外求个性,亲和不生抗药性。温凉寒热巧方便,君臣佐使筏喻焉。药包大小折中看,毒性有无一念间。导读破除温凉寒热的框框寒热温凉是基于中药共性的传统分类药无寒热人有寒热药无寒热病有寒热抛弃温凉不并用的错误观念寒热温凉是基于中药共性的传统分类寒热温凉是个共性,是说的共性。这个共性,知道什么叫共性吗?所有的药
- 2022-04-25
L是木子李呢
上门维修APP开发应具备哪些功能随着移动互联网的不断发展,上门维修在我们生活中已经是非常普遍的存在了,为了给用户更方便的找到上门维修的渠道,上门维修APP应运而生,那么上门维修APP开发应具备哪些功能呢?1、维修门店搜索为了更好地方便用户省时省力,上门维修APP会依据用户定位信息搜索线下实体店,促使用户更好的找到线下维修店面,省时又省力。2、维修服务分类包括管道洁具维修、强电弱电维修、木工维修、粉
- 吴恩达深度学习笔记(30)-正则化的解释
极客Array
正则化(Regularization)深度学习可能存在过拟合问题——高方差,有两个解决方法,一个是正则化,另一个是准备更多的数据,这是非常可靠的方法,但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高,但正则化通常有助于避免过拟合或减少你的网络误差。如果你怀疑神经网络过度拟合了数据,即存在高方差问题,那么最先想到的方法可能是正则化,另一个解决高方差的方法就是准备更多数据,这也是非常
- 个人学习笔记7-6:动手学深度学习pytorch版-李沐
浪子L
深度学习深度学习笔记计算机视觉python人工智能神经网络pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络(fullyconvolutionalnetwork,FCN)采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积(transposedconvolution)实现的,输出的类别预测与输入图像在像素级别上具有一一对应关系:通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
- 二十四、k8s 资源管理
繁华依在
k8skubernetes容器云原生
目录一、资源配置范围管理LimitRange介绍1、LimitRange可以做什么:2、资源限制和请求的约束3、创建LimitsRange对象4、示例:创建一个pod5、测试用例测试1:测试2:测试3:二、资源服务质量管理(RequestsQos)1、Qos级别分类:1.1、Guaranteed:1.2、BestEffort:1.3、Burstable:2、Qos的工作特点3、示例三、资源配额管理
- FlagEmbedding
吉小雨
python库python
FlagEmbedding教程FlagEmbedding是一个用于生成文本嵌入(textembeddings)的库,适合处理自然语言处理(NLP)中的各种任务。嵌入(embeddings)是将文本表示为连续向量,能够捕捉语义上的相似性,常用于文本分类、聚类、信息检索等场景。官方文档链接:FlagEmbedding官方GitHub一、FlagEmbedding库概述1.1什么是FlagEmbeddi
- 深度学习-点击率预估-研究论文2024-09-14速读
sp_fyf_2024
深度学习人工智能
深度学习-点击率预估-研究论文2024-09-14速读1.DeepTargetSessionInterestNetworkforClick-ThroughRatePredictionHZhong,JMa,XDuan,SGu,JYao-2024InternationalJointConferenceonNeuralNetworks,2024深度目标会话兴趣网络用于点击率预测摘要:这篇文章提出了一种新
- 分享100个最新免费的高匿HTTP代理IP
mcj8089
代理IP代理服务器匿名代理免费代理IP最新代理IP
推荐两个代理IP网站:
1. 全网代理IP:http://proxy.goubanjia.com/
2. 敲代码免费IP:http://ip.qiaodm.com/
120.198.243.130:80,中国/广东省
58.251.78.71:8088,中国/广东省
183.207.228.22:83,中国/
- mysql高级特性之数据分区
annan211
java数据结构mongodb分区mysql
mysql高级特性
1 以存储引擎的角度分析,分区表和物理表没有区别。是按照一定的规则将数据分别存储的逻辑设计。器底层是由多个物理字表组成。
2 分区的原理
分区表由多个相关的底层表实现,这些底层表也是由句柄对象表示,所以我们可以直接访问各个分区。存储引擎管理分区的各个底层
表和管理普通表一样(所有底层表都必须使用相同的存储引擎),分区表的索引只是
- JS采用正则表达式简单获取URL地址栏参数
chiangfai
js地址栏参数获取
GetUrlParam:function GetUrlParam(param){
var reg = new RegExp("(^|&)"+ param +"=([^&]*)(&|$)");
var r = window.location.search.substr(1).match(reg);
if(r!=null
- 怎样将数据表拷贝到powerdesigner (本地数据库表)
Array_06
powerDesigner
==================================================
1、打开PowerDesigner12,在菜单中按照如下方式进行操作
file->Reverse Engineer->DataBase
点击后,弹出 New Physical Data Model 的对话框
2、在General选项卡中
Model name:模板名字,自
- logbackのhelloworld
飞翔的马甲
日志logback
一、概述
1.日志是啥?
当我是个逗比的时候我是这么理解的:log.debug()代替了system.out.print();
当我项目工作时,以为是一堆得.log文件。
这两天项目发布新版本,比较轻松,决定好好地研究下日志以及logback。
传送门1:日志的作用与方法:
http://www.infoq.com/cn/articles/why-and-how-log
上面的作
- 新浪微博爬虫模拟登陆
随意而生
新浪微博
转载自:http://hi.baidu.com/erliang20088/item/251db4b040b8ce58ba0e1235
近来由于毕设需要,重新修改了新浪微博爬虫废了不少劲,希望下边的总结能够帮助后来的同学们。
现行版的模拟登陆与以前相比,最大的改动在于cookie获取时候的模拟url的请求
- synchronized
香水浓
javathread
Java语言的关键字,可用来给对象和方法或者代码块加锁,当它锁定一个方法或者一个代码块的时候,同一时刻最多只有一个线程执行这段代码。当两个并发线程访问同一个对象object中的这个加锁同步代码块时,一个时间内只能有一个线程得到执行。另一个线程必须等待当前线程执行完这个代码块以后才能执行该代码块。然而,当一个线程访问object的一个加锁代码块时,另一个线程仍然
- maven 简单实用教程
AdyZhang
maven
1. Maven介绍 1.1. 简介 java编写的用于构建系统的自动化工具。目前版本是2.0.9,注意maven2和maven1有很大区别,阅读第三方文档时需要区分版本。 1.2. Maven资源 见官方网站;The 5 minute test,官方简易入门文档;Getting Started Tutorial,官方入门文档;Build Coo
- Android 通过 intent传值获得null
aijuans
android
我在通过intent 获得传递兑现过的时候报错,空指针,我是getMap方法进行传值,代码如下 1 2 3 4 5 6 7 8 9
public
void
getMap(View view){
Intent i =
- apache 做代理 报如下错误:The proxy server received an invalid response from an upstream
baalwolf
response
网站配置是apache+tomcat,tomcat没有报错,apache报错是:
The proxy server received an invalid response from an upstream server. The proxy server could not handle the request GET /. Reason: Error reading fr
- Tomcat6 内存和线程配置
BigBird2012
tomcat6
1、修改启动时内存参数、并指定JVM时区 (在windows server 2008 下时间少了8个小时)
在Tomcat上运行j2ee项目代码时,经常会出现内存溢出的情况,解决办法是在系统参数中增加系统参数:
window下, 在catalina.bat最前面
set JAVA_OPTS=-XX:PermSize=64M -XX:MaxPermSize=128m -Xms5
- Karam与TDD
bijian1013
KaramTDD
一.TDD
测试驱动开发(Test-Driven Development,TDD)是一种敏捷(AGILE)开发方法论,它把开发流程倒转了过来,在进行代码实现之前,首先保证编写测试用例,从而用测试来驱动开发(而不是把测试作为一项验证工具来使用)。
TDD的原则很简单:
a.只有当某个
- [Zookeeper学习笔记之七]Zookeeper源代码分析之Zookeeper.States
bit1129
zookeeper
public enum States {
CONNECTING, //Zookeeper服务器不可用,客户端处于尝试链接状态
ASSOCIATING, //???
CONNECTED, //链接建立,可以与Zookeeper服务器正常通信
CONNECTEDREADONLY, //处于只读状态的链接状态,只读模式可以在
- 【Scala十四】Scala核心八:闭包
bit1129
scala
Free variable A free variable of an expression is a variable that’s used inside the expression but not defined inside the expression. For instance, in the function literal expression (x: Int) => (x
- android发送json并解析返回json
ronin47
android
package com.http.test;
import org.apache.http.HttpResponse;
import org.apache.http.HttpStatus;
import org.apache.http.client.HttpClient;
import org.apache.http.client.methods.HttpGet;
import
- 一份IT实习生的总结
brotherlamp
PHPphp资料php教程php培训php视频
今天突然发现在不知不觉中自己已经实习了 3 个月了,现在可能不算是真正意义上的实习吧,因为现在自己才大三,在这边撸代码的同时还要考虑到学校的功课跟期末考试。让我震惊的是,我完全想不到在这 3 个月里我到底学到了什么,这是一件多么悲催的事情啊。同时我对我应该 get 到什么新技能也很迷茫。所以今晚还是总结下把,让自己在接下来的实习生活有更加明确的方向。最后感谢工作室给我们几个人这个机会让我们提前出来
- 据说是2012年10月人人网校招的一道笔试题-给出一个重物重量为X,另外提供的小砝码重量分别为1,3,9。。。3^N。 将重物放到天平左侧,问在两边如何添加砝码
bylijinnan
java
public class ScalesBalance {
/**
* 题目:
* 给出一个重物重量为X,另外提供的小砝码重量分别为1,3,9。。。3^N。 (假设N无限大,但一种重量的砝码只有一个)
* 将重物放到天平左侧,问在两边如何添加砝码使两边平衡
*
* 分析:
* 三进制
* 我们约定括号表示里面的数是三进制,例如 47=(1202
- dom4j最常用最简单的方法
chiangfai
dom4j
要使用dom4j读写XML文档,需要先下载dom4j包,dom4j官方网站在 http://www.dom4j.org/目前最新dom4j包下载地址:http://nchc.dl.sourceforge.net/sourceforge/dom4j/dom4j-1.6.1.zip
解开后有两个包,仅操作XML文档的话把dom4j-1.6.1.jar加入工程就可以了,如果需要使用XPath的话还需要
- 简单HBase笔记
chenchao051
hbase
一、Client-side write buffer 客户端缓存请求 描述:可以缓存客户端的请求,以此来减少RPC的次数,但是缓存只是被存在一个ArrayList中,所以多线程访问时不安全的。 可以使用getWriteBuffer()方法来取得客户端缓存中的数据。 默认关闭。 二、Scan的Caching 描述: next( )方法请求一行就要使用一次RPC,即使
- mysqldump导出时出现when doing LOCK TABLES
daizj
mysqlmysqdump导数据
执行 mysqldump -uxxx -pxxx -hxxx -Pxxxx database tablename > tablename.sql
导出表时,会报
mysqldump: Got error: 1044: Access denied for user 'xxx'@'xxx' to database 'xxx' when doing LOCK TABLES
解决
- CSS渲染原理
dcj3sjt126com
Web
从事Web前端开发的人都与CSS打交道很多,有的人也许不知道css是怎么去工作的,写出来的css浏览器是怎么样去解析的呢?当这个成为我们提高css水平的一个瓶颈时,是否应该多了解一下呢?
一、浏览器的发展与CSS
- 《阿甘正传》台词
dcj3sjt126com
Part Ⅰ:
《阿甘正传》Forrest Gump经典中英文对白
Forrest: Hello! My names Forrest. Forrest Gump. You wanna Chocolate? I could eat about a million and a half othese. My momma always said life was like a box ochocol
- Java处理JSON
dyy_gusi
json
Json在数据传输中很好用,原因是JSON 比 XML 更小、更快,更易解析。
在Java程序中,如何使用处理JSON,现在有很多工具可以处理,比较流行常用的是google的gson和alibaba的fastjson,具体使用如下:
1、读取json然后处理
class ReadJSON
{
public static void main(String[] args)
- win7下nginx和php的配置
geeksun
nginx
1. 安装包准备
nginx : 从nginx.org下载nginx-1.8.0.zip
php: 从php.net下载php-5.6.10-Win32-VC11-x64.zip, php是免安装文件。
RunHiddenConsole: 用于隐藏命令行窗口
2. 配置
# java用8080端口做应用服务器,nginx反向代理到这个端口即可
p
- 基于2.8版本redis配置文件中文解释
hongtoushizi
redis
转载自: http://wangwei007.blog.51cto.com/68019/1548167
在Redis中直接启动redis-server服务时, 采用的是默认的配置文件。采用redis-server xxx.conf 这样的方式可以按照指定的配置文件来运行Redis服务。下面是Redis2.8.9的配置文
- 第五章 常用Lua开发库3-模板渲染
jinnianshilongnian
nginxlua
动态web网页开发是Web开发中一个常见的场景,比如像京东商品详情页,其页面逻辑是非常复杂的,需要使用模板技术来实现。而Lua中也有许多模板引擎,如目前我在使用的lua-resty-template,可以渲染很复杂的页面,借助LuaJIT其性能也是可以接受的。
如果学习过JavaEE中的servlet和JSP的话,应该知道JSP模板最终会被翻译成Servlet来执行;而lua-r
- JZSearch大数据搜索引擎
颠覆者
JavaScript
系统简介:
大数据的特点有四个层面:第一,数据体量巨大。从TB级别,跃升到PB级别;第二,数据类型繁多。网络日志、视频、图片、地理位置信息等等。第三,价值密度低。以视频为例,连续不间断监控过程中,可能有用的数据仅仅有一两秒。第四,处理速度快。最后这一点也是和传统的数据挖掘技术有着本质的不同。业界将其归纳为4个“V”——Volume,Variety,Value,Velocity。大数据搜索引
- 10招让你成为杰出的Java程序员
pda158
java编程框架
如果你是一个热衷于技术的
Java 程序员, 那么下面的 10 个要点可以让你在众多 Java 开发人员中脱颖而出。
1. 拥有扎实的基础和深刻理解 OO 原则 对于 Java 程序员,深刻理解 Object Oriented Programming(面向对象编程)这一概念是必须的。没有 OOPS 的坚实基础,就领会不了像 Java 这些面向对象编程语言
- tomcat之oracle连接池配置
小网客
oracle
tomcat版本7.0
配置oracle连接池方式:
修改tomcat的server.xml配置文件:
<GlobalNamingResources>
<Resource name="utermdatasource" auth="Container"
type="javax.sql.DataSou
- Oracle 分页算法汇总
vipbooks
oraclesql算法.net
这是我找到的一些关于Oracle分页的算法,大家那里还有没有其他好的算法没?我们大家一起分享一下!
-- Oracle 分页算法一
select * from (
select page.*,rownum rn from (select * from help) page
-- 20 = (currentPag