ARAP参数化算法

ARAP参数化算法实现

综述

三维模型的参数化把三维模型映射到二维平面，LSCM在映射的过程中尽可能地保持三角形的角度相同，ARAP参数化算法在LSCM的基础上尽可能的保证三角形没有扭曲地映射在二维平面上。

算法设计

因为需要映射过程中尽可能保持三角形没有扭曲，所有发生变换的矩阵为旋转矩阵。我们可以通过限制变换矩阵，得到相应参数化结果。

假设三维模型上的一个三角形$t$表示为$x_t=${$x_t^0,x_t^1,x_t^2$}，相应的映射后的三角形表示为$u_t$={$u_t^0,u_t^1,u_t^2$}。这两个三角形之间的关系可以用一个2×2的雅可比（Jobabian）矩阵$J_t(u)$来表示。

用$L_t$来表示受到限制的变换矩阵，也就是旋转变换矩阵，可以定义如下的能量函数来表示可能的变换和目标变换之间的差别：
$$E(u,L)=\sum _{t=1}^T{A}_t||J_t(u)-L_t|{|}_F^2$$
其中$A_t$是三角形的面积。能量函数也可以重构为：
$$\begin{gathered} E(u,L)=\frac{1}{2}\sum _{t=1}^T\sum _{i=0}^{2}cot({\theta }_t^i)||(u_t^i-u_t^{i+1})-L_t(x_t^i-x_t^{i+1})|{|}^2 \\ =\frac{1}{2}\sum _{(i,j)\in halfedge}cot({\theta }_{ij})||(u_i-u_j)-L_{t(i,j)}(x_i-x_j)|{|}^2 \end{gathered}$$
求解能量函数的最小值，对其进行求导
$$\begin{gathered} \sum _{j\in N(i)}[cot({\theta }_{ij})+cot({\theta }_{ij})](u_i-u_j)=\sum _{j\in N(i)}[cot({\theta }_{ij})L_{t(i,j)}+cot({\theta }_{ji})L_{t(j,i)}](x_i-x_j) \\ (i=1,...,n) \end{gathered}$$

其中${\theta }_{ij}$是与边相对的角度，在上面的公式中，未知数为二维平面上的映射的顶点$u$与变换矩阵$L$。

因此参数化算法构造为一个如下的优化问题：
$$(u,t)=argmi{n}_{(}u,t)E(u,t),L_t\in M$$

因为$L_t$限制为旋转矩阵（等距变换矩阵），形式如下：
$$M=\left(\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right):\theta \in [0,2\pi )$$

针对该能量函数有两个未知量，不太好求解，基本思路分为两个步骤求解：

1. local phase：固定所有的$u$，求出每个三角形对应的最佳旋转矩阵$L_t$

   使用LSCM算法得到的二维坐标初始化$U$

   对于如下的2×2矩阵：
   $$S_t(u)=\sum _{i=0}^{2}cot({\theta }_t^i)(u_t^i-u_t^{i+1})(x_t^i-x_t^{i+1})$$
   可以做SVD分解为：
   $$J=U\sum V^T$$
   其中
   $$\sum =\left(\begin{array}{cc}{\sigma }_1& 0\\ 0& {\sigma }_2\end{array}\right)$$
   那么可以得到最佳的变换矩阵：
   $$L=U{V}^T$$
   参考：SVD分解求变换矩阵

2. global phase：固定每个三角形对应的旋转矩阵，求解最佳的U

   通过上一步将求解的$L$代入上述求解能量方程最小值的线性系统中，求解$U$

   方程左侧为固定矩阵，可以构建线性矩阵$AX=B$（A矩阵构建方法参考另一篇博客）

   B矩阵为$n\times 2$的矩阵，在相应的行上修改值。

3. 重复迭代以上的两个步骤，直到能量变化不明显

算法结果

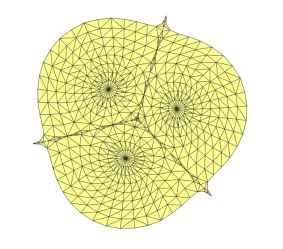
初始模型	LSCM	ARAP

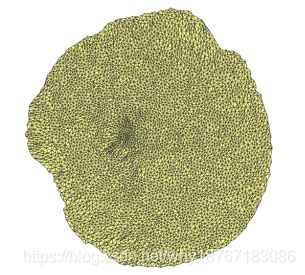从实验结果可以看出ARAP在尽可能保持三角形角度不变的同时保证三角形不发生扭曲。

代码

//用LACM算法得到初始的参数化坐标作为初始值
void MeshViewerWidget::InitUV() {
	Mesh mesh1=Parameterize();
	vt.resize(v_count);
	for (int i = 0; i < v_count; i++) {
		vt[i][0] = New_U[i];
		vt[i][1] = New_V[i];
	}
}

//计算每个点的cot
void MeshViewerWidget::CalCots() {
	Cots.resize(f_count);
	W.resize(v_count);

	for (int k = 0; k < f_count; ++k) {
		Cots[k].resize(3);//每行为3列
		
	}
	for (int k = 0; k < v_count; k++) {
		W[k].resize(v_count);
	}

	//遍历所有的面
	for (auto f_it = mesh.faces_begin(); f_it != mesh.faces_end(); f_it++) {
		vector<int> v(3, 0);
		int i = 0;
		for (auto fv_it = mesh.fv_iter(*f_it); fv_it.is_valid(); ++fv_it) {  //遍历该面的所有点
			v[i] = (*fv_it).idx();   //保存该面顶点编号
			i++;
		}
		//计算3条边的边长
		double a, b, c;
		a = (mesh.point((mesh.vertex_handle(v[0]))) - mesh.point((mesh.vertex_handle(v[1])))).length();
		b = (mesh.point((mesh.vertex_handle(v[1]))) - mesh.point((mesh.vertex_handle(v[2])))).length();
		c = (mesh.point((mesh.vertex_handle(v[2]))) - mesh.point((mesh.vertex_handle(v[0])))).length();
		double angle1 = acos((a*a + c * c - b * b) / (2 * a*c));
		double angle2 = acos((a*a + b * b - c * c) / (2 * a*b));
		double angle3 = acos((b*b + c * c - a * a) / (2 * b*c));		
		Cots[(*f_it).idx()][0] = 1.0 / tan(angle1);
		Cots[(*f_it).idx()][1] = 1.0 / tan(angle2);
		Cots[(*f_it).idx()][2] = 1.0 / tan(angle3);		
		W[v[1]][v[2]] = 1.0 / tan(angle1);
		W[v[2]][v[0]] = 1.0 / tan(angle2);
		W[v[0]][v[1]] = 1.0 / tan(angle3);
	}
}

//对于每个三角形计算参数化之前和参数化之后的变换矩阵
Eigen::Matrix3d MeshViewerWidget::ComputeTransformMatrix(Mesh::FaceIter face) {
	Eigen::Vector2d u[3];
	int face_id = (*face).idx();
	int i = 0;
	for (auto fv_it = mesh.fv_iter(*face); fv_it.is_valid(); ++fv_it) {  //遍历面上的所有点
		u[i] = vt[(*fv_it).idx()];
		i++;
	}
	Eigen::MatrixXd uu, xx, cc;
	uu.resize(3, 3);
	xx.resize(3, 3);
	cc.resize(3, 3);
	for (int i = 0; i < 3; i++) {
		for (int j = 0; j < 3; j++) {
			uu(i, j) = 0.0;
			xx(i, j) = 0.0;
			cc(i, j) = 0.0;
		}
	}
	for (i = 0; i < 3; i++) {
		int n = (i + 1) % 3;
		int p = (i + 2) % 3;
		uu(i, 0) = u[p][0] - u[n][0];
		uu(i, 1) = u[p][1] - u[n][1];
		xx(i, 0) = edgeVectors[face_id][i][0];
		xx(i, 1) = edgeVectors[face_id][i][1];
		cc(i, i) = Cots[face_id][i];

	}
	Eigen::Matrix3d CovMat = xx.transpose() * cc * uu;
	return CovMat;
}

//对每个三角形点的变换矩阵用SVD分解方法计算变换矩阵的旋转部分
Eigen::Matrix3d MeshViewerWidget::SVD(Eigen::Matrix3d CovMat) {
	JacobiSVD<Eigen::MatrixXd> svd(CovMat, ComputeThinU | ComputeThinV);
	Matrix3d V = svd.matrixV(), U = svd.matrixU();
	Matrix3d rot = V * U.transpose();
	if (rot.determinant() < 0) {
		if (svd.singularValues()[0] < svd.singularValues()[1]) {
			for (int i = 0; i < 2; i++) {
				U(i,0) = -1 * U(i,0);
				
			}
		}
		else {
			for (int i = 0; i < 2; i++) {
				U(i, 1) = -1 * U(i, 1);
				
			}
		}
		rot = V * U.transpose();
	}
	return rot;
}

//计算所有三角形的旋转矩阵
vector < Eigen::Matrix2d> MeshViewerWidget::ARAPLocal() {
	vector < Eigen::Matrix2d> R(f_count);
	for (auto f_it = mesh.faces_begin(); f_it != mesh.faces_end(); f_it++) {
		Eigen::Matrix3d CovMat = ComputeTransformMatrix(f_it);
		Eigen::Matrix3d rot = SVD(CovMat);
		R[(*f_it).idx()] << rot(0, 0), rot(0, 1),
			rot(1, 0), rot(1, 1);

	}
	
	return R;
}

//计算拉普拉斯矩阵L
void MeshViewerWidget::Laplacian() {
	Eigen::SparseMatrix<double> D, M;
	M.resize(v_count, v_count);
	std::vector<Eigen::Triplet<double>> tripletlist_M;
	for (auto v_it = mesh.vertices_begin(); v_it != mesh.vertices_end(); v_it++) {
		int v_idx = (*v_it).idx();
		double w = 0;
		for (auto vv_it = mesh.vv_begin(*v_it); vv_it.is_valid(); ++vv_it) {
			int vv_idx = (*vv_it).idx();
			w += W[v_idx][vv_idx] + W[vv_idx][v_idx];
			tripletlist_M.push_back(Eigen::Triplet<double>(v_idx, vv_idx, W[v_idx][vv_idx] + W[vv_idx][v_idx]));
			
		}
		tripletlist_M.push_back(Eigen::Triplet<double>(v_idx, v_idx,-1.0 * w));
	}
	M.setFromTriplets(tripletlist_M.begin(), tripletlist_M.end());
	// L = D * M;
	L = M;
}

void MeshViewerWidget::ARAPGlobal(vector < Eigen::Matrix2d> R) {
	Eigen::MatrixXd b_xy;
	b_xy.resize(v_count, 2);
	for (int i = 0; i < v_count; i++) {
		b_xy(i, 0) = 0.0;
		b_xy(i, 1) = 0.0;
	}
	for (auto f_it = mesh.faces_begin(); f_it != mesh.faces_end(); f_it++) {
		int face_idx = (*f_it).idx();
		vector<int> v(3, 0);
		int i = 0;
		for (auto fv_it = mesh.fv_iter(*f_it); fv_it.is_valid(); ++fv_it) {  //遍历该面的所有点
			v[i] = (*fv_it).idx();   //保存该面顶点编号
			i++;
		}
		for (i = 0; i < 3; i++) {
			int n = (i + 1) % 3;
			int p = (i + 2) % 3;
			Eigen::Vector2d E_ij = edgeVectors[face_idx][i];
			//Eigen::Vector2d b = R[face_idx] * E_ij * Cots[face_idx][i];
			Eigen::Vector2d b = Cots[face_idx][i] * R[face_idx] *  E_ij  ;
			b_xy(v[n], 0) -= b[0];
			b_xy(v[p], 0) += b[0];
			b_xy(v[n], 1) -= b[1];
			b_xy(v[p], 1) += b[1];
			
		}
	}
	Eigen::LeastSquaresConjugateGradient<Eigen::SparseMatrix<double> > bxy_Solver_sparse;
	bxy_Solver_sparse.compute(L);

	Eigen::SparseMatrix<double> Bxy_Sparse;
	Bxy_Sparse.resize(v_count, 2);
	buildSparseMatrix(Bxy_Sparse, b_xy, v_count, 2);
	Eigen::MatrixXd U_xy;
	U_xy.resize(v_count, 2);
	U_xy = bxy_Solver_sparse.solve(Bxy_Sparse);
	for (int i = 0; i < v_count; i++) {
		vt[i][0] = U_xy(i, 0);
		vt[i][1] = U_xy(i, 1);
	}

}

double MeshViewerWidget::CalEdgeVectors(vector < Eigen::Matrix2d> R) {
	double E = 0;
	for (auto f_it = mesh.faces_begin(); f_it != mesh.faces_end(); f_it++) {
		int face_idx = (*f_it).idx();
		vector<int> v(3, 0);
		int i = 0;
		for (auto fv_it = mesh.fv_iter(*f_it); fv_it.is_valid(); ++fv_it) {  //遍历该面的所有点
			v[i] = (*fv_it).idx();   //保存该面顶点编号
			i++;
		}
		for (i = 0; i < 3; i++) {
			int n = (i + 1) % 3;
			int p = (i + 2) % 3;
			Eigen::Vector2d U_ij = vt[v[p]] - vt[v[n]];
			Eigen::Vector2d E_ij = edgeVectors[face_idx][i];
			E += pow(Cots[face_idx][i] * (U_ij - R[face_idx] * E_ij).norm(), 2);
		}
		return E;
	}
	return E;
}
Mesh MeshViewerWidget::ARAP() {
	InitUV();
	//edgeVectors;
	CalCots();  //计算每个三角面的顶点对应的cot
	Laplacian();

	double E = -1;
	double Epre = 0;
	int iterations = 0;
	cout << endl << endl << endl;
	while (abs(Epre - E) >0.01 )
	{
		cout << "iterations:                 " << iterations << endl;
		iterations++;
		Epre = E;
		vector < Eigen::Matrix2d> R;
		R=ARAPLocal();
		ARAPGlobal(R);
		E=CalEdgeVectors(R);

		if (iterations > 3) break;

	}
	Mesh temp;
	Mesh::VertexHandle *vhandle;    //点的迭代器指针

	vhandle = new Mesh::VertexHandle[mesh.n_vertices()];  //开辟的空间大小

	for (auto v_it = mesh.vertices_begin(); v_it != mesh.vertices_end(); ++v_it) {   //遍历每个点，将每个点对应的2D坐标加入temp
		vhandle[(*v_it).idx()] = temp.add_vertex(Mesh::Point(vt[(*v_it).idx()][0], vt[(*v_it).idx()][1], 0));
	}
	for (auto f_it = mesh.faces_begin(); f_it != mesh.faces_end(); ++f_it) {   //遍历每个面
		std::vector<Mesh::VertexHandle>  face_vhandles;   //存放2D的每个三角形平面
		for (auto fv_it = mesh.fv_iter(*f_it); fv_it.is_valid(); ++fv_it) {  //遍历该面的所有点
			face_vhandles.push_back(vhandle[(*fv_it).idx()]);  //通过vhandle将3D的点转化到2D平面上
		}
		temp.add_face(face_vhandles);
	}
	return temp;
}

参考文献

[1] Liu L, Zhang L, Xu Y, et al. A local/global approach to mesh parameterization[C]. symposium on geometry processing, 2008, 27(5): 1495-1504.

[2] Sorkine O, Alexa M. As-rigid-as-possible surface modeling[C]. symposium on geometry processing, 2007: 109-116.

[3] Least-Squares Rigid Motion Using SVD

[4] https://blog.csdn.net/why18767183086/article/details/108002084