11.数据结构:认识一棵树
大家好,我是王有志。关注王有志,回复DSA获取数据结构和算法学习资源。
今天我们要学习的是你编程生涯中不可避免的话题–树,无论是二分搜索树,红黑树,B+树,还是机器学习中的决策树和随机森林,都和树息息相关。
认识一棵树
按照惯例,我会把树的定义放上来,这次也不例外:
树是n(n≥0)个节点的有限集,当n=0时被称为空树。在任意一棵非空树中:
(1)有且仅有一个特定的节点称为根(Root)节点;
(2)当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2…Tn,其中每个集合本身也是一棵树,且称为根的子树(SubTree)。
定义看起来可能会有些晕,下面我们通过一张多叉树的图来理解树中的概念和定义:
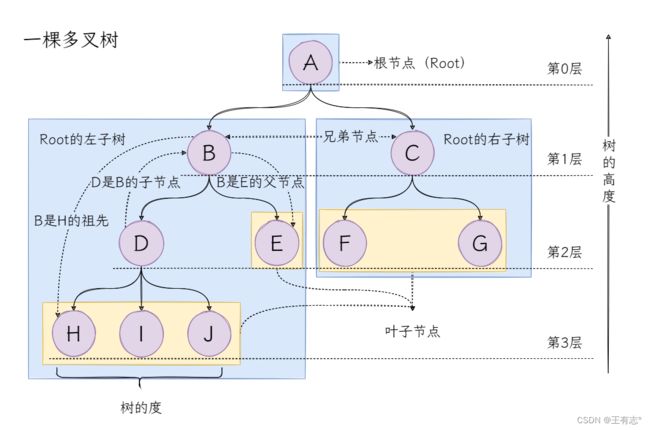
结合定义,相信你已经理解了大部分的概念和定义,那么我们再补充一点点关于树的度的定义。
在树中节点的度指的是节点拥有的子节点的个数,例如,节点B的度是2,节点D的度是3,而树的度指的是树中度最大的节点的度。这么说可能有些拗口,通俗点讲就是,哪个节点拥有最多的子节点,它的子节点个数就是树的度。
二叉树的分类
如果我们按照树的度进行分类,那么树只有两类:二叉树和多叉树。
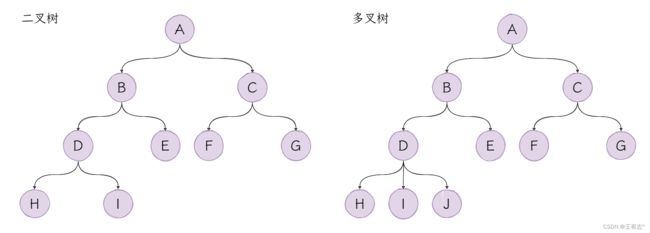
树的度小于等于2的称为二叉树,大于2的称为多叉树。
满二叉树
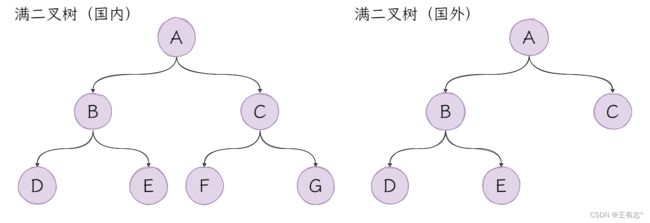
对于满二叉树,国内外的定义有些许的差异:
国内定义为,一棵二叉树中,每层节点的个数都达到最大值,就是满二叉树。即深度为 k k k的二叉树,节点个数为 2 k − 1 2^k -1 2k−1。
国外定义为,一棵二叉树中,非叶子节点都有两个子节点,就是满二叉树。区别在于,国内的定义要求每层节点个数都是满的。
完全二叉树
对于一棵二叉树,如果将其每个节点进行从上到下,从左到右依次编号,可以与满二叉树重合,就是完全二叉树。从定义上看,完全二叉树是满二叉树的其中一类子集。
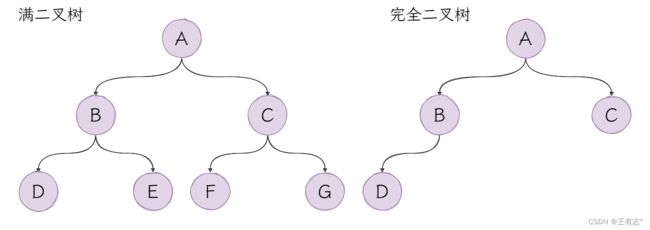
可以看到,完全二叉树并不要求每个非叶子节点都有两个子节点,但是要求“有序”。
平衡二叉树
平衡二叉树是左右子树高度差不超过1的二叉树。

如果只从结构上来看,平衡二叉树是完全二叉树。区别在于,我们在实现平衡二叉树时,会添加节点之间的排序关系,因此在构建树平衡二叉树的时候,为了保持这种平衡需要进行旋转。
常见的平衡二叉树有,AVL树,红黑树,替罪羊树等。
斜树
当一棵树只有左/右子节点时,我们称之为左/右斜树。
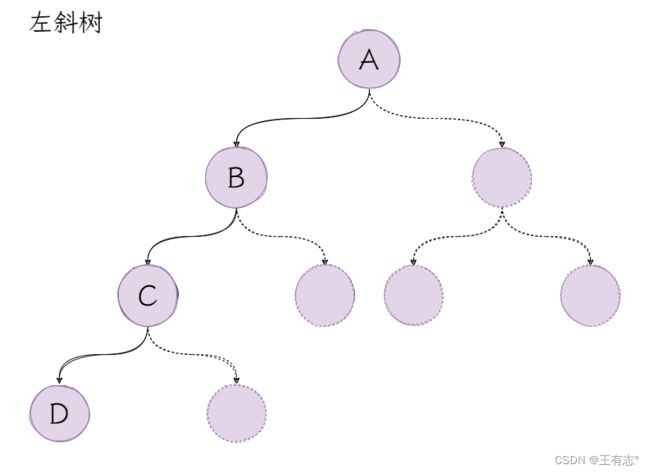
从结构上看,我们也可以认为链表是一种斜树。
二叉树的存储结构
像栈一样,我们也可以实现顺序结构的二叉树或者链式结构的二叉树。实际上链表也是可以通过一维数组描述–静态链表,但是没有必要。
静态结构
二叉树也可以通过一维数组描述。

我们有一个存储了8个节点的二叉树,将根节点存储在下标为1的位置,记为 i n d e x _ a index\_a index_a,我们就可以通过简单的计算获的根节点A的左右子节点的下标:
节点A的左子节点(节点B): 2 × i n d e x _ a = 2 2 \times index\_a = 2 2×index_a=2
节点A的右子节点(节点C): 2 × i n d e x _ a + 1 = 3 2 \times index\_a + 1= 3 2×index_a+1=3
同样的我们通过计算可以访问到C的左右子节点:
节点C的左子节点(空节点): 2 × i n d e x _ c = 6 2 \times index\_c = 6 2×index_c=6
节点C的右子节点(节点F): 2 × i n d e x _ c + 1 = 7 2 \times index\_c + 1 = 7 2×index_c+1=7
但是你发现了吗?为了保证公式可用,即便节点C没有左子节点,我们也必须将位置空出来,造成了内存空间的浪费,显然是不够理想的方式。
链式结构
我们也可以创建类似双向链表节点的方式,创建二叉树的节点:
public class TreeNode {
private E element;
private TreeNode leftChild;
private TreeNode rightChild;
}
实际上,这点代码已经可以构建一棵二叉树了。
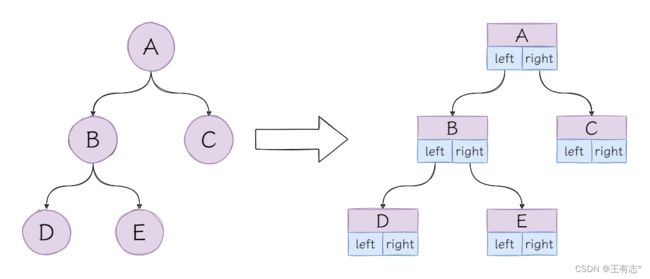
和链表一样,只有TreeNode在使用起来会非常麻烦,要手动实现添加,查找等功能,增加了使用难度。我们可以将功能封装起来只提供接口,不过这不是今天的重点,我们按下不表。
结语
今天我们初步认识了树中的概念和定义,希望通这张图能够让你快速的理解,而不需要死记硬背。
接着我们一起看了4种二叉树结构,这些特殊的结构也是我们学习后面二叉树何种实现的基础。
最后介绍了二叉树的两种存储结构,对于这种动态数据结构通过一维数组的实现方式,我们了解其原理就够了。
你可能会发觉今天画了很多图,是因为我们要学习的数据结构从一维升到了二维,靠想象我已经很难在脑袋中描绘出它们了。
好了,今天就到这里了,Bye~~