吴恩达机器学习第四周学习笔记及编程作业答案
一、理论基础
1. 神经网络
非线性假设
当特征太多时,计算的负荷会非常大,这时可以使用非线性的多项式项,能够帮助我们建立更好的分类模型。
1.1 模型表示
第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(bias unit),偏差单元的值为1
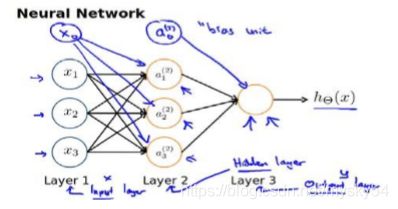
ai(j)代表第j层的第i个激活单元。θ(j)代表从第j层映射到第j+1层时的权重的矩阵,例如(1)代表从第一层映射到第二层的权重的矩阵。其尺寸为:以第 + 1层的激活单元数量为行数,以第 层的激活单元数加一为列数的矩阵。例如:上图所示的神经网络中(1)的尺寸为3*4。
对于上图所示的模型,激活单元和输出分别表达为:
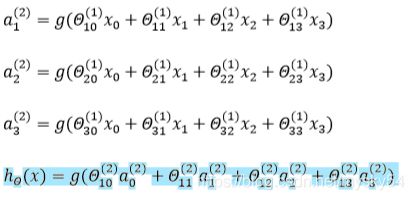
每一个都是由上一层所有的和每一个所对应的决定的
我们把这样从左到右的算法称为前向传播算法(FORWARD PROPAGATION )

神经网络表示 AND 函数:


所以可以得出AND函数:
![]()
OR 函数:
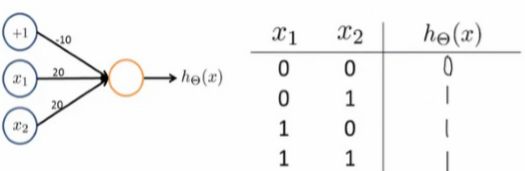
二、编程作业
(一)逻辑回归解决多分类问题
1.lrCostFunction.m(Logistic regression cost function): modify your code in lrCostFunction to account for regularization. Once again, you should not putany loops into your code.
(unregularized) logistic regression cost function:
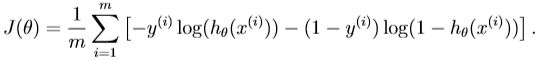
regularized logistic regression cost function:

正则逻辑回归成本的偏导数:
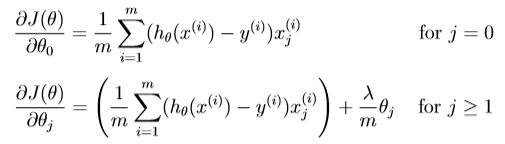
Sigmoid function:
![]()
![]()

注:在这个等式中,我们使用了这样一个事实:如果a和b是向量,则有:
![]()
function [J, grad] = lrCostFunction(theta, X, y, lambda)
% Initialize some useful values
m = length(y); % number of training examples
J = 0;
grad = zeros(size(theta));
%分别计算出代价值J和梯度grad,后部的theta平方里面theta(0)是不参与的,故在程序中theta(1)是不参与的
J = 1 / m * ( -y' * log(sigmoid( X * theta )) - (1 - y)' * log(1 - sigmoid( X * theta ))) + lambda/(2*m)*(theta'*theta -theta(1)^2);
grad = 1 / m * (X' * (sigmoid(X*theta) - y));
temp = theta;
temp(1) = 0;
grad = grad + lambda/m * temp;
grad = grad(:);
end
2.oneVsAll.m(Train a one-vs-all multi-class classifier):implement one-vs-all classification by training multiple regularized logistic regression classifiers, one for each of the K classes in our dataset(Figure 1).
function [all_theta] = oneVsAll(X, y, num_labels, lambda)
m = size(X, 1);%行
n = size(X, 2);%列
all_theta = zeros(num_labels, n + 1); %num_labels为分类器个数,N+1为参数个数,为训练1-10个便签,所以需要矩阵为10*n+1,本题为10×401
% Add ones to the X data matrix
X = [ones(m, 1) X];%在原有矩阵前面附加一列1的向量,因为有常数项,5000×401
%fminunc是一个优化求解器,它可以找到一个未约束函数的最小值
%本题运用了fmincg()函数求参数,与函数fminunc()相比,处理属性过多时更高效!
initial_theta=zeros(n+1,1);%模型参数θ的初始值
%'GradObj' 设置为 'on' ,告诉 fminunc 我们使用的函数同时返回代价(cost)和梯度(gradient),这是的 fminunc 在最小化 cost 时使用我们自己的梯度。
%‘MaxIter' 设置为 50,表示fminunc 在返回之前最多迭代50次
options = optimset('GradObj', 'on', 'MaxIter', 50);
%@为函数句柄,@后面括号里的 t 表示函数的参数,也就是我们所需要求解最小代价的参数θ
for c = 1:num_labels
% 传入 lrCostFunction() 里的 theta 是列向量,所以 all_theta(c,:)',调用fmincg时,theta的初始值为 all_theta(c,:)' ,有转置
theta = fmincg(@(t)(lrCostFunction(t,X,(y==c),lambda)),initial_theta, options);
all_theta(c,:)=theta';
end
end
3.predictOneVsAll.m(Predict using a one-vs-all multi-class classifier)
function p = predictOneVsAll(all_theta, X)
m = size(X, 1);
num_labels = size(all_theta, 1);
p = zeros(size(X, 1), 1);
% Add ones to the X data matrix
X = [ones(m, 1) X];%在原有矩阵前面附加一列1的向量,因为有常数项
% X: 5000 * 401, all_theta: 10 * 401
% X * all_theta': 5000 * 10
[max1, p] = max(X * all_theta', [], 2);
end
注:max(A, [], 2): obtain the max for each row.
(二)神经网络解决多分类问题
4.predict.m(Neural network prediction function)

function p = predict(Theta1, Theta2, X)
% Useful values
m = size(X, 1);
num_labels = size(Theta2, 1);
p = zeros(size(X, 1), 1);
% a1加一列偏置项,值全为1
a1 = [ones(m,1) X];
z2 = a1 * Theta1';
% 计算a2
a2 = sigmoid(z2);
a2添加一列偏置项,值全为1
a2 = [ones(size(z2,1),1) a2];
z3 = a2 * Theta2';
% 计算a3
a3 = sigmoid(z3);
[max2,index] = max(a3, [] , 2);
p = index;
end