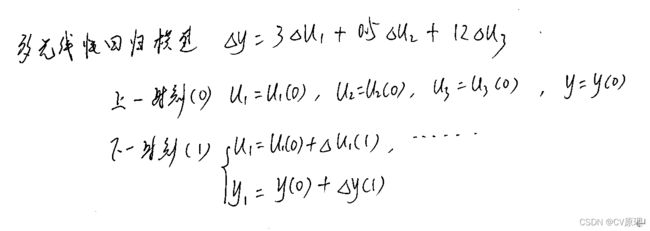一个简单的MPC案例-基于多元线性回归模型
一个简单的MPC案例-基于多元线性回归模型
- 1 多元线性回归模型
- 2 MATLAB代码
-
- 2.1 第一版本
- 2.2 第二版本
- 2.3 第三版本（推荐）
- 3 控制效果
-
- 3.1 第一版本控制效果
- 3.2 第三版本控制效果
- 如有错误，请多指正，希望与大家多多交流！
1 多元线性回归模型
2 MATLAB代码
2.1 第一版本
clc;clear;close all;
%%%% 一个三元线性回归模型，只预测1步
%% 系统初值
u_k0=[5 0.8 11]; %输出初值
y_k0=900; %输入初值
y_k0_history=y_k0; %系统实际输出的历史序列
%% 期望的系统输出值
y_ref1=1000;
%% 目标优化函数各模块的权重
Q=1;
P1=0.1;
P2=0.2;
P3=0.03;
%% 用在滚动优化里，比较法寻找目标函数J的最小值
J_min=1000000000;
%% 控制过程可视化
figure('Name','MPC-基于多元线性回归模型','NumberTitle','off');
%% 滚动优化
for k=1:1:100 %总的时间窗口长度
for delta_u1_k1=-0.1:0.005:0.1 %站在k=0时刻有，计算未来最优控制序列，使用网格法对目标函数寻优
for delta_u2_k1=-0.05:0.001:0.05
for delta_u3_k1=-0.2:0.005:0.2
delta_u_k1=[delta_u1_k1 delta_u2_k1 delta_u3_k1]; %这一次循环，控制量的增量可能的取值
u_k1=u_k0+delta_u_k1; %这一次循环，控制量可能的取值
y_k1_pre=y_k0+[3 0.5 12]*delta_u_k1'; %预测这一次循环，系统的输出
J=(y_ref1-y_k1_pre)*Q*(y_ref1-y_k1_pre)'...
+delta_u1_k1*P1*delta_u1_k1'...
+delta_u2_k1*P2*delta_u2_k1'...
+delta_u3_k1*P2*delta_u3_k1'; % 目标函数
if J<J_min % 比较法，记录最小的J对应的未来控制序列
delta_u_k1_best=delta_u_k1; % 最优控制量增量的序列
u_k1_best=u_k1; % 最优控制量的序列，作用到系统
J_min=J; %记录这一次循环的J值，可能后面有更小的J值
end
end
end
end
y_k1_true=y_k0+[3 0.5 12]*delta_u_k1_best'+3*rand(1,1); % 最优控制量增量的序列，作用到系统，系统实际上可能带有噪声
y_k0=y_k1_true;% 误差反馈校正，把新的时刻系统实际的输出值作为系统初值
y_k0_history=[y_k0_history y_k0];% 记录每个时刻系统实际的输出值，便于画图
plot1=plot(0:1:k,y_k0_history,'r'); %画图
hold on;
plot2=scatter(k,y_k0,'b');
hold on;
legend([plot1,plot2],'系统实际的输出值','系统实际的输出值')
hold on;
pause(0.2);% 时间间隔以下，防止画图太快了，感受不到控制的动态过程
end
2.2 第二版本
clc;clear;close all;
%%%% 一个三元线性回归模型，只预测1步，动态改变系统的输出期望值
%% 系统初值
u_k0=[5 0.8 11]; %输出初值
y_k0=10; %输入初值
y_k0_history=y_k0; %系统实际输出的历史序列
%% 期望的系统输出值
%y_ref1=654;
%% 目标优化函数各模块的权重
Q=1;
P1=0.1;
P2=0.2;
P3=0.03;
%% 用在滚动优化里，比较法寻找目标函数J的最小值
J_last=1000000000;
%% 控制过程可视化
figure('Name','MPC-基于多元线性回归模型','NumberTitle','off');
%% 滚动优化
for k=1:1:300 %总的时间窗口长度
if k<50
y_ref1=20;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(-0.05*(k));
elseif k>=50 && k<120
y_ref1=70;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(-0.05*(k-50));
elseif k>=120 && k<180
y_ref1=50;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(-0.05*(k-120));
elseif k>=180 && k<261
y_ref1=40;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(-0.05*(k-180));
elseif k>=261 && k<301
y_ref1=60;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(-0.05*(k-261));
end
% y_ref11=y_ref1+(y_k0-y_ref1)*exp(-0.05*k);
for delta_u1_k1=-0.1:0.005:0.1 %站在k=0时刻有，计算未来最优控制序列，使用网格法对目标函数寻优
for delta_u2_k1=-0.05:0.001:0.05
for delta_u3_k1=-0.2:0.005:0.2
delta_u_k1=[delta_u1_k1 delta_u2_k1 delta_u3_k1]; %这一次循环，控制量的增量可能的取值
u_k1=u_k0+delta_u_k1; %这一次循环，控制量可能的取值
y_k1_pre=y_k0+[3 0.5 12]*delta_u_k1'; %预测这一次循环，系统的输出
J=(y_ref11-y_k1_pre)*Q*(y_ref11-y_k1_pre)'...
+delta_u1_k1*P1*delta_u1_k1'...
+delta_u2_k1*P2*delta_u2_k1'...
+delta_u3_k1*P2*delta_u3_k1'; % 目标函数
if J<J_last % 比较法，记录最小的J对应的未来控制序列
delta_u_k1_best=delta_u_k1; % 最优控制量增量的序列
u_k1_best=u_k1; % 最优控制量的序列，作用到系统
end
J_last=J; %记录这一次循环的J值，可能后面有更小的J值
end
end
end
y_k1_true=y_k0+[3 0.5 12]*delta_u_k1_best'+2*rand(1,1); % 最优控制量增量的序列，作用到系统，系统实际上可能带有噪声
y_k0=y_k1_true;% 误差反馈校正，把新的时刻系统实际的输出值作为系统初值
y_k0_history=[y_k0_history y_k0];% 记录每个时刻系统实际的输出值，便于画图
plot1=plot(0:1:k,y_k0_history,'r'); %画图
hold on;
plot2=scatter(k,y_k0,'b');
hold on;
plot3=scatter(k,y_ref11,'k','filled');
hold on;
legend([plot1,plot2,plot3],'系统实际的输出值','系统实际的输出值','系统期望的输出值')
hold on;
pause(0.1);% 时间间隔以下，防止画图太快了，感受不到控制的动态过程
end
2.3 第三版本（推荐）
clc;clear;close all;
%%%% 一个三元线性回归模型，只预测1步，动态改变系统的输出期望值，J到了一定值，提前跳出网格寻优
%%%%
%% 系统初值
u_k0=[20 15 11 0]; %控制量初值
u_k0_history=u_k0;
y_k0=50; %被控量初值
y_k0_history=y_k0; %系统实际输出的历史序列
%% 期望的系统输出值
%y_ref1=654;
%% 系统输出的预测模型
Mmodel=[300 -2 120 0.08]; % 最后一个参数是截距项
%% 系统输出含有的噪声
%Noise=0.8*randn(1,1);
%Noise=5*normrnd(0,0.5,1,1); %均值为0，方差为0.5的随机数
Noise=0.5;
%% 目标优化函数各模块的权重
Q=10;
P1=30;
P2=2;
P3=1;
%% 用在滚动优化里，比较法寻找目标函数J的最小值
J_min=100;
%% 控制过程可视化
figure('Name','MPC-基于多元线性回归模型','NumberTitle','off');
%% 滚动优化
y_change_rate=-0.02; %参考轨迹上升到期望值的时间，为负数，越负时间越短
%J_target=0.05;%提前跳出网格寻优的J阈值
J_target=0.05;%提前跳出网格寻优的J阈值
%-----
%记录1：Noise=10; J_target=0.01;发现u2的变化也是敏感的了
%记录2：Noise=0.5; y_change_rate=-0.5; J_target=0.05;发现u1\u2\u3的变化也是敏感的了
%-----
for k=1:1:500 %总的时间窗口长度
if k<50
y_ref1=100;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(y_change_rate*(k));
elseif k>=50 && k<100
y_ref1=150;
%%%%% 到底是用上个时刻的实际值，还是上个阶段的稳态值呢？？？？ 应该是都可以的 现在确定是用上个时刻的实际值
y_ref11=y_ref1+(y_k0-y_ref1)*exp(y_change_rate*(k-50));
%y_ref11=y_ref1+(100-y_ref1)*exp(y_change_rate*(k-50));
elseif k>=100 && k<150
y_ref1=100;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(y_change_rate*(k-100));
%y_ref11=y_ref1+(50-y_ref1)*exp(y_change_rate*(k-100));
elseif k>=150 && k<200
y_ref1=20;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(y_change_rate*(k-150));
elseif k>=200 && k<250
y_ref1=57;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(y_change_rate*(k-200));
elseif k>=250 && k<300
y_ref1=10;
y_ref11=y_ref1+(y_k0-y_ref1)*exp(y_change_rate*(k-250));
end
break_flag_1=0; % 跳出嵌套for循环的标志位
for delta_u1_k1=-1:0.1:1 %站在k=0时刻有，计算未来最优控制序列，使用网格法对目标函数寻优
for delta_u2_k1=-0.5:0.08:0.5
for delta_u3_k1=-0.5:0.005:0.5
delta_u_k1=[delta_u1_k1 delta_u2_k1 delta_u3_k1 1]; %这一次循环，控制量的增量可能的取值
u_k1=u_k0+delta_u_k1; %这一次循环，控制量可能的取值
y_k1_pre=y_k0+Mmodel*delta_u_k1'; %预测这一次循环，系统的输出
J=(y_ref11-y_k1_pre)*Q*(y_ref11-y_k1_pre)'...
+delta_u1_k1*P1*delta_u1_k1'...
+delta_u2_k1*P2*delta_u2_k1'...
+delta_u3_k1*P3*delta_u3_k1';% 目标函数1
J=J/(Q+P1+P2+P3);% 目标函数2，似乎这样更合理？
%J=(y_ref11-y_k1_pre)*Q*(y_ref11-y_k1_pre)';% 目标函数3
if J<=J_target
break_flag_1=1;
delta_u_k1_best=delta_u_k1; % 最优控制量增量的序列
u_k1_best=u_k1; % 最优控制量的序列，作用到系统
y_k1_pre_best=y_k1_pre;
break; % J值小到一定的话，提前跳出网格寻优
elseif J<J_min % 比较法，记录最小的J对应的未来控制序列
delta_u_k1_best=delta_u_k1; % 最优控制量增量的序列
u_k1_best=u_k1; % 最优控制量的序列，作用到系统
y_k1_pre_best=y_k1_pre;
J_min=J; %记录这一次循环的J值，可能后面有更小的J值
end
end
if break_flag_1==1, break; end % 跳出嵌套for循环
end
if break_flag_1==1, break; end % 跳出嵌套for循环
end
% y_k1_true=y_k1_pre_best+Noise*normrnd(0,0.5,1,1); % 最优控制量增量的序列，作用到系统，系统实际上可能带有噪声
y_k1_true=y_k1_pre_best...
+Noise*normrnd(0,0.05,1,1)*...
0.5*normrnd(0,1,1,1)*...
0.7*normrnd(0,1,1,1)*...
0.2*normrnd(0,1,1,1)*...
normrnd(0,1000,1,1)*...
sin(k); % 最优控制量增量的序列，作用到系统，系统实际上可能带有噪声
y_k0=y_k1_true;% 误差反馈校正，把新的时刻系统实际的输出值作为系统初值
y_k0_history=[y_k0_history y_k0];% 记录每个时刻系统实际的输出值，便于画图
%% 命令窗口调试
clc;
% y_k0_history';
% y_ref11-y_k1_pre_best
% (y_ref11-y_k1_pre_best)*Q*(y_ref11-y_k1_pre_best)'
J
u_k1_best
format shortg
c = clock;
fix(c)
%% 可视化
plot_length=150;% 窗口长度
u_k0_history=[u_k0_history;u_k1_best];% 记录每个时刻系统实际的输出值，便于画图
% 点击图形界面， 然后点击任意一个字母按键
pause(0.01); %必须要有这个， 要不然程序可能无法得到你的键盘输入
if isletter(get(gcf,'CurrentCharacter'))
break;
end
subplot(211);
xlim([k-plot_length inf]);
plot1=plot(0:1:k,y_k0_history,'r--'); %画图
hold on;
% plot2=scatter(k,y_k0,'b');
% hold on;
plot2=scatter(k,y_k1_pre_best,'b');
hold on;
plot3=scatter(k,y_ref11,'g','filled');
hold on;
legend([plot1,plot2,plot3],'系统实际的输出值','系统预测的输出值','系统期望的输出值');
hold on;
grid on;
subplot(212);
xlim([k-plot_length inf]);
plot4=stairs(0:1:k,u_k0_history(:,1),'r'); %画图
hold on;
plot5=stairs(0:1:k,u_k0_history(:,2),'b'); %画图
hold on;
plot6=stairs(0:1:k,u_k0_history(:,3),'k'); %画图
hold on;
legend([plot4,plot5,plot6],'控制量u1','控制量u2','控制量u3');
grid on;
pause(0.01);% 时间间隔一下，防止画图太快了，感受不到控制的动态过程
end
3 控制效果
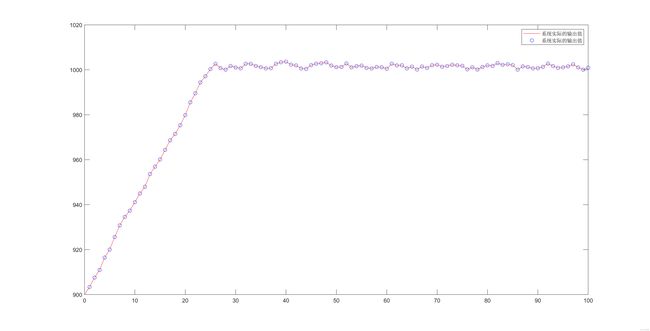
3.1 第一版本控制效果
3.2 第三版本控制效果
如有错误，请多指正，希望与大家多多交流！
错误1：比较法得到J最小值的逻辑有错误。错误已更正