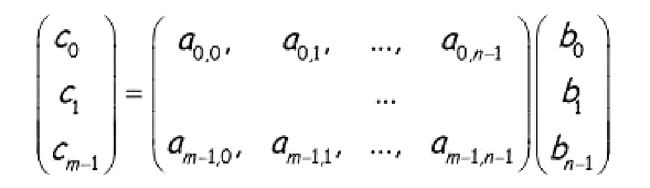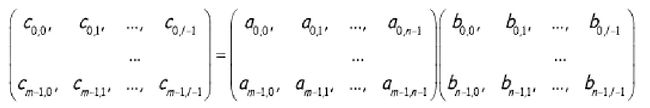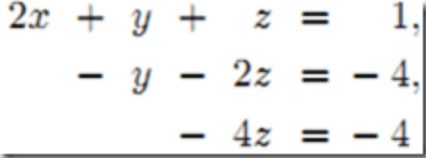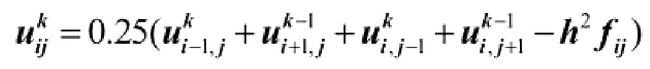常见的并行方法

目录

并行计算通常用来处理矩阵计算、线性系统（线性方程求解）、偏微分方程的相关问题。这篇文章将会介绍利用并行计算的方法是如何解决上述问题的。

1、并行方法------矩阵与向量的相乘运算

所谓矩阵与向量的相乘运算就是解决形如下面这样的问题：

这类问题的主要矛盾就是我们如何划分矩阵$A$和向量$b$，让二者的对应元素进行计算，然后合并和计算结果，得到最终的结果。

1.1、Rowwise Block-striped

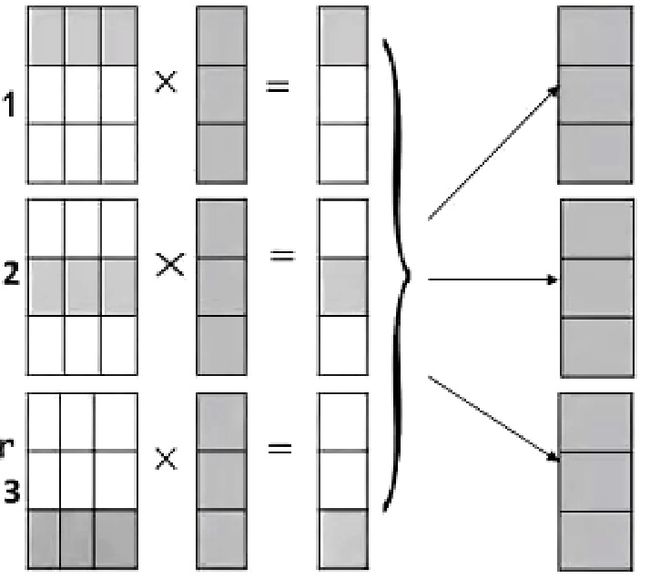
那么第一种方式就是将向量$b$拷贝到所有的节点。将矩阵$A$以行为单位分配到不同的计算节点，与向量$b$的全部元素进行计算之后，算出结果向量$c$的不同部分，然后将所有结果合并到一起。这种被称作矩阵$A$的行条带化切分。

这个方式的详细过程如上图所示，$A$的每一行分别和$b$的全部元素做计算，因为针对$A$中每一行元素的计算都是独立的，对于结果向量$c$的每一部分计算都是完全并发的，最后需要一系列的通信将计算结果组合起来。

1.2、Columnwise Block-striped

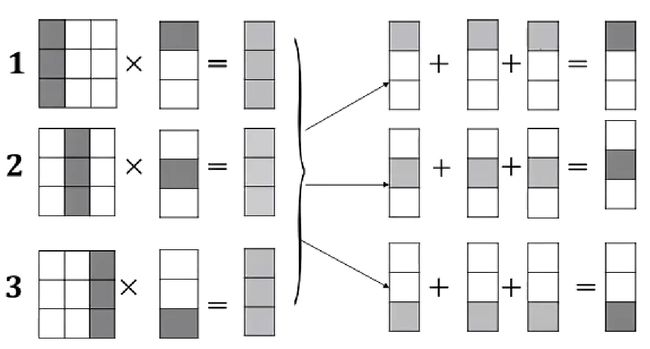
除了将$A$矩阵按行分配，我们还可以将A矩阵按列分配，这样子分配的好处是在于不用讲向量$b$的每一个元素拷贝到所有节点。每个节点只需要有向量$b$的一部分元素就好了。但是这样子进行划分，在每个节点上得到的结果就不是向量$c$的一部分，需要将所有中间结果增加，才能得到最终结果。

分开之后的计算结果的维度和向量$c$是一样的，最终需要的是将中间结果相加。

1.3、Checkerboard Block Decomposition

除了按照行与列进行条带状分配之外，还可以进行块状分布。当运算场景对应的矩阵够大的时候，以行为单位的划分方法也会导致单个计算节点的较大负载，这个时候可以采用更小的分配单元。当矩阵$A$按照块状分配之后，列向量$b$也要进行相应的截断。这样得到的结果是$c$向量每一部分的一个子集。所有我们要先将每一部分的中间结果对应相加，然后在进行组合，得到最终的向量c。

这种方法更像是前两种方法的一个组合，即在两个方向都进行条带状分配。所以对于每个节点计算结果的处理也和前两个方法类似。

2、并行方法------矩阵与矩阵的相乘运算

矩阵与矩阵的相乘运算实际上就变得复杂很多。所谓矩阵与矩阵相乘就是下面这样的操作（假设实际上都是正方形的矩阵）：

实际上对于这类问题最浅显的一套操作就是按照结果来划分任务，也就是对于结果矩阵$c$的每一位都用一个核来计算，但是这样子会带来很大的通信开销。

主流的对于矩阵相乘计算的操作主要包括下面两个。

2.1、Block- Striped Decomposition

这是一种条带状分布的划分方式。最显而易见的就是将矩阵$A$按照行来分块，矩阵$B$按照列来分块。

每一个任务得到$A$的一行，而$B$的每一列都要在任务之间传递。每个任务的每次计算都会得到矩阵的某一个元素。

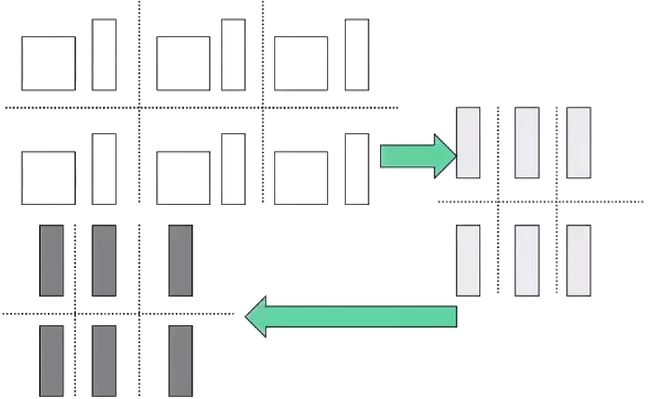
整体的计算过程如上图所示，这是一个4×4的两个矩阵相乘的例子。我们可以看到$A$矩阵的每一行是保持在任务中的，而$B$的每一列都是在任务之间循环传递的。在每次与$A$的某一行计算之后得到矩阵$C$中与$A$相同行的一位元素。这种划分方式比较符合直觉，并没有什么难的，最后在各个任务之间做一个整合，就可以得到最终的结果矩阵$C$。

还有一种比较奇怪的划分方式是将矩阵$A$与矩阵$B$都按行划分。

这种划分在每次计算的时候都可以算出矩阵一整行元素的一部分值，最终将每一部分的值相加就好了。这个方法和前文的Columnwise Block-striped方法很像。都是只能算出结果某一行的一部分，然后需要一次相加操作。整体的过程如下（这个图的第一个回合的两个任务画错了）：

以第k个任务为例，他每次做的任务就是以用矩阵$A$第$k$行的第$n$个元素分配与矩阵$B$的第$n$行的所有元素对应相乘，得到矩阵$C$第$k$行元素的一部分（所以需要不断和历史结果叠加）。

2.2、Fox’s method

这种方法将矩阵进行了分块处理，要求处理完之后全是方阵。虽然我们进行的分块，实际山矩阵分块之后的计算原则是没有变化的。和不分块的矩阵算起来没有区别：

$AB=\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\end{array}\right)\left(\begin{array}{cc}{B}_{11}& B_{12}\\ B_{21}& B_{22}\\ B_{31}& B_{32}\end{array}\right)=\left(\begin{array}{cc}{A}_{11}{B}_{11}+A_{12}{B}_{21}+A_{13}{B}_{31}& A_{11}{B}_{12}+A_{12}{B}_{22}+A_{13}{B}_{32}\\ A_{21}{B}_{11}+A_{22}{B}_{21}+A_{23}{B}_{31}& A_{21}{B}_{12}+A_{22}{B}_{22}+A_{23}{B}_{32}\end{array}\right)$

整个的计算方法非常的巧妙，要求矩阵$A$与矩阵$B$各个块的元素都要在各个任务中广播和流动。

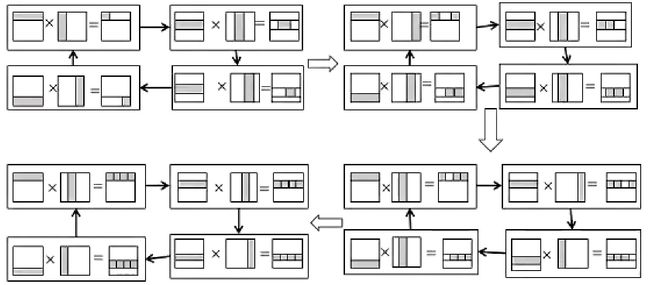
整体的算法如下面这张ppt所示：

说实话，这个算法非常巧妙，以至于每个步骤之间都有非常深刻的练习。截图中没有方块代表一个任务以及在这个任务上分配的数据。最终在每个任务中我们可以看到结果矩阵$C$对应的分块。那么对于(1,0)任务来说：

$C_{1,0}=A_{1,0}\times B_{0,0}+A_{1,1}\times B_{1,0}+A_{1,2}\times B_{2,0}+A_{1,3}\times B_{3,0}$

我们稍微改一个顺序就可以看出端倪。

$C_{1,0} = A_{1,1} × B_{1,0} + A_{1,2} × B_{2,0} + A_{1,3} × B_{3,0} + A_{1,0} × B_{0,0} $

这样子我们就可以看出端倪了。矩阵$A$横向的分块需要依次广播，矩阵$B$纵向的分块每次计算都需要挪一次位置。这样子就构成的分块矩阵的乘法。

3、并行方法------线性方程组求解

在并行方法中也可以使用高斯消元法来解线性方程组，坦率地将，线性方程组的求解问题是比较不好并行化的。关于这类问题主要采用的是高斯消元法。

高斯消元法

高斯消元法实际上非常简单，就是将线性方程组的系数矩阵转化为一个上三角矩阵，然后倒着求出所有变量的值就好。在上面的链接中讲得非常详细。

实际上，高斯消元法是一个难以完全并行的方法。我们知道高斯消元之前的方程组是这样的：

在消元之后就是这个效果：

然后我们可以通过自下而上的带入来求出每一个变量的值。而对于每一个方程的在进行消元的时候都要使用之前消元的结果。这就使得每一个方程的消元不能完全并行。但是即便如此，高斯消元法依旧使用条带状+取模的任务划分。

并且会在每个任务消元完毕之后将消元之后的结果发送给所有的任务来进行同步。最后算出每个变量的值。

4、并行方法------偏微分方程的数值解法

偏微分方程是计算领域最常解决的问题。对于一个偏微分方程来说，我们需要解决的是已知一个偏微分方程，我们需要用计算机算出微分方程的解所对应的函数在某些点对应的值。

在微分方程的数值解上，前半部分是数学的推导，计算机需要解决的是后半部分的问题。

实际上可以根据微分方程推出下面的这么一个结果：

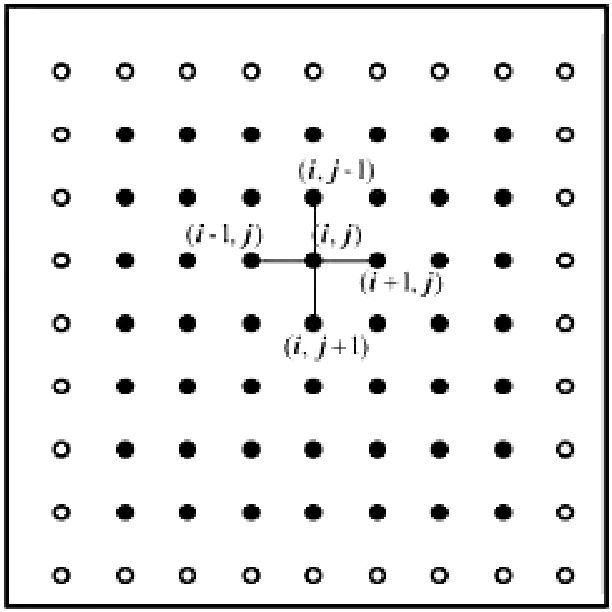
这里只是一个例子，也就是偏微分方程的解是一个函数，而这个函数在某个点的值是取决于周围其他点的值的。

而边界上的点的值是已知的，所以我们可以算出所有点的值。当然，为了保证结果的精确，这个过程要经过好多次迭代才可以。实际上这个过程叫做高斯赛德尔迭代。他的主要思路就是不断地通过一个点周围其他点在当前迭代和上一轮迭代的值来得到这个点的值。

这个思想在解线性方程组的时候也是经常遇到的：

Jacobi迭代法与Gauss-Seidel迭代法

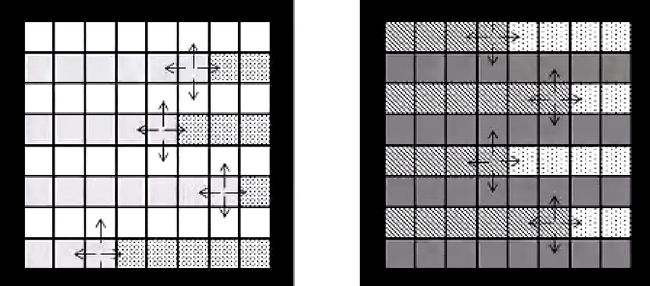
高斯赛德尔迭代在解偏微分方程时候是比较难以并行化的。首先一个点的计算需要用到周围点的值，这个过程会带来比较大的通信开销，并且在一个点的计算中分别会用到本次迭代的数据和上一次迭代的数据。比如说上面举的这个例子，对于左上的两个数据是用的是和当前数据同一次迭代的，而对于右下两个数据用的是上一次迭代的结果。

对于这类问题，任务划分的一个最简单的方式就是给每一个点都要划到一个任务里，这样子基本上只会导致这个算法最终非常低效，一个每个点的计算都需要4次通信，并且需要等待左上的两个点计算完毕才能计算。

更要命的是，高斯赛德尔迭代中有一个控制迭代是否继续执行的变量：残差。残差体现了一个一次迭代之后所有点相对上一次迭代的变化量，当这个变化量比较少了之后，我们就可以认为迭代基本上已经收敛了，可以结束迭代了。残差只保留一个最大值，对于残差的更新需要上锁，会导致算法基本上串行化。

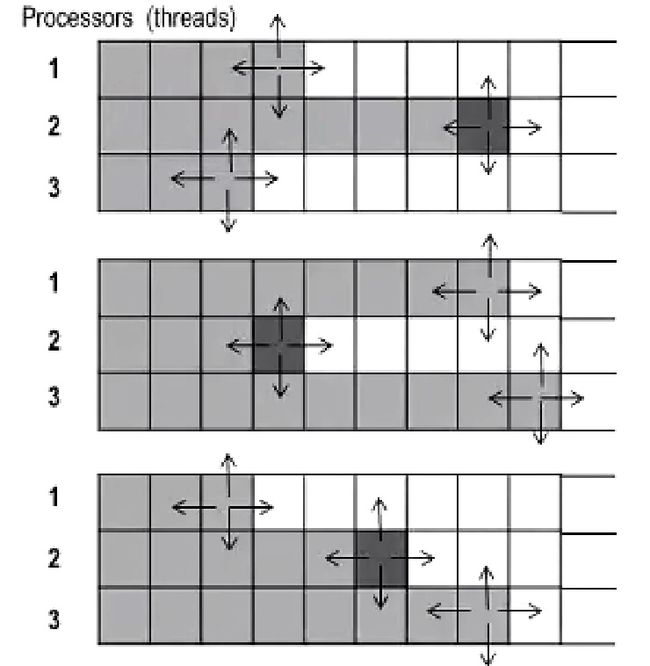
针对残差的更新导致的性能拖慢的问题，是的我们需要使用更大粒度的任务分配方式。按行划分。

这种划分方式减少了一定的通信开销，同一行的元素就不需要通信了，并且可以先针对每一行更新自己的残差，然后在这一行算法的时候再更新全局的残差。

如上图所示，这样的方式也有一定的问题，那就是每个线程的进度是不一样的，并不能保证一个节点左上的数据已经算完了。所以说这种迭代方式并不完全是高斯赛德尔迭代，会影响收敛速度。

所以说我们可以适当地上锁，来保证迭代过程尽可能是高斯赛德尔迭代。但是上锁也会导致比较严重的问题，那就是效率非常差，每一行的计算都要等到上一行基本上计算完毕之后再进行计算。

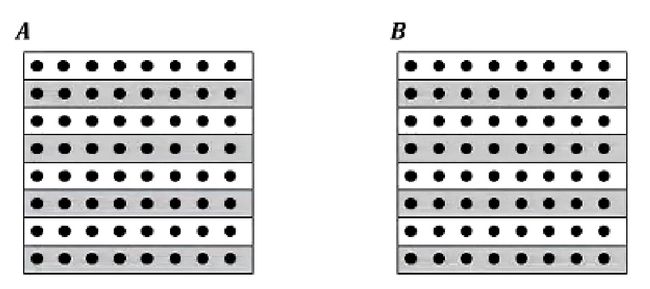
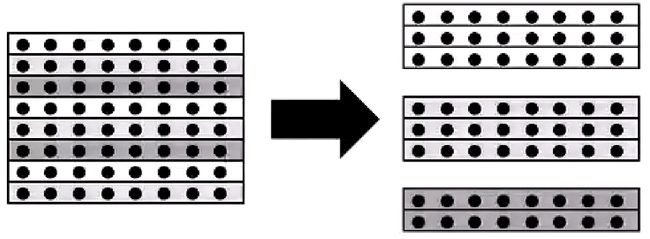
将奇数行和偶数行分开计算就是在理论与工程上比较平衡的算法。

他将矩阵分为红黑行，先同时进行奇数行，然后再进行偶数行，这样子对于偶数行来说就相对友好一些，在这个例子中偶数行对于左上两个节点的获取就是当次迭代的。所以说这也是比较推荐的算法。

除了红黑行之外，一种叫做高斯雅各比的迭代方式也可以解决类似的问题。上锁其中一个动机就是要方式有些行算得太快，使得无法获得这一行上次迭代的值了，所以高斯雅各比迭代方式就是在申请一个和当前矩阵一样大的矩阵来存储这次迭代的结果，这样子算得比较快的行并不会立即更新自己的值，这样子就可以保证取到上次迭代的值了。这种方法需要额外的空间。

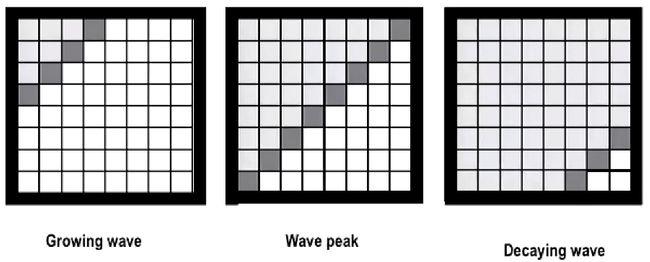
除了条带状的任务分配之外，还有一种叫做Parallel Wave的算法，这是一种“斜着算”的方式，

在这个例子中，每个点都依赖于当前迭代的左上两个点的值，那么每次就可以针对对角线元素进行并行计算。这种算法并行度不太稳定，一开始和结束比较低，在中间的时候并行度比较高。这种算法在并行效率上面会有一些损失。另外这种算法的计算结果可以和串行的高斯赛德尔迭代完全一致，因为整个的计算过程是原汁原味的高斯赛德尔迭代。

Parallel Wave这种方式有点不好的地方就是cache的利用不好，这种访问的方式局部性交叉，会导致cache的命中率下降。

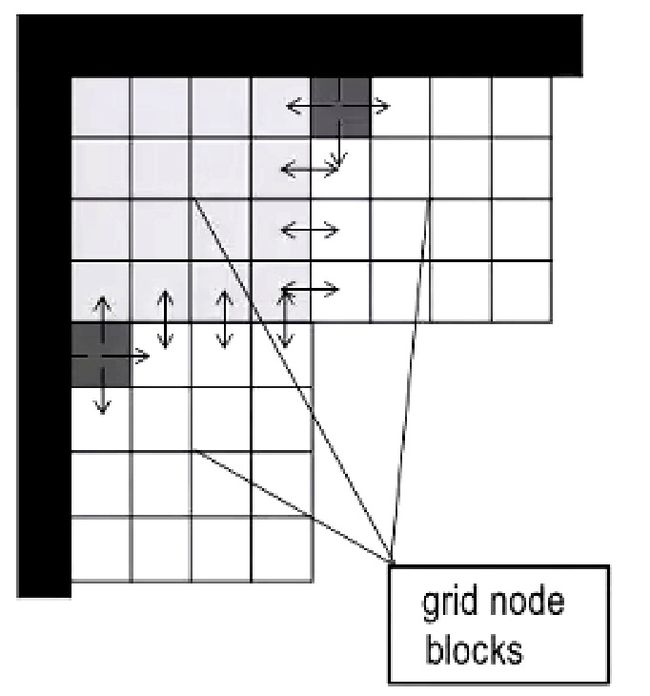
所以Parallel Wave有一个改进的版本，就是为每个任务分配更大的块，就像下图这样：

这种方式的好处就是对于每个任务来说，要进行计算的数据都比较居中，有利于Cache的命中。并且在块的交界处产生通信