机器学习笔记(六)分类评价指标、混淆矩阵、精准率、召回率、P-R曲线、ROC曲线
目录
- 1、准确率(accuracy)的陷阱
- 2、混淆矩阵(Confusion Matrix)
- 3、分类评价指标
- 4、P-R曲线
- 5、ROC曲线
1、准确率(accuracy)的陷阱
准确率:所有的预测都正确的比例。
正确率=正确数除以总数乘以百分之百。
准确率是分类算法中最基本也是最简单的评价指标,假设有一个算法,其预测某种癌症的准确率为99.9%。这个算法好吗?
99.9%的准确率看上去很高,但是如果这种癌症本身的发病率只有0.1%,即使不训练模型而直接预测所有人都是健康人,这样的预测的准确率也能达到99.9%。 更极端的情况,如果这种癌症本身的发病率只有0.01%,这算法预测的准确率还不如直接预测所有人都健康。 对于极度偏斜的数据(癌症患者的人数和健康人数量差别特别大)(skewed data),用准确率评价分类算法好坏有局限性。 解决方法:混淆矩阵
2、混淆矩阵(Confusion Matrix)
以二分类为例,0表示负例Negative,1表示正例Positive。一般正例是我们关注的部分。混淆矩阵表示如下图所示,其中:
TN:True Negative 数据样本标签是0并且模型预测值也为0的样本个数,即真正例,表示预测为真,实际也为真
FP:False Positive 数据样本标签是0而模型预测值却是1的样本个数,即假正例,表示预测为真,实际为假
FN:False Negative 数据样本标签是1而模型预测值却是0的样本个数,即假负例,表示预测为假,实际为真
TP:True Positive 数据样本标签是1并且模型预测值也为1的样本个数,即正负例,表示标签为负,实际为负

举个栗子:10000个癌症病人数据的混淆矩阵

00位置代表有9978人真实没患癌症; 模型预测9978人也没患癌症
01位置代表有12人没患癌症; 模型却预测12人患了癌症
11位置代表有2人患了癌症; 模型却预测2人没患癌症
12位置代表有8人患了癌症; 模型预测8人患了癌症
使用混淆矩阵的好处
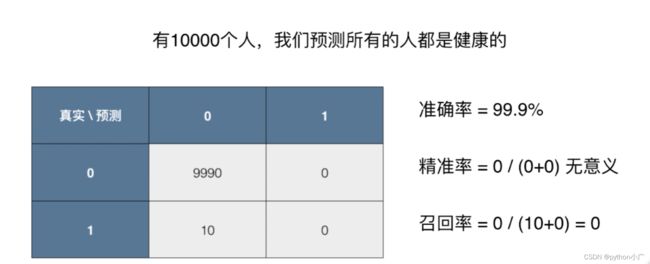
如果某种癌症的发病率为0.1%,那么预测所有人都健康的模型,虽然准确率达到99.9%。但精准率为 0 / ( 0 + 0 ) 0/(0+0) 0/(0+0) 没有意义,召回率为0,可见这个模型是个无效的模型。
3、分类评价指标
- 准确率(accuracy)
所有的预测都正确的比例
a c c u r a c y = T P + F N T P + F P + T N + F N accuracy=\frac{TP+FN}{TP+FP+TN+FN} accuracy=TP+FP+TN+FNTP+FN
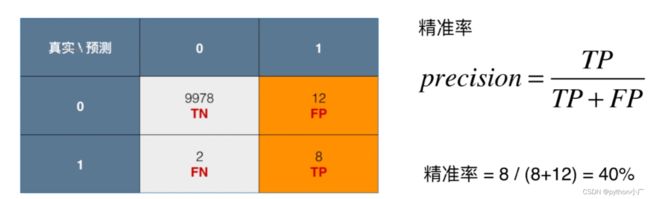
- 精确率(precision)
表示被分为正例的示例中实际为正例的比例,1是我们关注的部分
p r e c i s i o n = T P T P + F P precision=\frac{TP}{TP+FP} precision=TP+FPTP
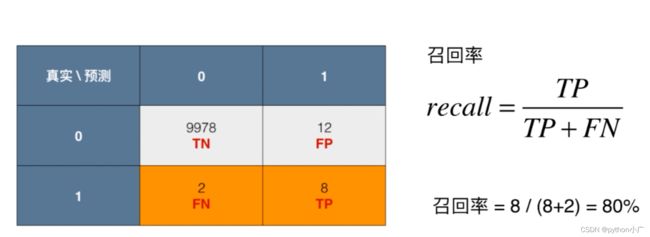
- 召回率(recall)
召回率是覆盖面的度量,度量有多个正例被分为正例
r e c a l l = T P T P + F N recall=\frac{TP}{TP+FN} recall=TP+FNTP
- F1-score
F1 Score是precision和recall的调和平均值
F 1 = 2 ⋅ p r e c i s i o n ⋅ r e c a l l p r e c i s i o n + r e c a l l F1=\frac{2\cdot precision\cdot recall}{precision+recall} F1=precision+recall2⋅precision⋅recall
4、P-R曲线
- 精准率和召回率平衡
对于逻辑回归的决策边界 θ T ⋅ x b = 0 \theta^T\cdot x_b=0 θT⋅xb=0,在 > 0 >0 >0的 一侧分类为1,在 < 0 <0 <0 另一侧分类为0。我们可以将决策边界设置为任意常量,决策边界如下: θ T ⋅ x b = t h r e s h o l d \theta^T\cdot x_b=threshold θT⋅xb=threshold,此时 > t h r e s h o l d >threshold >threshold的 一侧分类为1,在 < t h r e s h o l d

上图可以看出精准率和召回率是相互牵制、相互矛盾的,精准率增大,则召回率减小,相对的召回率增大,精准率则减小。
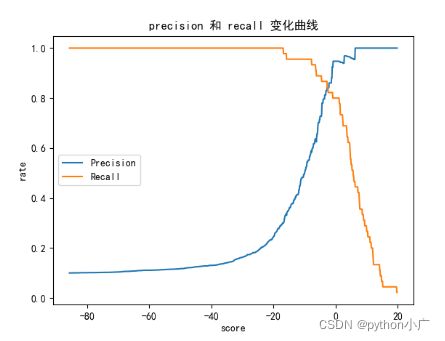
P-R曲线就是将横纵表示精确率,纵轴表示召回率。下图中我们可以随着精准率逐渐增大,召回率则逐渐减小,相对的召回率逐渐增大,精准率逐渐则减小。在这条曲线上,通常我们看见非常陡峭的突然下降的点(红点),在红点左边召回率缓缓的下降,而右边则急剧下降,这形态则告诉我们,这个急剧下降开始的位置可能就是精准率和召回率相较而言最好的平衡位置。

我们可以看见P-R曲线整体是如下图所示的曲线。召回率整体的趋势是随着精准率逐渐增大,则逐渐降低。

假设我们有两个算法,或者对同一个算法我们用两组不同的超参数训练,每训练一个模型既可以对应一个P-R曲线

我们可以看出第二组超参数的得到的曲线,整体都在第一组超参数的得到的曲线外面。这样我们既可以得出第二组超参数的得到的模型优于第一组超参数的得到的模型,道理很简单,第二组超参数的得到的曲线上的每一个点的precision和recall值都大于第一组超参数的得到的曲线上precision和recall值。如果我们有一个模型它的P-R曲线更靠外的话,模型就更加好,因此P-R曲线也可以作为选择模型、选择超参数的一个指标。对一个这个指标我们说里外可能相对抽象,更多时候,我们会用这个P-R曲线和X轴、Y轴这两个轴围成的面积来评价模型好坏,相应的面积越大,模型相应越好。
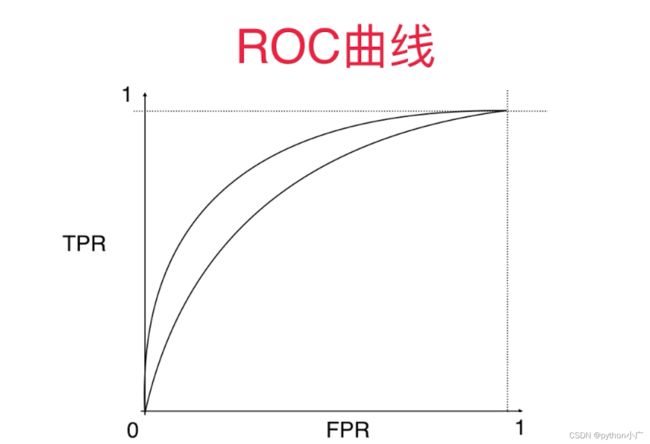
5、ROC曲线
POC 曲线:它全称为Receiver Operatioan Characteristic Curve,它描述的 TPR 和 FPR 之间的关系。
- TPR
在所有实际为正例的样本中,被正确地判断为正例之比率。
T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP

- FPR
在所有实际为负例的样本中,被错误地判断为负例之比率。
F P R = F P F P + T N FPR=\frac{FP}{FP+TN} FPR=FP+TNFP

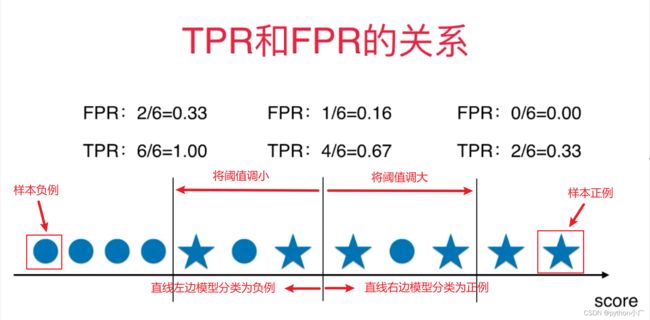
- TPR和FPR的关系
下图可以看出TPR和FPR之间是一个相一致的,TPR越大,FPR也越大,TPR越小,FPR也就越小
- ROC曲线
我们以FPR为横轴,TPR为纵轴,得到如下ROC空间:
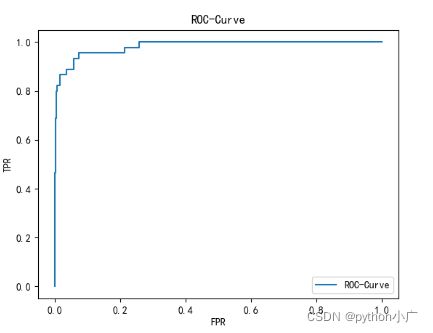
对于ROC曲线通常关注的是这条曲线下面的面积的大小。这条曲线下面面积(AUC)越大,对应我们训练的模型分类效果越好。所以ROC曲线下面的面积可以作为一个分类指标,叫做AUC(Area Under Curve)。对于这面积它最大值为1,最小值为0。因为对于这条曲线而言,它的定义域和值域都在 [ 0 , 1 ] [0, 1] [0,1]之间的,因此AUC的取值范围也在 [ 0 , 1 ] [0, 1] [0,1]之间。