五种傅里叶变换的分析（FT、FS、DTFT、DFT、DFS）（基于MATLAB）

五种傅里叶变换

FT： 傅里叶变换 Fourier Transform
FS： 傅里叶级数 Fourier Series
DTFT：离散时间傅里叶变换 Discrete-time Fourier Transform
DFT： 离散傅里叶变换 Discrete Fourier Transform
DFS： 离散傅里叶级数 Discrete Fourier Series

各种信号时域和频域的关系

时域	频域
连续 、非周期性	非周期性、连续
连续 、周期性	非周期性、离散
离散 、非周期性	周期性、连续
离散 、周期性	周期性、离散

先放一张图让大家理解一下这几种变换相互之间的联系与区别。

在这篇文章中，我会用MATLAB画图的方式来解释这五种傅里叶变换的区别与联系。

一、（FT）傅里叶变换

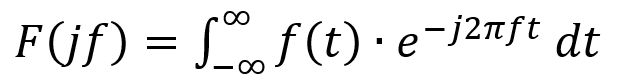
这是傅里叶变换的公式，它可以将一个 以时间t为自变量 的连续的信号 f(t) 转换为 以频率为自变量 的函数 F(jf)，该函数是复数形式的。

该公式有三个关键点：

• f(t) 是一个时域上连续的信号。
• t 从负无穷到正无穷积分。
• 频率f 连续，其得到的结果 F(jf) 也为频率域上连续的频谱。

但计算机并不能处理连续的信号，得到的结果也是离散的，而且计算机只能处理有限长度的数据。故计算机不能实现傅里叶变换。

大家都知道一个连续的函数之所以连续，是因为其中每个值之间的间隔为无穷小，离散的信号不管间距多么的小，始终只能无限接近于连续的信号。
那么我们给与这样一个假设：
当离散的间隔达到一个非常小的程度，我们就将该离散信号看成是连续信号。
① 将信号f(t)以∆t=0.001s进行采样，由于采样间隔很小，近似看成时域上连续的信号。
② 频率f也取一个∆f=0.001Hz的间隔，由于频率间隔很小，近似看成频率域上连续。

这样我们就可以通过计算机实现傅里叶变换了。

1、

我们产生出一个连续的信号（以0.001s为采样间隔），如下：


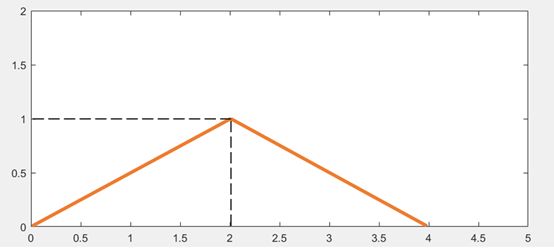
MATLAB代码：

Dt = 0.001;   %信号采样间隔，s
tlen = 4;     %信号长度，s
t = 0:Dt:tlen;
tsize = tlen/Dt+1;
k = 1;
for i=t
    if i<=2
        y(k) = 0.5*i;
    end
    if i>2
        y(k) = 2-0.5*i;
    end
    k=k+1;
end
plot(t,y);

这里产生了一个三角形状的信号，只有在t=0~4s有值，其余时刻都为0，这样便可以使得傅里叶变换在负无穷到正无穷上积分有意义。

2、

进行傅里叶变换：

MATLAB代码：

f = -3:0.001:3;     %频率的分辨率0.001Hz，近似代表连续的频谱
num = size(f);
num = num(2);       %保存横坐标频率的个数
ff = 0*ones(1,num); %用来保存计算得到的个频率下的结果
 
counts = 1;
for k1=f
    for k2=1:1:tsize
        ff(counts) = ff(counts)+Dt*y(k2)*exp(-2*pi*1i*k1*t(k2));
    end
    counts=counts+1;
end

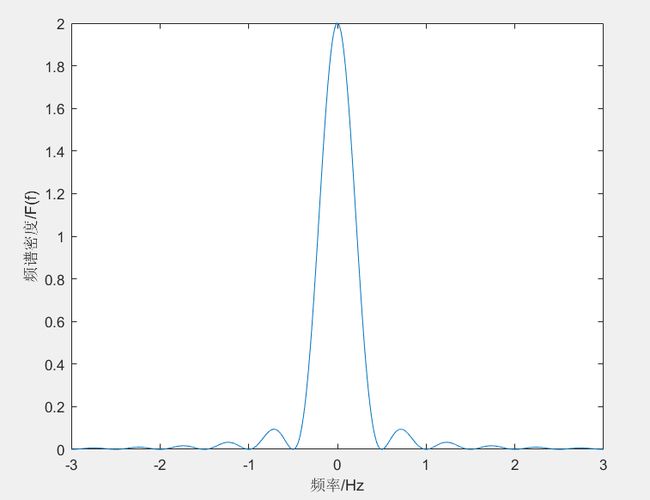
plot(f,abs(ff));
xlabel('频率/Hz');
ylabel('频谱密度/F(f)');

该信号为连续信号，变换后的频谱也为连续谱，其纵坐标的值代表频谱密度，并不是真实信号中所含频率成分的幅值的大小。

我们得到一个结论：信号是连续、非周期的，其频谱是非周期、连续的。

二、（FS）傅里叶级数

傅里叶级数是对周期信号进行频谱展开，故只有周期信号才有傅里叶级数。

1、

对原信号进行周期延拓，变为周期为原信号时间长度 T 的周期信号：

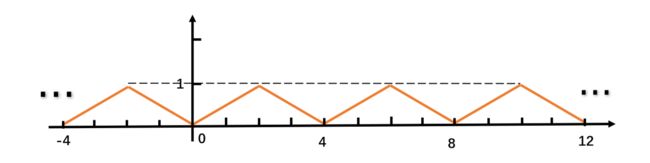
然后对延拓后的信号进行傅里叶级数展开，周期为 T=4s，基频为 f0=1/4 Hz：
傅里叶级数公式：

tlen = 4;
f = -3:1/tlen:3;   %频率的间隔0.25Hz
num = size(f);
num = num(2);     %保存横坐标频率的个数
ff = 0*ones(1,num);  %用来保存计算得到的个频率下的结果
counts = 1;
for k1=f
    for k2=1:1:tsize
        ff(counts) = ff(counts)+1/tlen*Dt*y(k2)*exp(-2*pi*1i*k1*t(k2));
    end
    counts=counts+1;
end
stem(f,abs(ff));
xlabel('频率/Hz');
ylabel('频率幅值/F(f)');

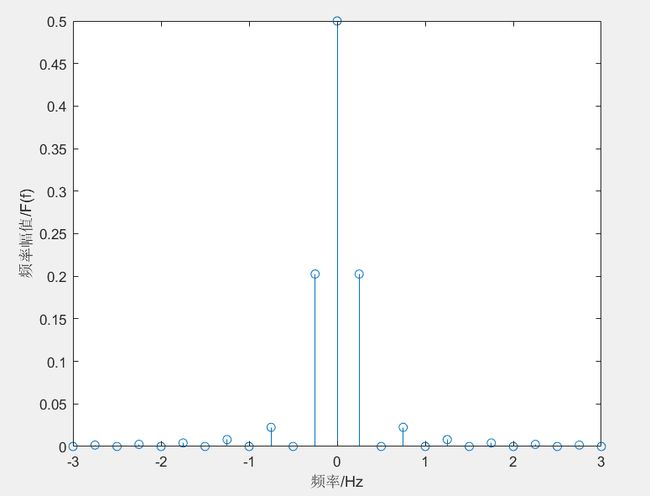
该频谱为离散频谱，以 f0=1/4Hz 为基频，求得的离散双边频谱。

我们得到一个结论：信号是连续、周期的，其频谱是非周期、离散的。

相当于对原来的频谱密度函数进行等间距采样，然后缩减为1/4倍。

原理很简单：
周期延拓相当于原信号与一个梳状函数（单位冲激序列）进行了卷积，而梳状函数的频谱也是一个冲激序列，只不过幅值和周期发生了改变，时域的卷积相当于频域的乘积，所以得到的频谱就是原频谱进行了等间距采样。

放图

三、（DTFT）离散时间傅里叶变换

以上我们遇到的信号都是时域连续的信号，我们都是使用间隔很小的采样来近似连续信号（尽管之前是将信号用非常小的间隔进行划分，相当于间隔无穷小，来近似看成连续的信号，但仍然不是连续的信号）。
这样我们便要对信号真正地进行离散时间采样，采样频率为Fs。
我们假设采样频率为 Fs=200Hz ，得到如下的一个离散的序列 x(n)。

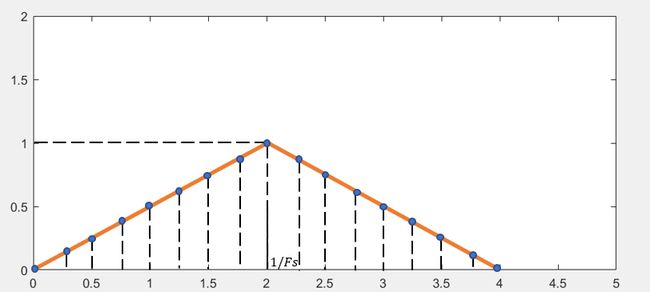
这样就将信号在时域上离散化了。
引出离散时间傅里叶变换公式：
得到频谱图，如下（截取了其中一个段）：

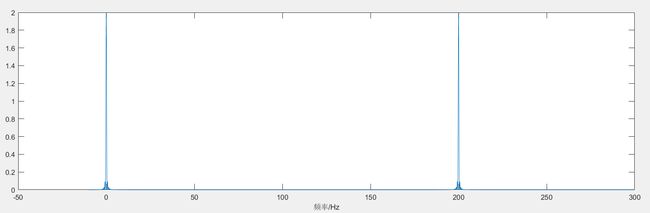
可以看到，得到的仍然是一个连续的频谱（f没有离散化）。但是该连续的频谱变为周期性的了，且周期和采样频率有关，周期 Tf=Fs=200Hz。

我们得到一个结论：信号是离散、非周期的，其频谱是周期、连续的。

四、（DFT）离散傅里叶变换

对该连续的频谱，计算机也要对频率进行离散采样，即频率离散化，因为其频谱是周期的，故只在一个周期 Tf 内进行采样计算即可。
频谱周期为Tf，其中只取一个周期计算，将Tf分成N份。
理论上一个周期内分为多少份都可以，只要得到的频谱能够清楚地反应其变化规律，不失真就行。但要做到这一点，其分成的份数是比较多的。
一般取 N 等于原信号离散采样的个数，N=信号长度tlen*采样频率Fs，故频率采样间隔Tf/N=Tf/(tlen*Fs)=1/tlen Hz。
将信号中值为0的部分去掉，信号变为一个有限长的序列x(n)，长度为N。

得到的频谱成为离散傅里叶变换公式：

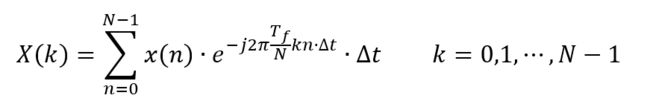
其中，Tf=Fs=1/∆t，上式化简为：

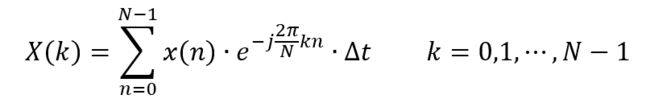
其中 ∆t 不过是一个常数，不影响频谱的相对大小，将其归一化为1：

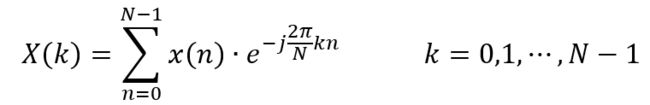
这便是 离散傅里叶变换（DFT） 的表达式。

下图便是离散傅里叶变换得到的频谱：

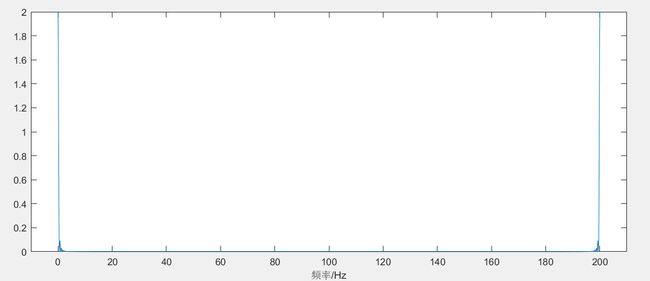
在计算机当中，这是我们最常用的傅里叶变换。
但其得到的值只能表示各频率成分幅值的相对大小，并不是信号各频率成分的真正幅值的大小。
想要得到幅值的真正大小，还要进行进一步的变化。

五、（DFS）离散傅里叶级数

在上面，我们通过周期延拓得到了一个周期性的信号，其得到的频谱是一个离散的非周期的频谱。
如果我们对该周期信号进行离散采样，其对应的频率将会进行周期延拓，变成一个离散的周期的频谱；
或者我们对先离散过后的信号进行周期延拓，其对应的频率会被离散采样，也同样变为一个离散的周期的频谱。
我们得到一个结论：信号是离散、周期的，其频谱是周期、离散的。

该公式只与离散傅里叶变换差了一个1/N，该公式得到的值便是信号中各频率成分的幅值的1/2。
1/2的原因在于此处用到的傅里叶级数是复指数形式的傅里叶级数，复指数形式的傅里叶级数与三角函数形式的傅里叶级数相差1/2。

六、如何使用离散傅里叶变换(DFT)？

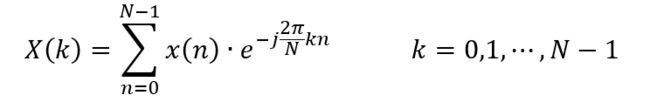
1、我们在得到一段信号后，首先得到的信息是该信号的时间长度 T。
2、以一定的采样频率 Fs 进行采样，可以得到一个离散序列x(n)，其长度为 N=T*Fs。
3、x(n)、 N代入公式，得到一个频率序列 X(k),其长度也为 N，该序列中的值为复数。

我们要做的便是对该序列X(k)，进行一定的处理，来得到不同频率的幅值大小。
4、X(k) 频率序列的频率是以 1/T 为间隔的，以此为横坐标。
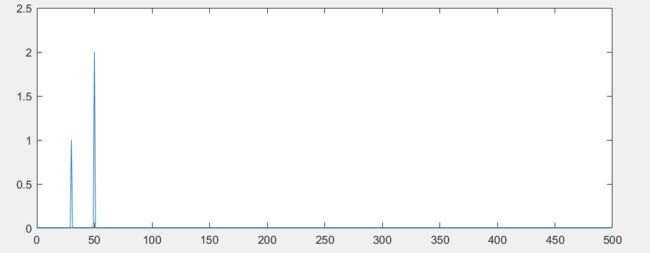
5、若将频率序列X(k)再除以N，乘以2，然后取前一半数据（因为数据是对称的，只有一半是有用的），便得到各频率所对应的正是幅值大小，以此为纵坐标。
6、画出的图，便是能够反映各频率成分幅值大小的频谱图。

下面使用MATLAB来做一个演示。
使用FFT代替DFT。

快速傅里叶变换FFT只是一种DFT的快速算法，两者得到的结果是完全相同的。

1、得到信号序列。

%定义采样频率、采样点数等
Fs = 1000;          %采样频率
Dt = 1/Fs;          %采样周期
n = 1000;           %采样点数
T = N*Dt;           %采样信号的时间长度
t = (0:(N-1))*Dt;  %离散时间点，以Fs为采样频率

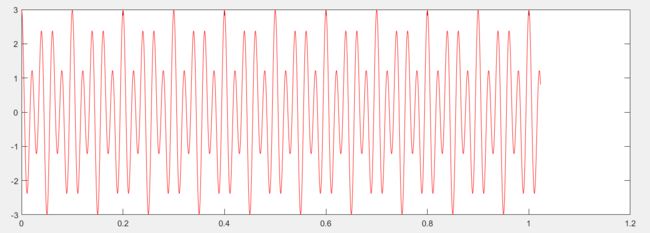
y = 2*cos(2*pi*50*t)+cos(2*pi*30*t); 
%画出时域图
plot(t,y,'r');
xlabel('Time');
ylabel('幅值');
title('时域信号')

2、对序列进行FFT快速傅里叶变换。

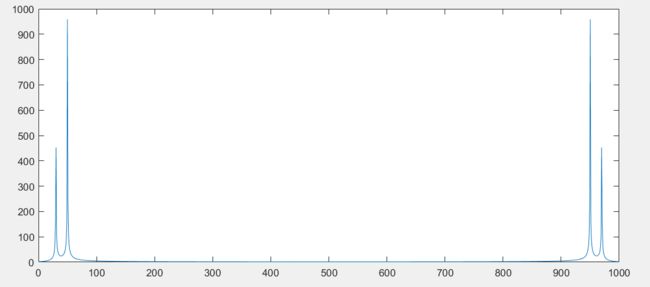
Y = fft(y);     %快速傅里叶变换
f = 0:1/T:Fs;
f = f(1:end-1);   %去掉最后一个频率点
plot(f,abs(Y));

3、处理。

mag = 2*abs(Y)/N;          %除以N，乘以2。
plot(f(1:N/2),mag(1:N/2)); %取一半数据显示

谢谢观看，希望对各位有所帮助！