SiamFC论文学习笔记
SiamFC论文学习笔记
- 引言
- 相似度学习
- 网络结构
- 损失函数的定义
- 优化与训练方案
- 总结
引言
这是我写下的第一篇博文,主要目的是提升学习自己的主动性,对自己学到的知识进行及时总结反思,也便于在后续回顾时起到温故而知新的效果。读研小白一枚,博文不管是知识面还是写作风格上都有很多漏洞,欢迎大家及时指出,共同交流学习和进步。另外,想请教一下大家平时阅读论文和学习代码时采用什么样的方法或者步骤,自觉总是不得要领,学习效率比较低。
论文:《Full-Convolutional Siamese Networks for Object Tracking》
在本篇论文中,作者提出了全卷积孪生网络(Full-Convolutional Siamese Network,简称SiamFC)。这一网络提出的主要目的是解决如何追踪视频中的任意目标的问题。孪生网络的思想在本篇论文之前其实已经被提出过,但是该论文第一次引入了互相关层(correlation layer)作为两个分支的融合张量(fusion tensor),大大提高了跟踪精度。
相似度学习
对于任意给定的一个目标,要解决目标跟踪问题,孪生全卷积网络提出的主要思路是相似度学习。通俗地说,就是给定尺寸相同的模板图z和样本图x,我们用网络学习一个评价函数f(x,z) ,对两幅图的相似度进行打分,相似度越大,样本图就越可能包含给定模板图中的目标物体。
相似度学习这一思路应用在目标跟踪问题中,就是把上一帧中的目标物体图像作为模板,在本帧中选取多个相同尺寸的候选图,分别进行相似度计算,选出其中评价函数给分最高的候选图,其所在位置就是本帧中目标物体的位置。在原论文中,视频第一帧的目标物体图像被设置为最初的模板图。
网络结构
孪生全卷积网络的总体结构如图所示。
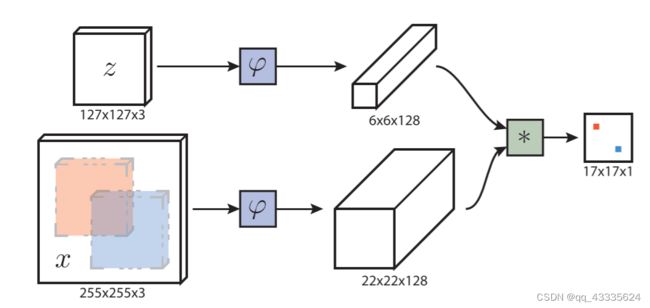
顾名思义,孪生网络是由两个结构相似的网络组成的。z为模板图,x为输入的样本图。两个 φ \varphi φ 表示两个特征提取网络,即原文中所说的embedding(用于降维的嵌入网络),论文中采用的是经典的AlexNet。 ∗ \ast ∗ 表示互相关操作: f ( z , x ) = φ ( z ) ⋆ φ ( x ) + b I I f(z,x)=\varphi(z)\star\varphi(x)+bII f(z,x)=φ(z)⋆φ(x)+bII
⋆ \star ⋆即我们平常熟悉的卷积操作,bII是每个子窗口对应的值,一个偏移量矩阵,看其他大佬解读似乎是通过什么窗口惩罚操作来获取的,这里还是需要继续阅读源码。
因此,整个孪生网络的流程如下,以论文输入尺寸的图像为例,127×127×3的模板图z(上一帧的目标物体图)和255×255×3的样本图x分别经过特征提取之后,再进行卷积(互相关操作),可得到一个分数图(分数矩阵),存储相似度评价的结果。
这里我一开始很疑惑,前文不是要求模板图z和样本图x尺寸相同吗?文章中提到,相似度最初的思路是在本帧图像中选取多个与模板图z尺寸相同的候选图x(子窗口),这样一来,经过如图的流程,最后得到的分数就会是一个数值,而非一个矩阵。但是这样一来就要对每个候选图(子窗口)都要执行一次同样的操作,而本结构则是用一副更大的搜索图取代一个子窗口候选图,最后得到的分数图各元素实际上就是模板图与搜索图中各个子窗口的相似度评价结果,相当于一次对多个子窗口打分,这样大大减少了时间成本。
再说说搜索图的选取,在跟踪过程中,是根据上一帧搜索到的目标图像的中心位置在本帧图中生成255×255×3的搜索图作为输入的x。经过孪生网络得到分数图后,用最大得分所在位置与分数图中心位置之差(即相对位置)乘以孪生网络的步幅(即从输入图像到输出特征图的缩放倍数),即可得出目标从一帧到下一帧的位移。通过缩放模板图像,在一个正向传播中可搜索多种缩放比例。(这一段在原文中不太懂)
损失函数的定义
网络的损失函数采用logistic损失函数,损失函数基于孪生网络输出的分数图进行定义。
对单一分数的损失函数定义如下:
l ( y , v ) = l o g ( 1 + e x p ( − y v ) ) l(y,v)=log(1+exp(-yv)) l(y,v)=log(1+exp(−yv))
其中v是模板图与某一个子窗口的相似度评价分数,y ∈ \in ∈{1,-1}是对应的标签值(具体在后面解释)。
如果把分数图的位置集合定义为D,其中的每个位置记为u,每个u实际上代表输入的搜索图x中的一个子窗口。由上面的损失函数可以继续定义分数图的损失函数:
L = 1 ∣ D ∣ ∑ u ∈ D l ( y [ u ] , v [ u ] ) L=\frac{1}{|D|}\sum_{u\in D}l(y[u],v[u]) L=∣D∣1u∈D∑l(y[u],v[u])
可以发现,这一损失函数是基于均值的思想定义的。
最后说说每个子窗口u的标签值y的定义:
y [ u ] = { + 1 k ∣ ∣ u − c ∣ ∣ ≤ R − 1 o t h e r w i s e y[u]=\left\{\begin{matrix} +1&k||u-c||\le R \\ -1&otherwise \end{matrix}\right. y[u]={+1−1k∣∣u−c∣∣≤Rotherwise
这里人为定义了一个范围半径R,对于分数图中那些与中心点c的距离 ∣ ∣ u − c ∣ ∣ ||u-c|| ∣∣u−c∣∣再乘以网络的步幅k小于等于R的元素u,记为正例,实际上就是在搜索图中与搜索图中心点距离小于R的那些子窗口。
为了平衡正负例数量的不均衡,还要对正例和负例对应的损失函数加权处理。
优化与训练方案
有了损失函数,就可以确定优化训练方案了。本论文采用深度学习经典的学习方式——随机梯度下降法(SGD)进行孪生网络参数 θ \theta θ的学习。
结合网络损失函数的定义,整个问题就可以转换为使用SGD方法求解
a r g min θ E ( y , z , x ) [ L ( y , f ( z , x ; θ ) ) ] arg \min_{\theta} E_{(y,z,x)} [L(y,f(z,x;\theta))] argθminE(y,z,x)[L(y,f(z,x;θ))]
总结
本论文的主要知识暂时总结到这里,不足的部分欢迎大家批评指正。论文阅读过程中参考了许多大佬的博文分析,非常感谢。
推荐一篇分析得很不错的博文:
SiamFC 学习(论文、总结与分析)