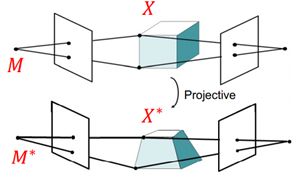
【三维重建】三维重建学习笔记（5）—— 双目立体视觉系统

第五章 双目立体视觉系统

一、平行视图

1. 基础矩阵的另一种形式

        之前定义了基础矩阵\(F={{{K}'}^{-T}}[{{T}_{\times }}]R{{K}^{-1}}\)

极几何

        不妨设世界坐标系和\({{O}_{1}}\)摄像机坐标系重合，\({e}'\)可以看成是\({{O}_{1}}\)在第二个像平面上投影的结果。因此可以得到：\[{e}'={K}'\left[ \begin{matrix}   R & T  \\\end{matrix} \right]\left[ \begin{matrix}   0  \\   0  \\   0  \\   1  \\\end{matrix} \right]={K}'T\]

        另外，数学上有叉乘性质：对于任何向量\(t\)，如果\(M\)可逆，相差一个尺度的情况下：

\[\left[ {{t}_{\times }} \right]M={{M}^{-T}}\left[ {{({{M}^{-1}}t)}_{\times }} \right]\]

        令\(t=T,M={{{K}'}^{-1}}\)，则\(\left[ {{T}_{\times }} \right]{{{K}'}^{-1}}={{{K}'}^{T}}\left[ {{({K}'T)}_{\times }} \right]\)，即\(\left[ {{T}_{\times }} \right]={{{K}'}^{T}}\left[ {{({K}'T)}_{\times }} \right]{K}'\)

        因此\(F={{{K}'}^{-T}}[{{T}_{\times }}]R{{K}^{-1}}={{{K}'}^{-T}}{{{K}'}^{T}}\left[ {{({K}'T)}_{\times }} \right]{K}'R{{K}^{-1}}=\left[ {{({K}'T)}_{\times }} \right]{K}'R{{K}^{-1}}=\left[ {{{{e}'}}_{\times }} \right]{K}'R{{K}^{-1}}\)

        由此，基础矩阵的另一种形式如下：\[F=\left[ {{{{e}'}}_{\times }} \right]{K}'R{{K}^{-1}}\]

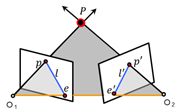
2. 极几何特例：平行视图

平行视图

         不妨设\(K={K}'\)，\(R=I\)，\(T=\left[ \begin{matrix}   T  \\   0  \\   0  \\\end{matrix} \right]\)，\({e}'=\left[ \begin{matrix}   1  \\   0  \\   0  \\\end{matrix} \right]\)，

        则\(F=\left[ {{{{e}'}}_{\times }} \right]{K}'R{{K}^{-1}}=\left[ \begin{matrix}   0 & 0 & 0  \\   0 & 0 & -1  \\   0 & 1 & 0  \\\end{matrix} \right]\)

        极线\(l={{F}^{T}}{p}'=\left[ \begin{matrix}   0 & 0 & 0  \\   0 & 0 & 1  \\   0 & -1 & 0  \\\end{matrix} \right]\left[ \begin{matrix}   {{{{p}'}}_{u}}  \\   {{{{p}'}}_{v}}  \\   1  \\\end{matrix} \right]=\left[ \begin{matrix}   0  \\   1  \\   -{{{{p}'}}_{v}}  \\\end{matrix} \right]\)

        \({{{p}'}^{T}}Fp=0\Rightarrow \left[ \begin{matrix}   {{{{p}'}}_{u}} & {{{{p}'}}_{v}} & 1  \\\end{matrix} \right]\left[ \begin{matrix}   0 & 0 & 0  \\   0 & 0 & -1  \\   0 & 1 & 0  \\\end{matrix} \right]\left[ \begin{matrix}   u  \\   v  \\   1  \\\end{matrix} \right]=0\Rightarrow {{p}_{v}}={{{p}'}_{v}}\)

        由上面两行，极线是水平的且平行于\(u\)轴，\(p\)和\({p}'\)的\(v\)坐标一样。因此\({p}'\)点沿着扫描线寻找即可。

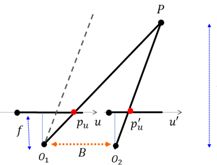
3. 平行视图的三角测量

平行视图模型的俯视图

        由相似关系可得：\[{{p}_{u}}-{{{p}'}_{u}}=\frac{Bf}{z}\]

        定义视差为\({{p}_{u}}-{{{p}'}_{u}}\)，则可以很容易地从视差得到深度信息，且视差与深度\(z\)成反比。

视差图与深度图

注意：

        由于遮挡现象的存在，因此部分点的深度信息是无法获取的，在深度图中对应黑色像素部分。

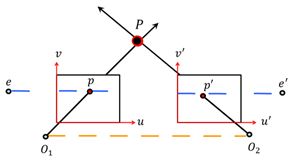
二、图像校正

1. 校正目标

        求解\(H\)和\({H}'\)使得变换后的图像的与基线平行的平面共面，且极线平行于\(u\)轴。

图像校正

2. 图像校正的步骤

        1. 在两幅图像\(I\)和\({I}'\)找到一组匹配点\({{p}_{i}}\leftrightarrow {{{p}'}_{i}}\)，不少于8个。

        2. 计算基础矩阵\(F\)（八点算法等），求解两幅图像中的极点\(e\)和\({e}'\)

求解\(e\)：第一步，\({{l}_{i}}={{F}^{T}}{{{p}'}_{i}}\)；第二步，解方程\(\left[ \begin{matrix}   {{l}_{1}}  \\   \vdots   \\   {{l}_{n}}  \\\end{matrix} \right]e=0\)

求解\({e}'\)：第一步，\({{{l}'}_{i}}=F{{p}_{i}}\)；第二步，解方程\(\left[ \begin{matrix}   {{l}_{1}}{{^{\prime }}^{T}}  \\   \vdots   \\   {{l}_{n}}{{^{\prime }}^{T}}  \\\end{matrix} \right]{e}'=0\)

        3. 选择透视变换\({H}'={{T}^{-1}}GRT\)将\({e}'\)映射到无穷远点\((f,0,0)\)

\[T=\left[ \begin{matrix}   1 & 0 & -\frac{width}{2}  \\   0 & 1 & -\frac{height}{2}  \\   0 & 0 & 1  \\\end{matrix} \right]\]

变换后\({e}'\)的齐次坐标为\(({{{e}'}_{1}},{{{e}'}_{2}},1)\)

\[R=\left[ \begin{matrix}   \alpha \frac{{{{{e}'}}_{1}}}{\sqrt{{{{{e}'}}_{1}}^{2}+{{{{e}'}}_{2}}^{2}}} & \alpha \frac{{{{{e}'}}_{2}}}{\sqrt{{{{{e}'}}_{1}}^{2}+{{{{e}'}}_{2}}^{2}}} & 0  \\   -\alpha \frac{{{{{e}'}}_{2}}}{\sqrt{{{{{e}'}}_{1}}^{2}+{{{{e}'}}_{2}}^{2}}} & \alpha \frac{{{{{e}'}}_{1}}}{\sqrt{{{{{e}'}}_{1}}^{2}+{{{{e}'}}_{2}}^{2}}} & 0  \\   0 & 0 & 1  \\\end{matrix} \right]\]

\({{{e}'}_{1}}>0\)时\(\alpha =1\)，反之\(\alpha =1\)，变换后\({e}'\)的齐次坐标为\((f,0,1)\)

\[G=\left[ \begin{matrix}   1 & 0 & 0  \\   0 & 1 & 0  \\   -\frac{1}{f} & 0 & 1  \\\end{matrix} \right]\]

变换后\({e}'\)的齐次坐标为\((f,0,0)\)

        4. 寻找对应的透视变换矩阵\(H\)使得\(\sum\limits_{i}{d(H{{p}_{i}},{H}'{{{{p}'}}_{i}})}\)最小，以确保变换后的图像的与基线平行的平面共面。

        5. 分别用矩阵\(H\)和\({H}'\)，对左右两幅图像\(I\)和\({I}'\)进行重采样。

图像校正

三、对应点搜索

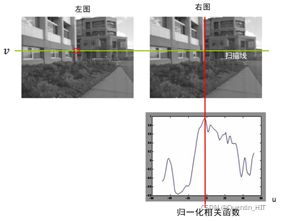
1. 相关匹配法

对应点搜索

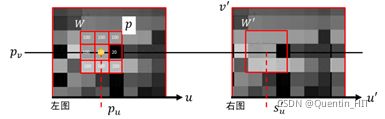
1. 在左图中\(p=({{p}_{u}},{{p}_{v}})\)处选择一个3×3（也可是5×5等）窗口\(W\)，展开成9×1向量：\[w={{\left[ \begin{matrix}   100 & 100 & 100 & 100 & 100 & 20 & 160 & 180 & 200  \\\end{matrix} \right]}^{T}}\]
2. 在右图中沿扫描线在每个位置\({{{s}'}_{u}}\)处建立窗口\({W}'\)，并获得\(w'\)向量；
3. 计算每个\({{{s}'}_{u}}\)位置\({{w}^{T}}{w}'\)的值；
4. \({{{p}'}_{u}}=\arg \underset{{{{{s}'}}_{u}}}{\mathop{\max }}\,{{w}^{T}}{w}'\)，即\({{w}^{T}}{w}'\)最大的点为\({{p}_{u}}\)所对应的\({{{p}'}_{u}}\)。

2. 归一化匹配法

        相关匹配法的问题：窗口中的像素的灰度值发生剧烈变化

1. 在左图中\(p=({{p}_{u}},{{p}_{v}})\)处选择一个3×3（也可是5×5等）窗口\(W\)，展开成9×1向量：\[w={{\left[ \begin{matrix}   100 & 100 & 100 & 100 & 100 & 20 & 160 & 180 & 200  \\\end{matrix} \right]}^{T}}\]并计算灰度均值\(\bar{w}\)；
2. 在右图中沿扫描线在每个位置\({{{s}'}_{u}}\)处建立窗口\({W}'\)，并获得\(w'\)向量，计算灰度均值\(\bar{{w}'}\)；
3. 计算每个\({{{s}'}_{u}}\)位置\(\frac{{{(w-\bar{w})}^{T}}({w}'-{\bar{w}}')}{\left\| w-\bar{w} \right\|\left\| {w}'-{\bar{w}}' \right\|}\)的值；
4. \({{{p}'}_{u}}=\arg \underset{{{{{s}'}}_{u}}}{\mathop{\max }}\,\frac{{{(w-\bar{w})}^{T}}({w}'-{\bar{w}}')}{\left\| w-\bar{w} \right\|\left\| {w}'-{\bar{w}}' \right\|}\)，即\(\frac{{{(w-\bar{w})}^{T}}({w}'-{\bar{w}}')}{\left\| w-\bar{w} \right\|\left\| {w}'-{\bar{w}}' \right\|}\)最大的点为\({{p}_{u}}\)所对应的\({{{p}'}_{u}}\)。

归一化函数示例

3. 窗口\(W\)大小的影响

窗口大小的影响

        较小的窗口细节丰富，但是有更多的噪声；

        较大的窗口视差图更平滑、噪声更小，但是会丢失细节。

4. 相关法存在的问题

        1. 透视缩短

透视缩短

         2. 遮挡问题

遮挡问题

        为了减少透视缩短和遮挡的影响，希望有更小的\(\frac{B}{z}\)比值。但是，当\(\frac{B}{z}\)小时，测量值的小误差意味着估算深度的大误差。

估算深度的大误差

         3. 同质区域

同质区域

         4. 重复模式

重复模式

5. 引入更多的约束解决对应点问题

• 唯一性约束：一张图像中的任何点，在另一张图像中最多只有一个匹配点
• 顺序约束/单调性约束：左右视图中的对应点次序一致
• 平滑性约束：视差函数通常是平滑的（除了遮挡边界）

第六章 多视图几何

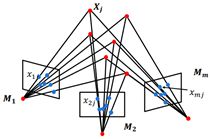
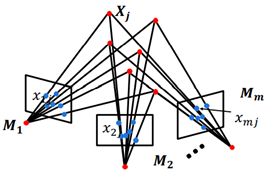
一、运动结构恢复问题（Structure From Motion）

1. 问题概述

运动结构恢复

已知：

        \(n\)个3D点\({{X}_{j}}\)在m张图像中的对应点的像素坐标\({{x}_{ij}}(i=1,...,m,j=1,...,n)\)，且\({{x}_{ij}}={{M}_{i}}{{X}_{j}}(i=1,...,m,j=1,...,n)\)。其中，\({{M}_{i}}\)为第\(i\)张图片对应的摄像机的投影矩阵。

求解：

        运动(motion)：\(m\)个摄像机的投影矩阵\({{M}_{i}}(i=1,...,m)\)；

        结构(structure)：\(n\)个三维点\({{X}_{j}}(j=1,...,n)\)的坐标。

2. 三种典型的运动恢复结构任务

• 欧式结构恢复

        适用条件：摄像机内参数已知，外参数未知

        背景：扫地机器人或者无人驾驶车上，可以预先标定好相机的内参数

• 仿射结构恢复

        适用条件：摄像机为仿射相机，内、外参数均未知

        背景：待重构物体离摄像机较远，待重构物体或者场景深度变化不大（仿射相机参数更少，恢复起来更简洁）

• 透视结构恢复

        适用条件：摄像机为透视相机，内、外参数均未知

        背景：互联网上下载一组图片，不知道相机具体参数

二、欧式结构恢复（摄像机内参数已知，外参数未知）

1. 欧式结构恢复问题

已知：

        \(n\)个3D点\({{X}_{j}}\)在\(m\)张图像中的对应点的像素坐标\({{x}_{ij}}(i=1,...,m,j=1,...,n)\)，且\({{x}_{ij}}={{M}_{i}}{{X}_{j}}={{K}_{i}}\left[ \begin{matrix}   {{R}_{i}} & {{T}_{i}}  \\\end{matrix} \right]{{X}_{j}}(i=1,...,m,j=1,...,n)\)。其中，\({{M}_{i}}\)为第\(i\)张图片对应的摄像机的投影矩阵。

求解：

        \(m\)个摄像机的外参数\({{R}_{i}}\)及\({{T}_{i}}(i=1,...,m)\)；

        \(n\)个三维点\({{X}_{j}}(j=1,...,n)\)的坐标。

2. 欧式结构恢复问题（两视图）

问题：

\(\begin{align}  & {{x}_{1j}}={{M}_{1}}{{X}_{j}}={{K}_{1}}\left[ \begin{matrix}   I & 0  \\\end{matrix} \right]{{X}_{j}} \\  & {{x}_{2j}}={{M}_{2}}{{X}_{j}}={{K}_{2}}\left[ \begin{matrix}   R & T  \\\end{matrix} \right]{{X}_{j}}(j=1,...,n) \\ \end{align}\)

求解：

• 求解基础矩阵\(F\)：归一化八点法
• 利用\(F\)与摄像机内参数求解本质矩阵\(E\)：\(E={{K}_{2}}^{T}F{{K}_{1}}\)

• 分解本质矩阵获得\(R\)与\(T\)：\(E\to R,T\)

• 三角化求解三维点\({{X}_{j}}\)坐标：\({{X}_{j}}^{*}=\underset{{{X}_{j}}}{\mathop{\arg \min }}\,(d({{x}_{1j}},{{M}_{1}}{{X}_{j}})+d({{x}_{2j}},{{M}_{2}}{{X}_{j}}))\)

3. 本质矩阵分解

步骤1：SVD分解→\(E=U\text{diag}(1,1,0){{V}^{T}}\)

步骤2：

\(R=\left[ \det (UW{{V}^{T}}) \right]UW{{V}^{T}}orR=\left[ \det (U{{W}^{T}}{{V}^{T}}) \right]U{{W}^{T}}{{V}^{T}}\)，其中\(W=\left[ \begin{matrix}   0 & -1 & 0  \\   1 & 0 & 0  \\   0 & 0 & 1  \\\end{matrix} \right]\)

\(T=\pm {{u}_{3}}\)（\({{u}_{3}}\)为\(U\)的第三列）

步骤3：

\[\left\{ \begin{matrix}   R=\left[ \det (UW{{V}^{T}}) \right]UW{{V}^{T}},T={{u}_{3}}  \\   R=\left[ \det (UW{{V}^{T}}) \right]UW{{V}^{T}},T=-{{u}_{3}}  \\   R=\left[ \det (U{{W}^{T}}{{V}^{T}}) \right]U{{W}^{T}}{{V}^{T}},T={{u}_{3}}  \\   R=\left[ \det (U{{W}^{T}}{{V}^{T}}) \right]U{{W}^{T}}{{V}^{T}},T=-{{u}_{3}}  \\\end{matrix} \right.\]

注意：

• 选择一个点三角化，正确的一组解能保证该点在两个摄像机的\(z\)坐标均为正。
• 对多个点进行三角化，选择在两个摄像机系下\(z\)坐标均为正的个数最多的那组\(R,T\)，这样比对一个点三角化更鲁棒。

步骤4：通过重建单个或多个点找出正确解

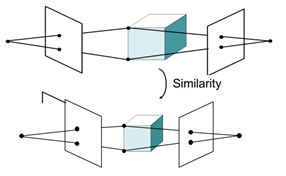
4. 欧式结构恢复的歧义问题

度量重构

• 欧式结构恢复无法估计场景的绝对尺度；
• 恢复出来的欧式结构与真实场景之间相差一个相似变换（旋转，平移，缩放）；
• 恢复的场景与真实场景之间仅存在相似变换的重构称为度量重构。

三、仿射结构恢复（内、外参数均未知）

1. 仿射摄像机模型

        \(x=MX=\left[ \begin{matrix}   {{m}_{1}}  \\   {{m}_{2}}  \\   {{m}_{3}}  \\\end{matrix} \right]X\)，\(M=\left[ \begin{matrix}   {{m}_{1}}  \\   {{m}_{2}}  \\   {{m}_{3}}  \\\end{matrix} \right]=\left[ \begin{matrix}   {{A}_{2\times 3}} & {{b}_{2\times 1}}  \\   {{0}_{1\times 3}} & 1  \\\end{matrix} \right]=\left[ \begin{matrix}   {{m}_{1}}  \\   {{m}_{2}}  \\   \begin{matrix}   0 & 0 & 0 & 1  \\\end{matrix}  \\\end{matrix} \right]\)，

        由于\({{m}_{3}}X=1\)，故\({{x}_{E}}={{({{m}_{1}}X,{{m}_{2}}X)}^{T}}=\left[ \begin{matrix}   A & b  \\\end{matrix} \right]X=\left[ \begin{matrix}   A & b  \\\end{matrix} \right]\left[ \begin{matrix}   x  \\   y  \\   z  \\   1  \\\end{matrix} \right]=A{{X}^{E}}+b\)，

        其中，\({{x}_{E}}\)代表像素点的欧式坐标，\({{X}^{E}}\)代表空间点的欧式坐标。

2. 仿射结构恢复问题

已知：

        \(n\)个3D点\({{X}_{j}}\)在\(m\)张图像中的对应点的像素坐标\({{x}_{ij}}(i=1,...,m,j=1,...,n)\)，且\({{x}_{ij}}={{A}_{i}}{{X}_{j}}+{{b}_{i}}(i=1,...,m,j=1,...,n)\)。其中，\({{A}_{i}},{{b}_{i}}\)组成了第\(i\)张图片对应的仿射摄像机的投影矩阵\({{M}_{i}}=\left[ \begin{matrix}   {{A}_{i}} & {{b}_{i}}  \\   0 & 1  \\\end{matrix} \right]\)。

求解：

        \(m\)个仿射摄像机的投影矩阵\({{A}_{i}},{{b}_{i}}(i=1,...,m)\)；

        \(n\)个三维点\({{X}_{j}}(j=1,...,n)\)的坐标。

仿射结构恢复问题

3. 利用因式分解法求解

        设3D点的质心=世界坐标系的中心。

        首先对图像点中心化，即减去图像点的质心：\({{\hat{x}}_{ij}}={{x}_{ij}}-{{\bar{x}}_{i}}\)，\({{\bar{x}}_{i}}=\frac{1}{n}\sum\limits_{k=1}^{n}{{{x}_{ik}}}\)。

        把去均值以后的\(m\times n\)个测量值写成\(2m\times n\)矩阵的形式：

\[D={{\left[ \begin{matrix}   {{{\hat{x}}}_{11}} & {{{\hat{x}}}_{12}} & \cdots  & {{{\hat{x}}}_{1n}}  \\   {{{\hat{x}}}_{21}} & {{{\hat{x}}}_{22}} & \cdots  & {{{\hat{x}}}_{2n}}  \\   \vdots  & \vdots  & \ddots  & \vdots   \\   {{{\hat{x}}}_{m1}} & {{{\hat{x}}}_{m2}} & \cdots  & {{{\hat{x}}}_{mn}}  \\\end{matrix} \right]}_{2m\times n}}={{\left[ \begin{matrix}   {{A}_{1}}  \\   {{A}_{2}}  \\   \vdots   \\   {{A}_{m}}  \\\end{matrix} \right]}_{2m\times 3}}{{\left[ \begin{matrix}   {{X}_{1}} & {{X}_{2}} & \cdots  & {{X}_{n}}  \\\end{matrix} \right]}_{3\times n}}\]

        其中，\(M={{\left[ \begin{matrix}   {{A}_{1}}  \\   {{A}_{2}}  \\   \vdots   \\   {{A}_{m}}  \\\end{matrix} \right]}_{2m\times 3}}\) ，\(S={{\left[ \begin{matrix}   {{X}_{1}} & {{X}_{2}} & \cdots  & {{X}_{n}}  \\\end{matrix} \right]}_{3\times n}}\)。

        若分解矩阵\(D={{U}_{3}}{{W}_{3}}{{V}_{3}}^{T}\)，则\(M={{U}_{3}},S={{W}_{3}}{{V}_{3}}^{T}\)。

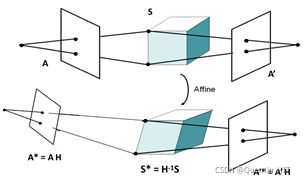
4. 仿射结构恢复歧义

        由于奇异值分解不唯一，通过以下变换可以得到相同的\(D\)：

\[\begin{align}  & {{M}^{*}}=MH \\  & {{S}^{*}}={{H}^{-1}}S \\ \end{align}\]

        其中，\(H\)是任意可逆的3×3矩阵。

仿射结构恢复歧义问题

四、透射结构恢复（内、外参数均未知）

1. 透视结构恢复问题

已知：

        \(n\)个3D点\({{X}_{j}}\)在\(m\)张图像中的对应点的像素坐标\({{x}_{ij}}(i=1,...,m,j=1,...,n)\)，且\({{x}_{ij}}={{M}_{i}}{{X}_{j}}(i=1,...,m,j=1,...,n)\)。其中，\({{M}_{i}}\)为第\(i\)张图片对应的摄像机的投影矩阵。

求解：

        \(m\)个摄像机的投影矩阵\({{M}_{i}}(i=1,...,m)\)；

        \(n\)个三维点\({{X}_{j}}(j=1,...,n)\)的坐标。

透视结构恢复问题

2. 透视结构恢复歧义

        \({{x}_{ij}}={{M}_{i}}{{X}_{j}}=({{M}_{i}}{{H}^{-1}})(H{{X}_{j}})={{M}^{*}}{{X}^{*}}\)，其中，\(H\)是任意可逆的4×4矩阵。

        故透视结构恢复方法只能是在相差一个4×4的可逆变换的情况下恢复摄像机运动与场景结构。

透视结构恢复歧义

3. 代数方法（两视图）

求解：

• 求解基础矩阵\(F\)：归一化八点法

• 利用\(F\)估计摄像机矩阵：\(F\to {{M}_{1}},{{M}_{2}}\)

• 三角化求解三维点\({{X}_{j}}\)坐标：\({{X}_{j}}^{*}=\underset{{{X}_{j}}}{\mathop{\arg \min }}\,(d({{x}_{1j}},{{M}_{1}}{{X}_{j}})+d({{x}_{2j}},{{M}_{2}}{{X}_{j}}))\)

两视图情况

        在已经由归一化八点法算出\(F\)的前提下，假设\(b\)为\({{F}^{T}}\)矩阵最小奇异值的右奇异向量，且\(\left\| b \right\|=1\)，则摄像机矩阵：

\[{{\tilde{M}}_{1}}=\left[ \begin{matrix}   I & 0  \\\end{matrix} \right]\]

\[{{\tilde{M}}_{2}}=\left[ \begin{matrix}   -\left[ {{b}_{\times }} \right]F & b  \\\end{matrix} \right]\]

另外，也可以通过如仿射结构恢复问题中的因式分解法求解。

4. 代数方法（N视图）

N视图情况

         分别对每一个图像对\({{I}_{k}}\)与\({{I}_{h}}\)计算运动与结构：

\[{{I}_{k}},{{I}_{h}}\to {{\tilde{M}}_{k}},{{\tilde{M}}_{h}},{{\tilde{X}}_{[k,h]}}\]

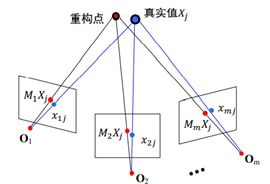
5. 捆绑调整

捆绑调整

        最小化重投影误差：

\[E(M,X)=\sum\limits_{i=1}^{m}{\sum\limits_{j=1}^{n}{D{{({{x}_{ij}},{{M}_{i}}{{X}_{j}})}^{2}}}}\]

        可利用牛顿法或L-M方法求解。

        实际操作中，捆绑调整常用作SFM的最后一步。由于因式分解法和代数法通常存在误差，因此可以将因式分解法和代数法算出的值作为初始解，利用最优化的方法来得到最优解。