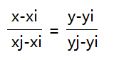Javascript判断点是否在多边型内

射线法Ray-casting Algorithm算法检查点point是否在多边形里面。

用法：insidePolygon([[x1,y1],[x2,y2],[x3,y3]...], [x , y])

参数说明：

polygon多边形坐标集合，格式为[[x1,y1],[x2,y2],[x3,y3]...]。

point 测试点坐标, 格式为[x , y]。

返回true点在内部，false在外部。

下面是javascript代码。

function insidePolygon(polygon, point){

var x = point[0], y = point[1];

var inside = false;

for (var i = 0, j = polygon.length - 1; i < polygon.length; j = i++) {

var xi = polygon[i][0], yi = polygon[i][1];

var xj = polygon[j][0], yj = polygon[j][1];

var intersect = ((yi > y) != (yj > y)) && (x < (xj - xi) * (y - yi) / (yj - yi) + xi);

if (intersect)inside = !inside;

}

return inside;

}

算法解释

1. 函数参数：point 需要判断的点，polygon是多边形顶点集合

伪代码举例：

polygon包含的顺序为A1,A2,A3,A4,A5

polygon=[A1, A2, A3, A4, A5];

A1=[4, 5];

2. For循环遍历每个线段，这里例子是5个线段。

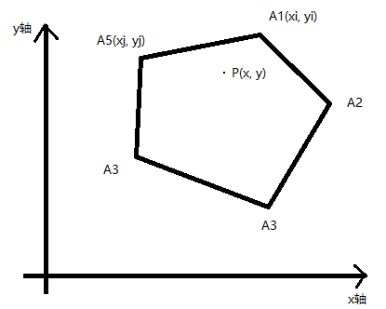
2.1 第一次循环是i=0,j=4;

var xi = polygon[0][0], yi = polygon[0][1];

var xj = polygon[4][0], yj = polygon[4][1];

（图1）

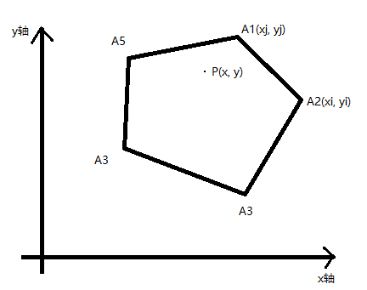
2.2 第二次循环是i=1, j=0;

var xi = polygon[1][0], yi = polygon[1][1];

var xj = polygon[0][0], yj = polygon[0][1];

（图2）

依次类推，直到遍历完。

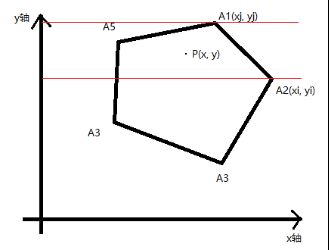
3. (yi > y) != (yj > y))

首选要判断任意点P的y值，是否在图2的A1 A2这个线段的y轴区间内。

如果在yi和yj线段内结果为true,反之false。

4、x < (xj - xi) * (y - yi) / (yj - yi) + xi

4.1引入两点式直线方程:

4.2 推导方程式

(x-xi)/(xj-xi) = (y-yi)/(yj-yi)

=> x-xi = (xj - xi) * (y - yi) / (yj - yi)

=> x = (xj - xi) * (y - yi) / (yj - yi) + xi

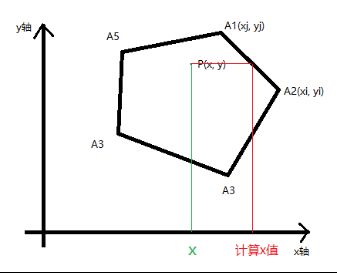
上面的方程式就是求A1A2所构成的直线上，在带入P点的y值后，计算对应的x的值。

绿色的x值为P的实际的x值，计算x值为上面公式推导出的x值。

如果x< 计算x值，说明点在线段的左侧。

5、var intersect = ((yi > y) != (yj > y)) && (x < (xj - xi) * (y - yi) / (yj - yi) + xi)

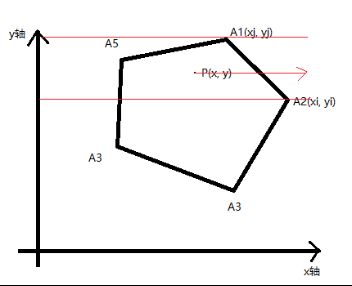
结果为true就说明P点在线段A1A2的左侧，同时在A1A2的y轴区间内。

也就证明，以P点为起点平行于x轴的射线，跟线段A1A2应该有个交点。

6、if (intersect) inside = !inside;

如果有奇数交点,inside =true。

如果有偶数个交点，inside=false