Normalized Mutual information

在写论文做数据测试时有用到一个nmi(normalized mutual information)评价聚类的一种方法，不是很清楚，然后上网找了一下资料。

首先在理解nmi前，先说说mutual information这个东西。
我们先举个例子：

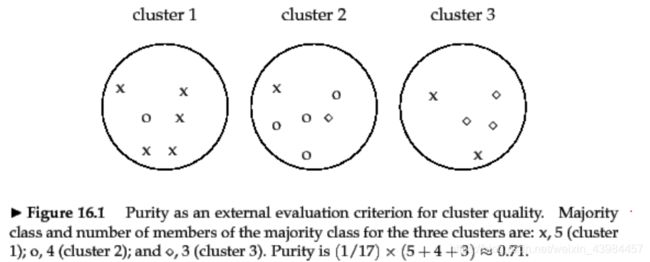
比如说，标准结果是大圆里面的叉叉圈圈点点，上图呢是我们算法聚类出来的结果，那么如何来看我们算法的聚类效果呢，如何计算呢？
我们把上图中的图形用字母来表示出来，集合A是标准的聚类结果，集合B是我们算法的聚类结果，如下：
A:{(aaaaaa),(bbbbbb),(ccccc)}
B:{(aaaaab),(abbbbc),(accca)}
可以按照下列公式来计算：
$I(X,Y)={\sum }_{y\in Y}{\sum }_{x\in X}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$
分子 $p(x,y)$是$x$,$y$的联合分布概率
$p(1,1)=\frac{5}{17}p(1,2)=\frac{1}{17}p(1,3)=0$
$p(2,1)=\frac{1}{17}p(2,2)=\frac{4}{17}p(2,3)=\frac{1}{17}$
$p(3,1)=\frac{2}{17}p(3,2)=0p(3,3,)=\frac{3}{17}$
p(x)是标准集合中字母占比 p(y)是我们算法所得聚类集合中字母的占比。p(x,y)中我们可以把x看作是聚类的序号，把y看作是聚类中叉叉点点圈圈的标记数。也就是对于p(x,y)我们还考虑了叉叉点点圈圈在某一个范围中（某个聚类）占了总数的比例，所以如果x=y，p(x)也不一定等一p(y),因为x和y两个参数的属性是不一样的。
$p(x):$ $p(1)=\frac{6}{17}p(2)=\frac{6}{17}p(3)=\frac{5}{17}$
$p(y):$ $p(1)=\frac{8}{17}p(2)=\frac{5}{17}p(3)=\frac{4}{17}$
这样就可算出MI（mutual information）的值了

nmi(normalized mutual information)公式如下：

$\ast \ast U(X,Y)=2\frac{I(X,Y)}{H(X)+H(Y)}\ast \ast$
其目的是为了让MI的值调整到0到1之间，$H(X),H(Y)$分别为$X,Y$的熵：

$H(X)={\sum }_i^{i=n}p(x_i)I(x_i)={\sum }_i^{i=n}lo{g}_b\frac{1}{p(x_i)}=-{\sum }_i^{i=n}p(x_i)lo{g}_{b}p(x_i)$（$b=2$）

还有一种理解方法，
NMI(A,B)=$2\frac{I(A,B)}{H(A)+H(B)}$，而$I(A,B)$是A，B两向量的MI，H(A)是A的信息熵。

$I(A,B)=H(A)-H(A|B)=H(B)-H(B|A)$;直觉上，如果已知了B的情况，A的信息熵相对于H(A|B)相对于H(A)就要小一点，因为不确定因素变小了嘛。即B能提供给A有用的信息，越有用越相近。

$I(A,B)=H(A)+H(B)-H(A,B)⩾0$,而且当A=B时，H(A,B)=0,I(A,B)最大。此时

$NMIA,B)=2\frac{I(A,B)}{H(A)+H(B)}=2\frac{H(A)}{2H(A)}=1$,故$NMI\in [0,1]$

参考：https://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html