行人重识别论文阅读13-Parameter Sharing Exploration and Hetero-center Triplet Loss for Visible-Thermal Person

Parameter Sharing Exploration and Hetero-center Triplet Loss for Visible-Thermal Person Re-Identification

1. 解决的问题

解决白天可见光和夜晚红外热成像的人员匹配问题，通过使用共享的双流网络进行研究。

VT-ReID问题面临的两个问题：

• 可见光和红外光的图片性质差别较大。
• 由于摄像头视点变化和不同的人体姿势导致的模态内度量困难。

一般此问题都是采用双流的网络解决，将不同模态的特征映射到公共空间中。两个模态的网络不需要相同的架构，但是必须要相同的维度，以便特征嵌入参数共享的网络中。

三重损失由于异常的样例破坏其他学习良好的距离，而且具有高复杂性。

解纠缠方法自动从两个模态的图像中识别ID判别因子。

2. 本文工作

• 探索网络中共享参数部分的比例对模型的影响
• 提出异质中心三元组损失约束模态内和模态间的不同类。

2.1 总结

• 同样使用双流的网络进行模型训练。
• 提出异质中心得三元组损失。
• 模型后面的度量部分很值得深思。
• 提取部分级别特征的方法使用广义的平均池化然后送入到1*1的卷积层。

3. 模型详述

模型分为：1）双流的主干网络 2） 部分特征提取块 3）损失函数：异质中心三元组损失和id softmax损失

3.1 双流主干网络

包括特征提取和特征嵌入。特征提取主要是学习模态特定的特征，特征嵌入是通过将特征映射到公共空间来学习多模态共享的特征。

现有的方法通常使用共享的fc层来计算特征嵌入，但是会出现问题：

• 两个分支包含独立的参数，如果每个分支都有深度网络学习那么参数会变为两倍。
• 特征嵌入包含fc层，只能处理没有人体结构信息的ID形状特征向量。

本文设计CNN模型分为两部分，前半部分可看做双流的特征提取模块，后半部分为特征嵌入模型。

双流的特征提取网络

此处，特征提取网络的表示：${\varphi }_v,{\varphi }_t,{\varphi }_{vt}$分别表示visible，thermal， visible-thermal的特征提取网络。给出一个图片$I_v,I_t$他们经过网络的得到的特征如下：

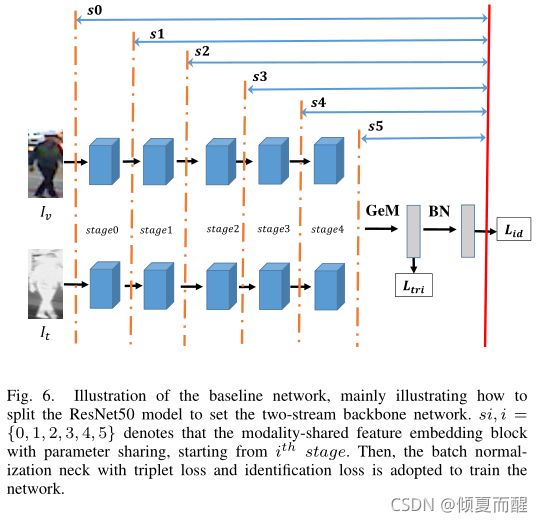
使用ResNet50作为主干网络，网络总共有5个模块，在参数独立和参数共享方面做如下实验：

部分级别的特征提取块：典型的方法是将人划分为水平条带，粗略的提取零件级别的特征，然后将其连结起来描述人的身体结构。也就是说，给定一个人的模态图像，在经里从双流主干网络等所有层之后将变成特征图，基于三维特征图，提取部分级别的特征有三个步骤：

• 在水平方向均匀地划分在顶部stripe中，以生成粗略的身体部位特征图。
• 使用广义平均 GeM替代最大池化或平均池化级啊昂三维部分特征转化为一维部分特征。给定$X\in R^{C\times H\times W}$，GeM可表示为：$\hat{x}=(\frac{1}{\Vert X\Vert }{\sum }_{x_i\in X}{x}_i^p{)}^{\frac{1}{p}}$，其中，$\hat{x}\in R^{C\times 1\times 1}$表示池化后的结果，p是超参数，可以通过反向传播预设或者学习。
• 使用$1\times 1$的Conv块对零件级特征向量进行降维。

每一个部分级别的特征向量采用$L_{hc\_tri}$度量，然后采用全连接层的$softmax{L}_{id}$进行识别。最后将所有部分特征进行连接形成相似度度量的最终特征。

hetro-center 三元组损失：

首先三元组损失：
$$\begin{gathered} L_{bh\_tri}(X)=\stackrel{allanchors}{\sum _{i=1}^P\sum _{a=1}^K}[\rho +\stackrel{hardestpositive}{\underset{p=1...K}{\max }\Vert x_a^i-x_p^i{\Vert }_2}-\stackrel{hardestnegative}{\underset{j=1...P \\ n=1...K \\ j\ne i}{\min }\Vert x_a^i-x_n^j{\Vert }_2}{]}_{+} \end{gathered}$$
使用欧几里得距离和$max\{x,0\}$。

采样策略：首先随机选择P个人，分别选择K张图片，这样就组成了$2\ast P\ast K$张图片，这种采样策略可以充分利用小样本之间的关系。而且通过这种方式，每个类的样本数量相同，可以避免类不平衡引起的扰动。由于随机抽样机制，小批量中的局部约束可以达到与整个集合中的全局约束相同的结果。

此处作者提出改进：提出类中心的概念
$$\begin{gathered} c_v^i=\frac{1}{K}\sum _{j=1}^K{v}_j^i, \\ {c}_t^i=\frac{1}{K}\sum _{j=1}^K{t}_j^i \end{gathered}$$
此处，$v_j^i$表示mini-batch中第i个人的第j张visible图片。

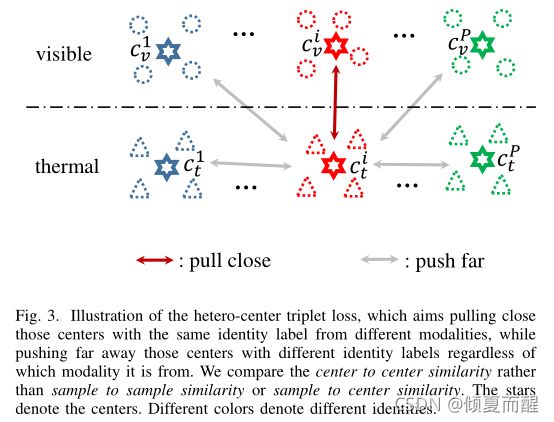
原理可用下图表示：

度量学习的目标是让同类之间彼此靠近，异类之间彼此远离。故hetero-center的三元组损失表达式为：
$$\begin{gathered} L_{hc\_tri}(C)=\sum _{i=1}^P[\rho +\Vert c_v^i-c_t^i{\Vert }_2-\underset{n\in \{v,t\} \\ j\ne i}{\min }\Vert c_v^i-c_n^j{\Vert }_2{]}_{+} \\ +\sum _{i=1}^P[\rho +\Vert c_t^i-c_v^i{\Vert }_2-\underset{n\in \{v,t\} \\ j\ne i}{\min }\Vert c_t^i-c_n^j{\Vert }_2{]}_{+} \end{gathered}$$
对于每一个特征，该损失不仅集中在一个跨模态的正对上，也在模态内和模态间最难挖掘的负对上。

这种方法有两个优点：

1） 降低了计算成本。

–	positive	negative
$L_{bh\_tri}$	$2PK\times (2K-1)$	$2PK\times 2(P-1)K$
$L_{hc\_tri}$	$2P$	$2P\times 2(P-1)$

2. 将基于样本的损失函数退化为基于中心的损失函数，保留在公共空间同时处理可见和红外模态之间变化的特性。对每个特征，最小化模态正中心对距离可以保证类内的紧凑性，最难的负中心挖掘可保证两种模态的可区分性。

与其他中心损失对比：学习中心learned center：通过为每个类预先设置一个中心参数来学习。

计算中心computed center：直接基于所学习的深度特征来计算中心。

The learned centers：首先用于人脸验证，学习每个类中心，并惩罚深度特征与其对应中心之间的距离。
$$L_{lc}=\frac{1}{2}\sum _{i=1}^P\sum _{j=1}^K(\Vert v_j^i-c^i{\Vert }_2+\Vert t_j^i-c^i{\Vert }_2)$$
比较：$L_{hc\_tri}$是在对anchor中心对中心的比较中得到的。$L_{lc}$是sample对中心的比较。

前者计算两个模态的中心。后者将两个中心统一为一个学习向量。

前者挖掘模态内和模态间的属性，后者只关注类内紧凑性。

$L_{hc\_tri}$主要是集中于类间可分离性和类内紧凑性，$L_{lc}$忽略了模态内和模态间的类间可区分性。后者在模态类内紧凑型表现良好，但在跨模态类内紧凑性方面表现比较差。

The computed centers:直接基于所学习的深度特征计算中心。本文也采用这种办法，将中心直接计算为公式，提出hetero-center loss以改善组内交叉模态相似性，惩罚两个模态分部之间的中心距离：
$$L_{hc}=\sum _{i=1}^P\Vert c_v^i-c_t^i{\Vert }_2$$
其不同为：上述的函数侧重于类内交叉模态的紧凑性，本文提出的方法侧重于三元组损失挖掘类内和类间的可分辨性。上述函数是本文所提出的一部分。

损失函数：

id loss被用于通过将每个人视为一个类来整合识别特征信息。采用标签平滑操作防止模型训练过拟合。

N是训练集上特征的个数，$\xi$是训练集中模型的置信度。
$$L_{att}=L_{hc\_tri}^g+\sum _{i=1}^p(L_{id}+\lambda L_{hc\_tri}^i)$$
$\lambda$是预设的权衡参数。

4.实验

4.1 数据集

–	摄像头	训练集	测试集
SYSU-MM01	6(4/2)	395特征（22258/11909）	96特征（3803图片）
RegDB	2(1/1)	412特征（每个摄像头捕获特征的10张图片）

all-search，gallery集合包含所有四个可见摄像头捕获的所有可见光图像

indoor-search，gallery仅包含由两台室内可见光摄像头的可见光图像

all-search比indoor-search更具有挑战性。

RegDB中数据集被随机分为两半，用于训练和测试。测试中，选择一个模态的图像用作图库集，另一个模态作为查询集，重复10次取得平均值。

4.2 评估指标与细节

使用CMC mINP mAP作为评价指标。

框架：pytorch

主干网络：ResNet50

预训练模型：ImageNet，最后一个卷积块stride设置为1(原来为2)以获得具有大尺寸的细粒度特征映射。

训练阶段：resize(288*144) padding 10 随机左右反转 裁剪 动量参数:0.9 学习率：0.1 学习率变化：

预设的边界参数$\rho =0.3,P=6,K=8$.$\lambda =2.0forRegDB,\lambda =1.0forSYSU-MM01$.

部分级特征的维度为256，将特征分为6块 stripes。

4.3 实验对比

结果显而易见。

5. 实验结果

5.1 主干网络的设置

在基于BagTricks上涉及的AGW baseline，从双流主干网络输出的3D特征映射有广义平均池化获得2维的特征向量，然后采用BN层对网络进行训练，首先在2维特征商用三元组损失然后再BN向量上一次使用ID损失。

结果如下所示：

s5：证明没有人空间结构信息的特征不能用来描述行人。

s0：多模态行人重识别问题中人的空间结构信息比颜色信息更重要。

RegDB由双摄像头采集，其中可见光图像和红外图像对齐，SYSU-MM01部署在不同视角的不相交的摄像头采集，可见光和红外光有不同的姿势和视图。SYSU-MM01需要更多特定于模态的层来提取人员空间结构。

s2：获得总体更好的性能。

5.2 部分级特征学习

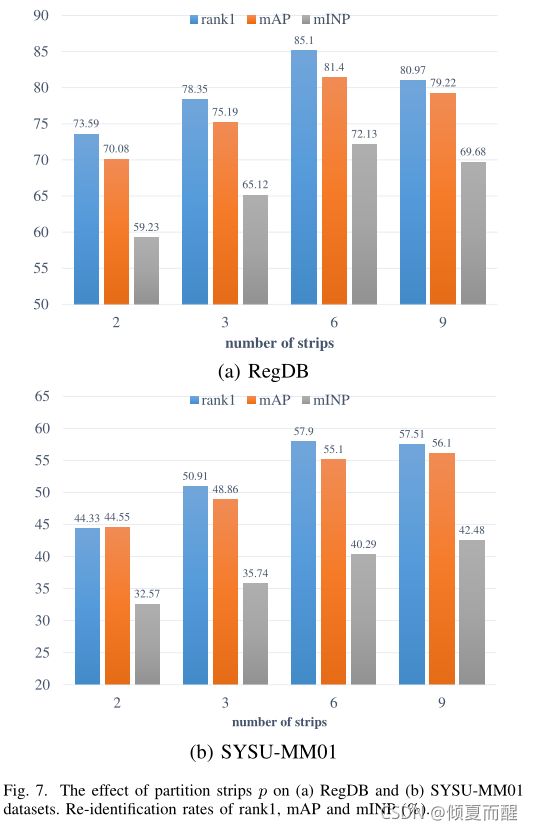
在双流网络和损失层评估层之间添加统一区分策略，此处考虑三个重要的因素：stripe的数量，GeM广义平均池化层，one-by-one的Conv层。

stripe的数量决定了一个人局部特征的粒度。

最大池化的性能优于平均池化的性能，广义平均池化的方法性能最好。

局部特征维度：d=256在绝大部分指标上都比较优秀。

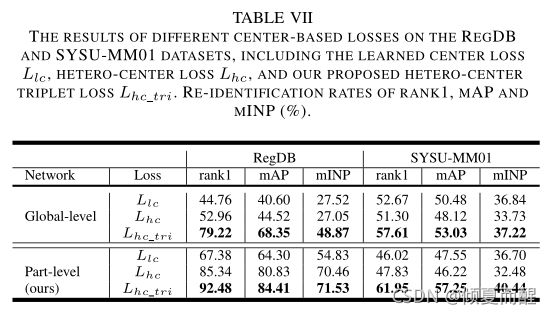
5.3 Hetero-center based triplet loss

与传统的三元组损失进行比较，同时和异质中心的损失进行比较，都显示出比较好的性能。

$L_{hc\_tri}$关注类间分离性和类内的差异性。

$L_{hc}和L_{lc}$只关注类内跨模态紧凑性，忽略了类内和类间模态的类间可分离性。

三个模块同时组合才能获得最好的性能。